LeetCode动态规划训练营(1~5天)
Posted 沉迷单车的追风少年
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode动态规划训练营(1~5天)相关的知识,希望对你有一定的参考价值。
目录
第一天
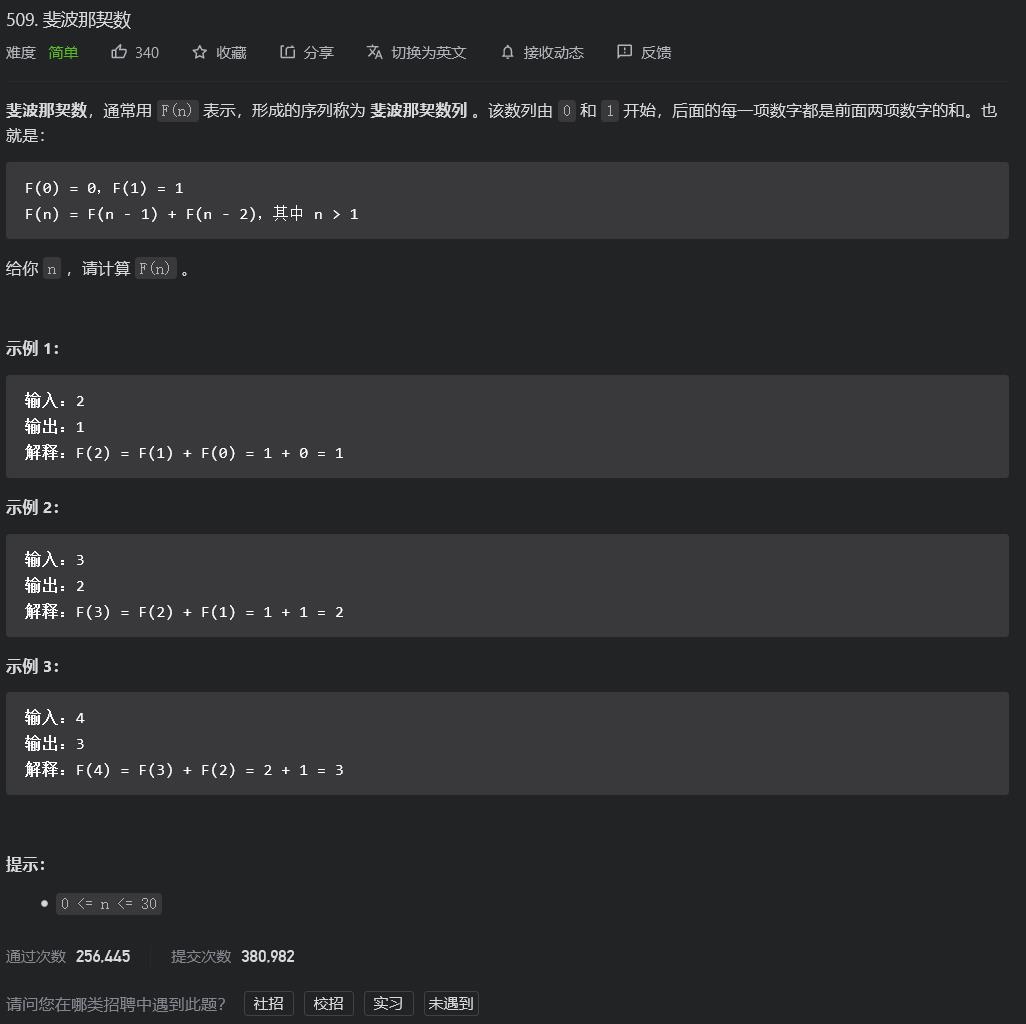
LeetCode509.斐波拉契数
不说了,大一刚开学学会的第一个算法。这波直接回忆童年。
class Solution
public:
int fib(int N)
if(N<=1)
return N;
vector<int> dp(N+1,0);
dp[0] = 0;
dp[1] = 1;
for(int i=2;i<=N;i++)
dp[i] = dp[i-1]+dp[i-2];
return dp[N];
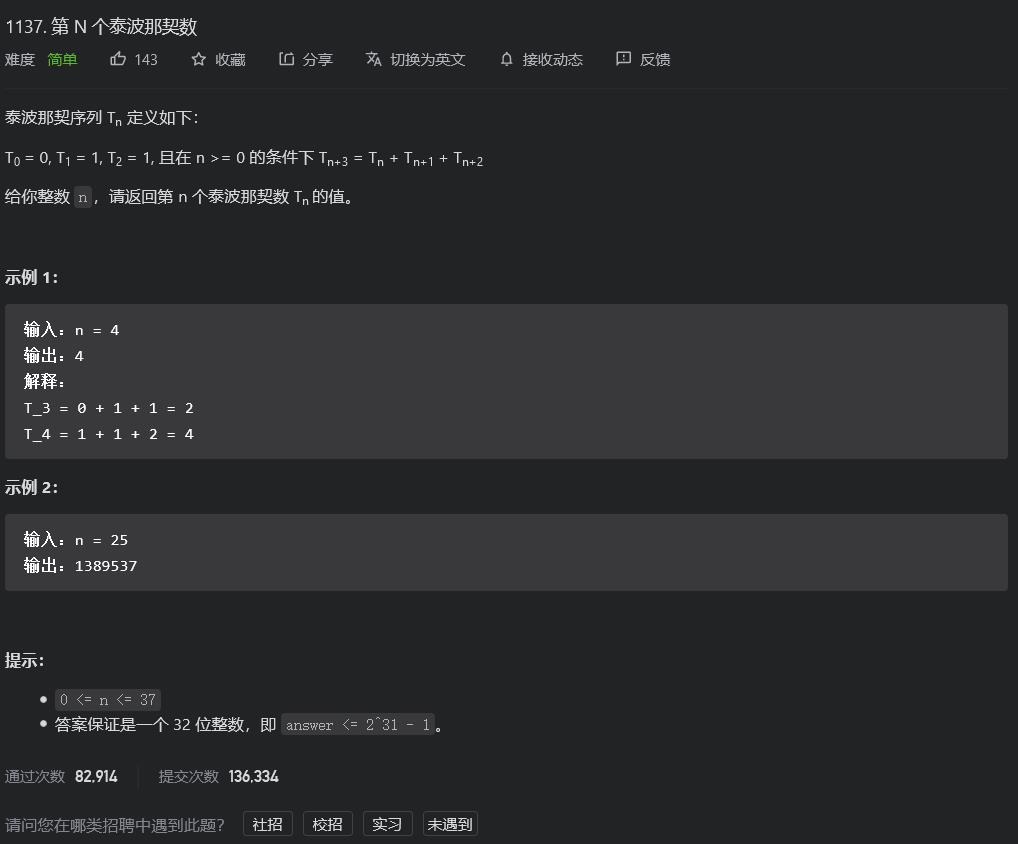
;LeetCode1137.第N个泰波那契数
class Solution
public:
int tribonacci(int n)
int dp[38]=0;
dp[0] = 0;
dp[1] = 1;
dp[2] = 1;
if (n <= 2)
return dp[n];
for (int i = 3; i <= n; i++)
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
return dp[n];
;第二天
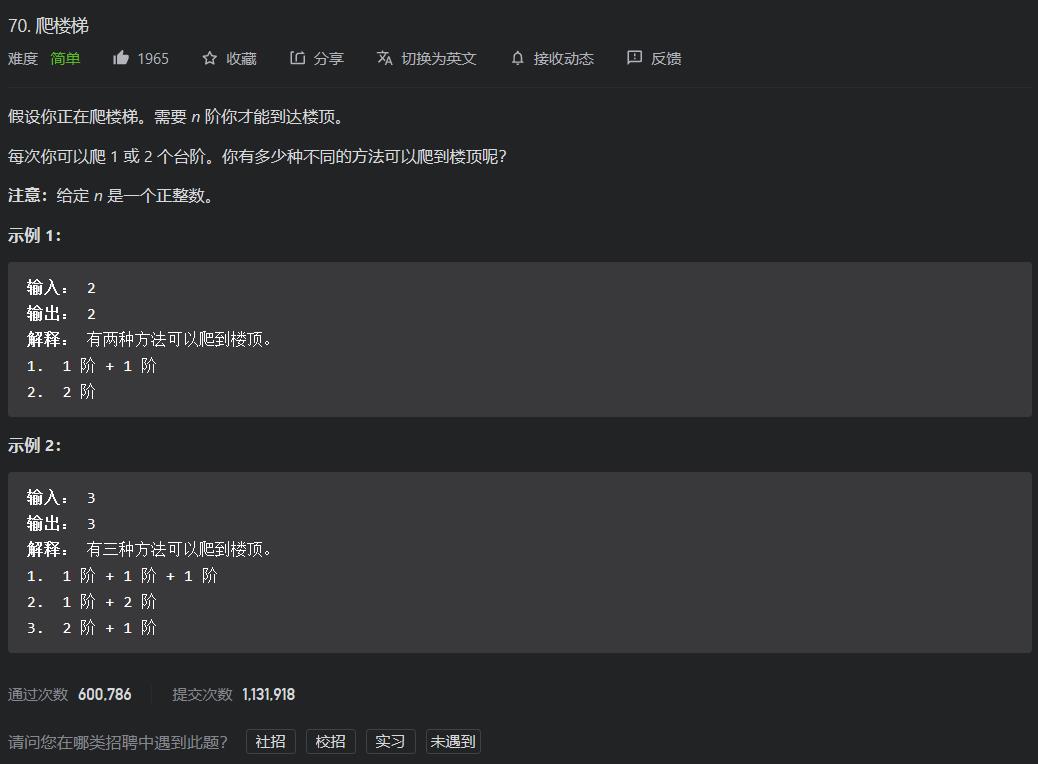
LeetCode.70爬楼梯
超经典,好像也是剑指offer里面的经典
class Solution
public:
int climbStairs(int n)
if(n<=2)
return n;
vector<int> dp(n+1,0);
dp[1] = 1;
dp[2] = 2;
for(int i=3;i<=n;i++)
dp[i] = dp[i-1]+dp[i-2];
return dp[n];
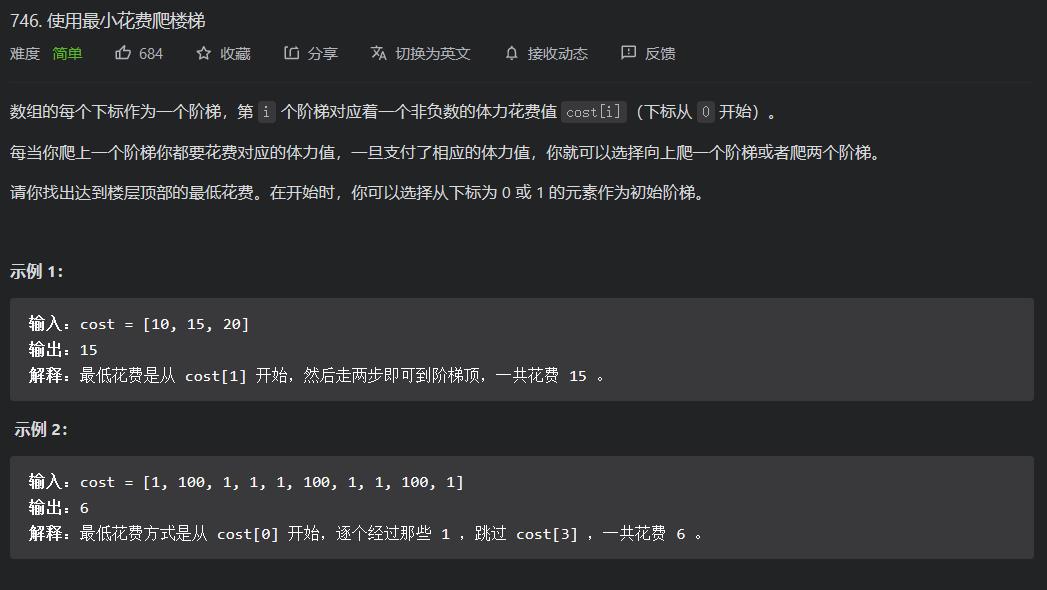
;LeetCode746.使用最小花费爬楼梯
思路是每次从上一个或者上上一个最小的体力值的楼梯上爬上来。dp[i] = (cost[i] + min(dp[i-1], dp[i - 2]))
class Solution
public:
int minCostClimbingStairs(vector<int>& cost)
int N = cost.size();
vector<int> dp(N, 0);
dp[0] = cost[0];
dp[1] = cost[1];
if (cost.size() == 2)
return min(dp[1], dp[0]);
for (int i = 2; i < N; i++)
dp[i] = (cost[i] + min(dp[i-1], dp[i - 2]));
return min(dp[N-1], dp[N-2]);
;第三天
经典入门级DP:LeetCode198.打家劫舍
这道题可以说是LeetCode上最经典,出镜率最高的问题之一,据说字节还叫头条的时候,动不动就出这道题来玩……
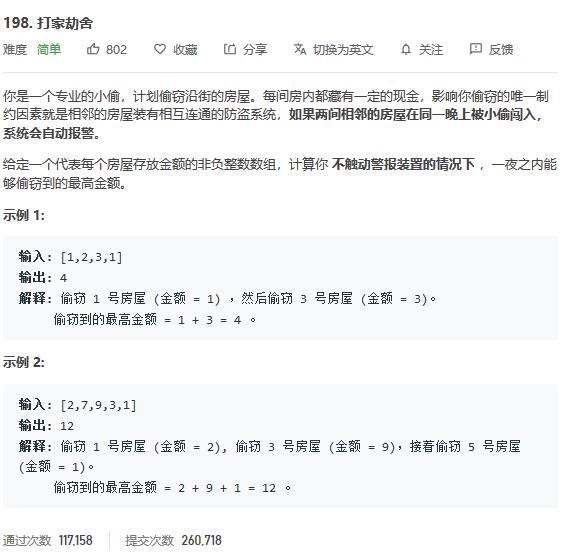
一开始完全没思路,尿了
看热评第一的大佬:

我只能说,大佬牛逼!!!
解释:
假设偷盗经过了第i个房间时,那么有两种可能,偷第i个房间,或不偷第i个房间。如果偷得话,那么第i-1的房间一定是不偷的,所以经过第I个房间的最大值DP(i)=DP(I-2) +nums[i];如果经过第i房间不偷的话,那么经过第i房间时,偷取的最大值就是偷取前i-1房价的最大值。
这两种方案分别是dp[i-2]+nums[i]和 dp[i-1],取最大值就是经过第i房间的最大值。

class Solution
public:
int rob(vector<int>& nums)
if (nums.empty())
return 0;
else if (nums.size() == 1)
return nums[0];
int dp[nums.size()];
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i<nums.size(); i++)
// 要么是上一次打劫(上上一家)得到的综合加上这这家打劫的金额
// 要么是从上面一家开始打劫,之前打劫的不算
dp[i] = max(dp[i-2] + nums[i], dp[i-1]);
return dp[nums.size()-1];
;打家劫舍升级:LeetCode213.打家劫舍II

看似是一个有环问题,但是和链表有环那一类有环问题是完全不一样的。
此处的有环问题可以归类为打劫了第一个就不能打劫最后一个,不打劫第一个就能打劫最后一个。
所以此处的有环问题只用这样化解一个就可以了。
class Solution
public:
int rob(vector<int>& nums)
int N = nums.size();
vector<int> dp1(N, 0); // 打劫第一个
vector<int> dp2(N, 0); // 不打劫第一个
if (nums.empty())
return 0;
if (nums.size() == 1)
return nums[0];
if (nums.size() == 2)
return max(nums[0], nums[1]);
// 分成两段打家劫舍来考虑
// 打劫了第一个就不能打劫倒数第一个
dp1[0] = nums[0];
dp1[1] = max(nums[0], nums[1]);
for (int i = 2; i < N - 1; i++)
dp1[i] = max(dp1[i - 2] + nums[i], dp1[i - 1]);
// 不打劫第一个就能打劫倒数第一个
dp2[0] = 0;
dp2[1] = nums[1];
for (int i = 2; i < N; i++)
dp2[i] = max(dp2[i - 2] + nums[i], dp2[i - 1]);
return max(dp1[N - 2], dp2[N - 1]);
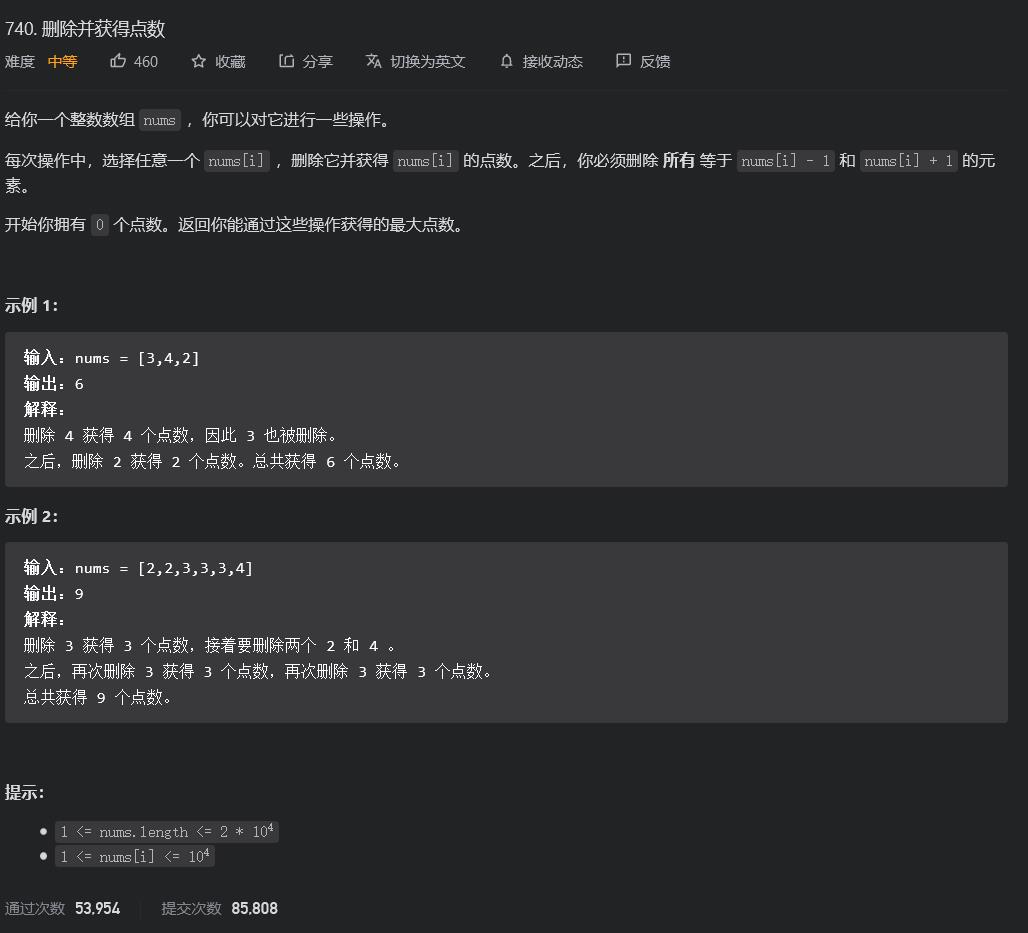
;继续打家劫舍:LeetCode740.删除比获得点数
这道题很牛逼,非常牛逼。
我们要删除的点,就是不能挨在一起删除的问题。这和打家劫舍一模一样:不能打劫相同挨在一起的。
所以我们重新构造一个数组,这个数组存储了每中数字之和。
然后用打家劫舍的思维遍历一遍这个数组就OK,非常牛逼啊这个思路!
class Solution
public:
int deleteAndEarn(vector<int>& nums)
int temp[10001] = 0;
int dp[10001] = 0;
for (auto num : nums)
temp[num] += num;
dp[0] = 0;
dp[1] = temp[1];
for (int i = 2; i < 10001; i++)
dp[i] = max(dp[i - 2] + temp[i], dp[i - 1] );
return dp[10000];
;第四天
LeetCode.55跳跃游戏
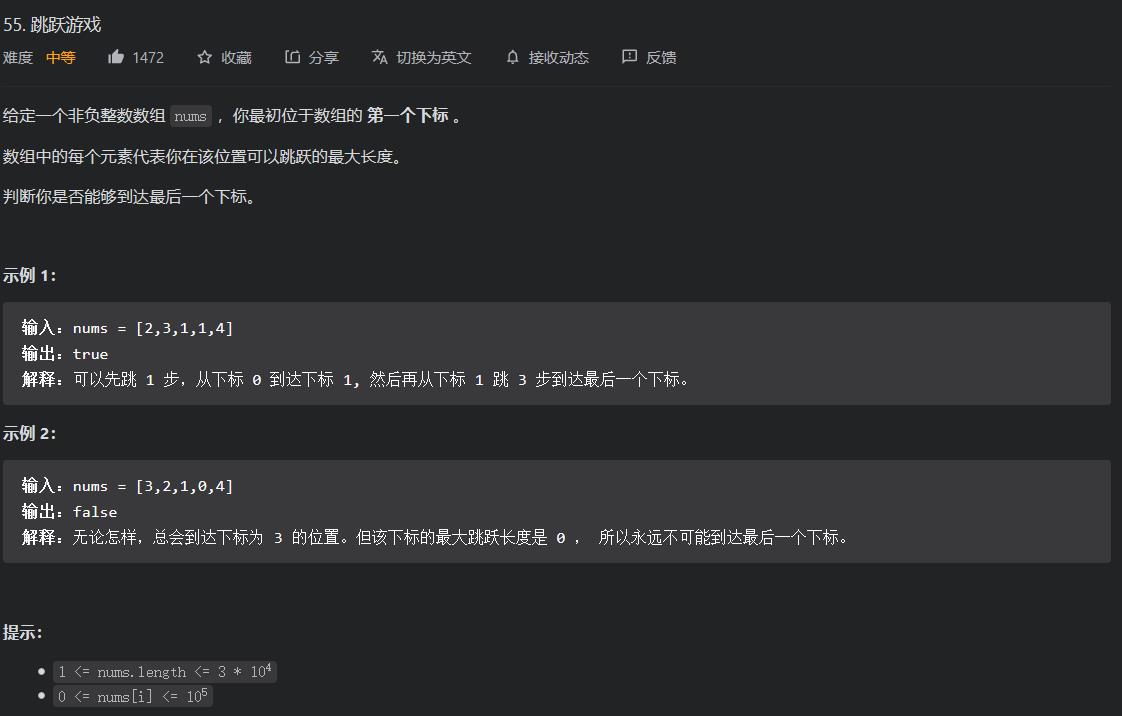
用dp维护一个能跳跃到的最大点的位置坐标即可。
class Solution
public:
bool canJump(vector<int>& nums)
int maxDis = nums[0];
for (int i = 1; i < nums.size(); i++)
if (i <= maxDis)
maxDis = max(maxDis, nums[i] + i);
return maxDis >= nums.size() - 1;
;LeetCode45.跳跃游戏II

以上是关于LeetCode动态规划训练营(1~5天)的主要内容,如果未能解决你的问题,请参考以下文章