论文｜被“玩烂”了的协同过滤加上神经网络怎么搞？

Posted 2022-08-01 搜索与推荐Wiki

相信熟悉推荐系统的同学对于协同过滤（Collaborative Filtering）已经熟悉的不能再熟悉了，我也相信很多人心里在想“这么简单的协同，都2020年了，谁还用呀”。

俗话说得好，人不可貌相，海水不可斗量！CF作为最早的推荐算法，基于CF的改进在学术界和工业界应用的十分广泛，就在之前介绍的一篇论文里，介绍了腾讯实时ItemCF的实现和应用，所以说可千万别小瞧协同过滤了。

本篇论文主要介绍新加坡国立大学在17年发表的论文：Neural Collaborative Filtering（神经网络协同过滤），这篇论文主要介绍的点有：

• 协同过滤优化技巧中矩阵分解（MF）的限制
• 如何基于神经网络优化协同过滤

背景

在信息爆炸时代，推荐系统扮演着及其重要的角色，而且在很多在线服务上也应用的十分广泛，比如：电商网站、内容网站、社会媒体网站等。个性化推荐系统的关键是如何基于用户过去一段时间对物品的行为信息进行建模，最著名的属协同过滤（Collaborative Filtering，CF），在各式各样的CF技术中，矩阵分解（Matrix factorzation，MF）是应用的最广泛的。MF将用户和物品映射到同一个潜在的空间中，用一个潜在的向量特征来表示一个用户或者物品，然后将用户与物品的向量内积来表示用户对物品的喜好。

尽管MF对于协同过滤非常有效，但是通过简单的内积计算会影响MF的效果。例如对于显式反馈的评分预测任务，可以通过合并用户和物品的评分偏差来改善MF的内积计算。对于内积计算操作而言，这可能只是一个很小的改动，但它正向的指出了设计一个更好的、专用的交互方式来对用户和物品的行为进行建模。仅仅使用线性相乘的内积计算不足以捕获复杂的用户交互行为。

尽管现在DNN在推荐中应用的比较广泛，但大多数是用户来进行预测建模，在协同过滤方面，仍基于MF来进行计算。本论文主要是利用神经网络来解决MF在协同过滤中的限制，而且论文基于的是用户的隐式反馈数据，与显式反馈相比，隐式反馈可以更加容易的收集用户数据，但也充满了挑战性，因为无法真实的反馈用户满意程度，而且缺乏一些自然的反馈数据。

本篇论文主要探索了如何基于对充满噪声的隐式反馈数据进行建模，主要贡献有以下三点：

• 提出了一种神经网络架构来对用户和物品的潜在特征进行建模，并为基于神经网络的协同过滤设计了通用的框架NCF
• 证明了MF可以被解释为NCF的一个特例，并利用多层感知器增加NCF模型的高度非线性。
• 基于两个真实的数据集证实了NCF的有效性

基础知识

1、了解隐式反馈数据

用$M、N$表示用户和物品的数目，用$Y\in R^{M\ast N}$表示用户对物品的隐式反馈，如果用户$u$对物品$i$有行为，则$y_{ui}=1$，否则为0。$y_{ui}=1$表示用户与物品之间存在交互，但这并不意味着用户$u$喜欢物品$i$，同样$y_{ui}=0$也不能表示用户$u$不喜欢物品$i$，可能是用户$u$并没有注意到物品$i$。

使用隐式反馈数据的推荐问题被形式化的用来估计用户$u$对物品$i$的得分，继而使用这些得分进行排序。基于模型的方法则认为数据可以通过一个底层模型来描述，通常这个底层模型被抽象的认为是${\hat{y}}_{ui}=f(u,i|\Theta )$，${\hat{y}}_{ui}$表示预测分，$\Theta$表示模型的参数，$f$则表示将模型参数转换为预测分的一个映射。

为了计算模型的参数$\Theta$，现有的一些方法遵循机器学习的规则-优化目标函数。在研究中，主要有两种目标函数：PairWise Loss和PointWise Loss。在PointWise 方式中，通常遵循的是回归框架，即最小化${\hat{y}}_{u,i}、y_{u,i}$之间的误差。为了处理数据缺失的问题，则将未观察到的条目视为负反馈数据或者将观察到的反馈中负面样例作为负反馈数据。PiarWise 则认为观察到的样例（正样本）应该比未观察到的样例（负样本）得分高。因此代替了pointwise中的最小化方式，pairwise优化的目标是最大化观察到的样例（正样本）和未观察到的样例（负样本）。

而本文提出的NCF框架则利用神经网络求解参数$\Theta$，继而来估计${\hat{y}}_{ui}$，支持pointwise 和 pairwise。

关于 pointwise、pairwise、listwise可以参考之前发的一篇文章：怎么理解基于机器学习“四大支柱”划分的学习排序方法

2、矩阵分解（MF）

MF将每个用户和物品的联系用潜在的向量特征来表示，用$p_u$和$q_i$分别表示用户和物品的隐含的向量，MF的计算方式是 $p_u、q_i$的内积，如下所示：
$${\hat{y}}_{ui}=f(u,i|p_u,q_i)=p_u^T{q}_i=\sum _{k=1}^K{p}_{u,k}{q}_{i,k}$$
其中$K$表示隐含向量的长度。

如公式所示，假设用户和物品的每个维度的隐含特征都是彼此独立的，并以相同的权重进行线性组合，则MF是对用户和物品的隐含向量进行双向建模。从这个维度理解，MF可以看作是隐含向量的线性模型。

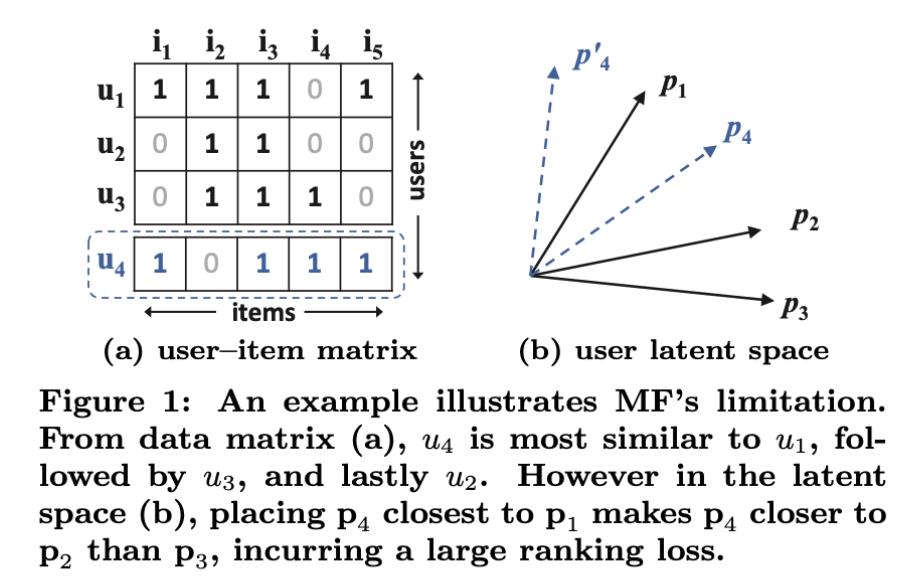
上图展示了MF使用内积进行计算的限制，为了说明示例，有两个限制：

• 使用内积方式或者余弦相似度进行计算时，用户和物品的隐含向量特征维度必须一致
• 使用jaccard相似计算修正计算两个用户的相似度

从上图（a）可以看出，$s_{23}(0.66)>s_{12}(0.5)>s_{13}(0.4)$，即$u_2、u_3$之间的相似度 > $u_1、u_2$之间的相似度 > $u_1、u_3$之间的相似度，可以将他们映射到图（b）所示的空间中，当一个新的用户$u_4$加入比较时，可以很容易的比较两两用户之间的相似度，$s_{41}(0.6)>s_{43}(0.4)>s_{41}(0.2)$，但是如果将$u_4$在图（b）中展示时，会发现和$p_4$最接近的顺序为：$p_1,p_2,p_3$，和我们计算的结果并不一致。

上图说明了，在低维场景下，使用内积方式的限制。一种解决办法是扩大隐含向量的维度，但是会影响模型的泛化能力，而且也会增大计算量。为了解决这个问题，论文中引入了DNN来解决内积方式的局限性。

神经网络协同过滤

1、NCF框架

a. 框架介绍

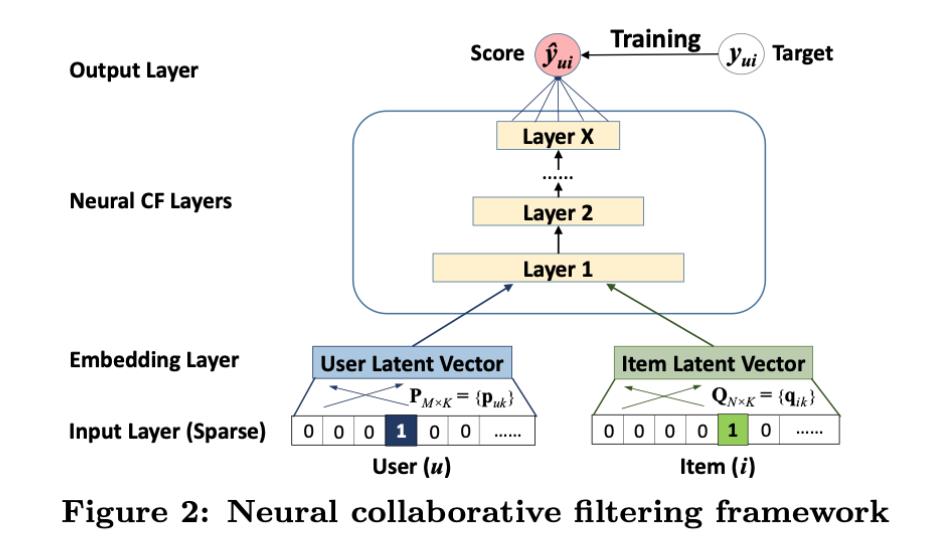
一个通用的NCF框架如上图所示，最下面的input为$v_u^U,v_i^I$表示的是用户和物品的特征向量（这里是进行了ID的onehot编码），同时这里支持进行自定义继而对用户和物品进行建模，比如：上下文、基于内容、最近邻等。这种通用的内容输入，可以轻易的解决新用户的冷启动问题。

Input Layer输入的是稀疏向量，经过Embedding Layer转转化为稠密向量，之后向量被传入到多层的神经网络，这一整块被称为 Neural CF Layers，最后一层称为 Output Layer，输出层的维度决定了模型的功能，输出的${\hat{y}}_{ui}$为预测分值，模型训练的目标是最小化 y ^ u i 、 y u i \\haty_ui、y_ui y^​以上是关于论文｜被“玩烂”了的协同过滤加上神经网络怎么搞？的主要内容，如果未能解决你的问题，请参考以下文章

推荐系统-协同过滤在Spark中的实现

Neural Collaborative Filtering（神经协同过滤）

推荐系统召回策略—基于协同过滤召回

推荐算法论文：Neural Collaborative Filtering

推荐技术基于协同过滤的网络信息推荐技术matlab仿真

隐性反馈行为数据的协同过滤推荐算法