二叉树的递归与迭代遍历

Posted 2022-07-31 却把清梅嗅

本文将针对二叉树中几种常见的遍历方法进行介绍。

遍历方式

前序遍历

前序遍历首先访问根节点，然后遍历左子树，最后遍历右子树。

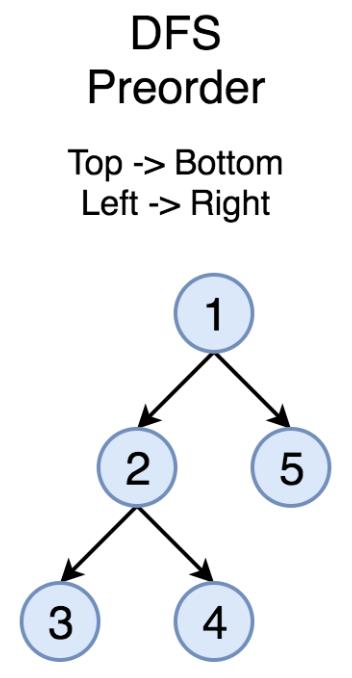
中序遍历

中序遍历是先遍历左子树，然后访问根节点，然后遍历右子树。

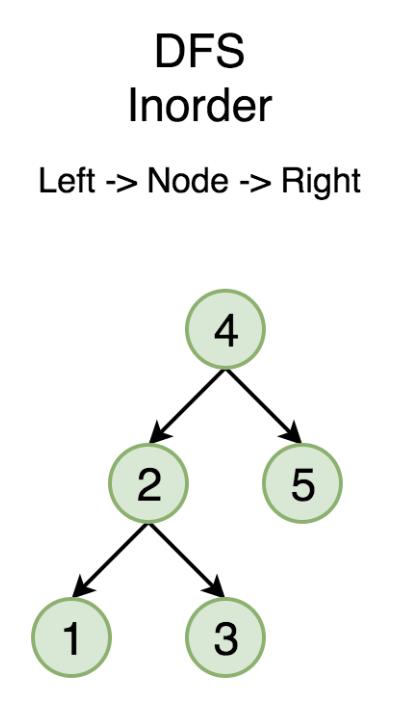
后序遍历

后序遍历是先遍历左子树，然后遍历右子树，最后访问树的根节点。

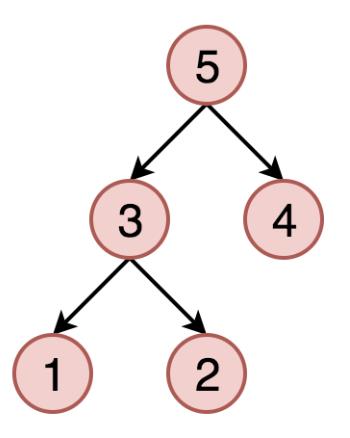
递归实现

递归实现二叉树的遍历是非常简单的，其核心就是 深度优先搜索（DFS） 算法。

由于比较简单，三种遍历方式的实现代码只是 深度优先搜索 过程中执行顺序的区别，故模版如下：

public class Solution 

    // 递归遍历二叉树
    public List<Integer> preorderTraversal(TreeNode root) 
        ArrayList<Integer> list = new ArrayList<>();
        if (root == null) return list;

        dfs(root, list);
        return list;
    

    private void dfs(TreeNode root, ArrayList<Integer> list) 
        if (root == null) return;

        // 前序遍历 根 -> 左 -> 右
        list.add(root.val);     // 根
        dfs(root.left, list);   // 左
        dfs(root.right, list);  // 右

        // 中序遍历 右 -> 根 -> 右
    //    dfs(root.left, list);
    //    list.add(root.val);
    //    dfs(root.right, list);

        // 后序遍历 左 -> 右 -> 根
    //    dfs(node.left, list);
    //    dfs(node.right, list);
    //    list.add(node.val);
    

迭代实现

前序遍历

通过迭代对前序遍历需要一个栈进行辅助，其负责对不同层级父子节点进行迭代存储。

class Solution 
    public List<Integer> preorderTraversal(TreeNode root) 
      ArrayList<Integer> list = new ArrayList<>();
      Stack<TreeNode> stack = new Stack<>();

      TreeNode curr = root;

      // 1.退出最外层迭代的条件是，指针指向null，且栈为空
      while (curr != null || !stack.isEmpty()) 
          // 2.内层循环按顺序入栈，同时更新当前指针
          // 4.这时候也可能是开始遍历右节点
          while (curr != null) 
              stack.push(curr);
              list.add(curr.val);
              curr = curr.left;
          
          // 3.返回父节点，并将指针指向右节点
          curr = stack.pop();
          curr = curr.right;
      

      return list;
    

中序遍历

中序遍历和前序遍历思想是一致的，区别仅仅在于根节点在左叶子节点添加之后添加：

class Solution 
    public List<Integer> preorderTraversal(TreeNode root) 
      List<Integer> list = new ArrayList<>();
      Stack<TreeNode> stack = new Stack<>();

      TreeNode curr = root;

      // 1.退出最外层迭代的条件是，指针指向null，且栈为空
      while (!stack.isEmpty() || curr != null) 
          // 2.内层循环按顺序入栈，同时更新当前指针
          // 5.这时候也可能是开始遍历右节点
          while (curr != null) 
              stack.push(curr.left);
              curr = curr.left;
          
          // 3.返回父节点，并加入数组中
          curr = stack.pop();
          list.add(curr.val);
          // 4.将指针指向右节点
          curr = curr.right;
      
      return list;
    

后序遍历

后序遍历 LeetCode 官方题解给出了一个额外的思路，对于树的 后序遍历 而言，其遍历顺序与 广度优先搜索（BFS） 恰恰是相反的：

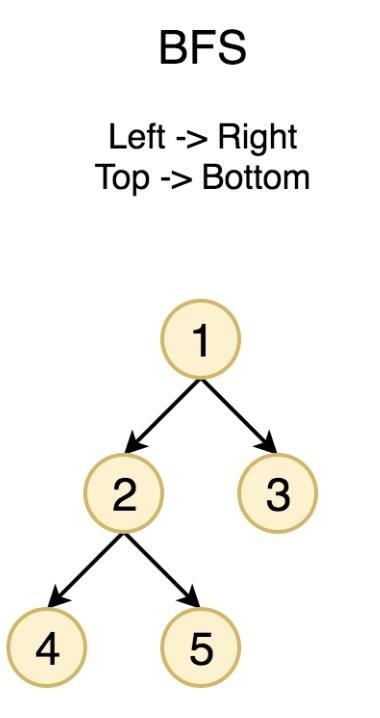
如图所示，BFS的遍历顺序是 1->2->3->4->5，而相同的树后序遍历顺序则是 4->5->2->3->1。

因此，后序遍历的思路如下：

从根节点开始依次迭代，弹出栈顶元素输出到输出列表中，然后依次压入它的所有孩子节点，按照从上到下、从左至右的顺序依次压入栈中。

因为深度优先搜索后序遍历的顺序是从下到上、从左至右，所以需要将输出列表逆序输出。

/**
 * Definition for a binary tree node.
 * public class TreeNode 
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x)  val = x; 
 * 
 */
class Solution 
    public List<Integer> postorderTraversal(TreeNode root) 
        LinkedList<Integer> output = new LinkedList<>();
        // 和传统的bfs不同，这里并没有用 Queue
        // 因为顺序是相反的，这里并不是取第一个元素，而是取栈顶的元素（即同层级节点从右->左遍历）
        Stack<TreeNode> stack = new Stack<>();

        if (root == null) return output;

        stack.push(root);

        while(!stack.isEmpty()) 
           TreeNode node = stack.pop();
           output.addFirst(node.val);

           if (node.left != null) 
               stack.push(node.left);
           
           if (node.right != null) 
               stack.push(node.right);
           
        
        return output;
    

参考 & 感谢

文章绝大部分内容节选自LeetCode，概述：

• https://leetcode-cn.com/explore/learn/card/data-structure-binary-tree/2/traverse-a-tree/7/

例题：

• https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
• https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
• https://leetcode-cn.com/problems/binary-tree-postorder-traversal/

关于我

Hello，我是 却把清梅嗅 ，如果您觉得文章对您有价值，欢迎 ❤️，也欢迎关注我的 博客 或者 GitHub。

如果您觉得文章还差了那么点东西，也请通过关注督促我写出更好的文章——万一哪天我进步了呢？

• 我的Android学习体系
• 关于文章纠错
• 关于知识付费
• 关于《反思》系列