运用递归解决二叉树相关问题

Posted 2022-07-31 却把清梅嗅

在之前的章节中，我们已经介绍了如何解决树的遍历问题。我们也已经尝试过使用递归解决树的为 前序遍历 、 中序遍历 和 后序遍历 问题。

事实上，递归 是解决树相关问题的最有效和最常用的方法之一。本节中，我们将会介绍两种典型的递归方法。

解决方案

本小节内容节选自 LeetCode：运用递归解决树的问题 .

递归是解决树的相关问题最有效和最常用的方法之一。

我们知道，树可以以递归的方式定义为一个节点（根节点），它包括一个值和一个指向其他节点指针的列表。 递归是树的特性之一。 因此，许多树问题可以通过递归的方式来解决。 对于每个递归层级，我们只能关注单个节点内的问题，并通过递归调用函数来解决其子节点问题。

通常，我们可以通过 自顶向下 或 自底向上 的递归来解决树问题。

“自顶向下” 的解决方案

自顶向下 意味着在每个递归层级，我们将首先访问节点来计算一些值，并在递归调用函数时将这些值传递到子节点。 所以 自顶向下 的解决方案可以被认为是一种 前序遍历。 具体来说，递归函数 top_down(root, params) 的原理是这样的：

• 1、在null值的情况下返回指定的值；
• 2、如果有必要，更新answer;
• 3、left_ans = top_down(root.left, left_params)；
• 4、right_ans = top_down(root.right, right_params)；
• 5、如果有必要返回answer。

“自底向上” 的解决方案

自底向上 是另一种递归方法。 在每个递归层次上，我们首先对所有子节点递归地调用函数，然后根据返回值和根节点本身的值得到答案。 这个过程可以看作是 后序遍历 的一种。 通常， 自底向上 的递归函数 bottom_up(root) 为如下所示：

• 1、在null值的情况下返回指定的值；
• 2、left_ans = top_down(root.left, left_params)；
• 3、right_ans = top_down(root.right, right_params)；
• 4、返回answer。

例题

1、二叉树的最大深度

题目描述

解题思路及实现

1、自顶向下

class Solution 
  private int answer = 0;

  public int maxDepth(TreeNode root) 
      max_depth(root, 0);
      return answer;
  

  private void max_depth(TreeNode root, int depth) 
      if (root == null) return;

      if (root.left == null && root.right == null) 
          answer = Math.max(depth, answer);
          return;
      

      max_depth(root.left, depth + 1);
      max_depth(root.right, depth + 1);
  

2、自底向上

class Solution 

  public int maxDepth(TreeNode root) 
      return max_depth2(root);
  

  private int max_depth2(TreeNode root) 
      if (root == null)
          return 0;

      int leftDepth = max_depth2(root.left) + 1;
      int rightDepth = max_depth2(root.right) + 1;
      return Math.max(leftDepth, rightDepth);
  

2、对称二叉树

题目描述

解题思路及实现

这道题笔者的思路是迭代，后来发现非常困难，看了题解才发现，将同一个树作为2次参数分别放入递归函数进行递归，确实是一个很棒的思路。

class Solution 

    public boolean isSymmetric(TreeNode root) 
        return isMirror(root, root);
    

    private boolean isMirror(TreeNode t1, TreeNode t2) 
        if (t1 == null && t2 == null) return true;
        if (t1 == null || t2 == null) return false;

        return t1.val == t2.val && isMirror(t1.left, t2.right) && isMirror(t1.right, t2.left);
    

3、路径总和

题目描述

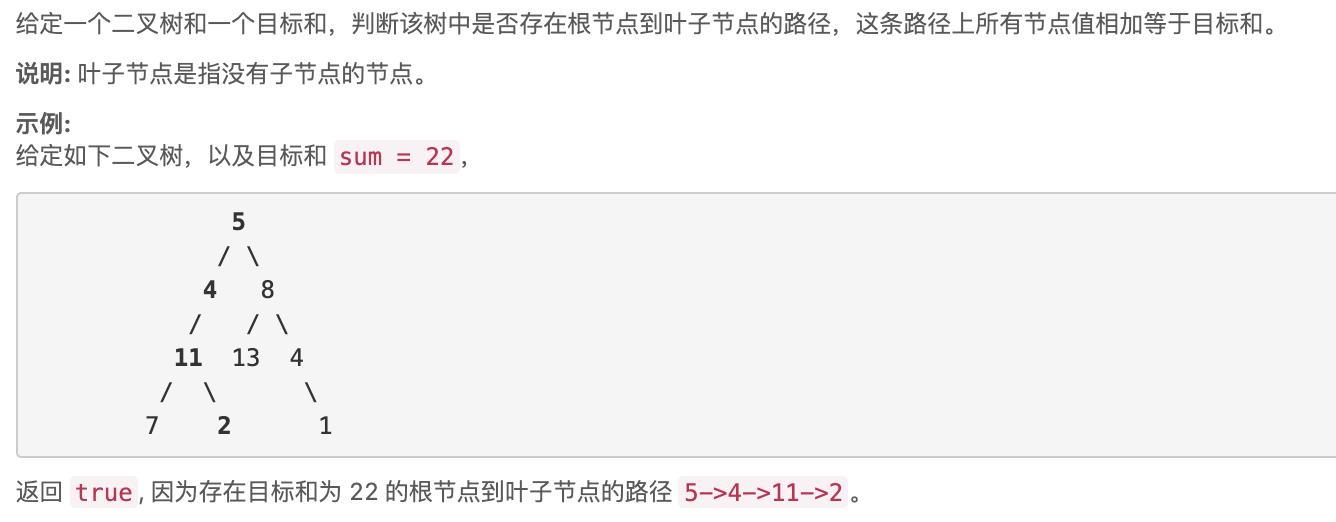
解题思路及实现

比较简单，标准的dfs进行递归：

class Solution 

  public boolean hasPathSum(TreeNode root, int sum) 
      return dfs(root, 0, sum);
  

  private boolean dfs(TreeNode root, int currentSum, int target) 
      if (root == null) 
          return false;
      
      int sum = currentSum + root.val;

      if (root.left != null || root.right != null) 
          return dfs(root.left, sum, target) || dfs(root.right, sum, target);
       else 
          return sum == target;
      
  

参考 & 感谢

文章绝大部分内容节选自LeetCode，概述：

• https://leetcode-cn.com/explore/learn/card/data-structure-binary-tree/3/solve-problems-recursively/11/

例题：

• https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
• https://leetcode-cn.com/problems/symmetric-tree/
• https://leetcode-cn.com/problems/path-sum/

关于我

Hello，我是 却把清梅嗅 ，如果您觉得文章对您有价值，欢迎 ❤️，也欢迎关注我的 博客 或者 GitHub。

如果您觉得文章还差了那么点东西，也请通过关注督促我写出更好的文章——万一哪天我进步了呢？

• 我的Android学习体系
• 关于文章纠错
• 关于知识付费
• 关于《反思》系列