无损压缩经典算法
Posted Mr_厚厚
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了无损压缩经典算法相关的知识,希望对你有一定的参考价值。
@前言
总结经典的文件压缩算法原理,主要包括:哈夫曼压缩算法及其延伸,LZ77算法及其演变算法,LZ78算法及其演变算法,几何编码算法Arithmetic Coding。
1.进行文件压缩的必要性
像图片、声音、视频这些类型的多媒体数据要比文本数据占用多得多的内存空间,尤其是视频文件,文件传输时占用带宽大,存储又占用大量的硬盘空间。
举个例子:一个1080p分辨率格式下90分钟的无压缩视频要多大?
1帧大小 = 1920 x 1080 x 3 = 6220800 bytes (1920x1080是每一帧的像素数,3指的是每个像素红绿蓝三个通道各占一个字节0~256)
***每秒大小 = 6220800 x 25 = 155.52MB!***(假设帧率为每秒25帧,很小了!)
每分钟大小 = 155.52MB x 60 = 9.3312GB!
90分钟:大约839.81GB
存储高清视频的蓝光光碟容量不过只有大约50GB,所以视频如果不压缩根本没法存储,更不用说互相传送了。
2.简单黑白图像的压缩
假设黑白图像的数据如下图,黑色像素用1编码,白色图像用0编码:

黑白图像的尺寸为16x8 = 128,因此需要128bits来表示它。
如果我们从0开始算起,只保存一些列0和1的个数,那么上面的图像信息可以表示为:
21 6 9 1 5 2 8 1 3 2 1 1 8 1 2 2 2 1 8 6 21
其中最大的数字是21,所以可以统一使用5bits(2^5=32)来表示每一个数字,那么现在的存储空间变为5x21=105bits,节省了23bits。
3.字符串行程编码
和上面黑白图像压缩一样的道理,这里压缩一段字符串:RRRRRGGGBBBBBRRRRGB
压缩的结果为:5R3G5B4R1G1B
这种方法叫做行程编码run-ength encoding(RLE),应用于像BMP,TIFF格式的图像文件中。
但这种压缩编码方式很有局限性,我们无法继续用相同的方法进一步压缩压缩后的数据,比如上面的压缩结果无法继续用这种方法压缩,这种压缩基于数据的重复性。
4.信息的可压缩性-信息量和信息熵
信息量
数据的压缩水平和数据的信息量有关,信息量越大自然数据量越大越难以压缩。数据的信息量如何来衡量呢?
例子:假设有一个64位的字符串,64个数字,其中63个0,另一个是1,1可能出现在任意位置,也就是在某个位置的概率为1/64。现在从左往右读取知道找到1。(注意下表是找到1之前的概率,当找到1之后,之后的符号确定不可能再出现1了,因此P(bi=1)变为0,P(bi=0)变为1)
对于在位置i的符号bi,bi为0或者为1的概率分布如下:

事实上,一个符号的概率越大,那么它包含的信息就越小,也就是信息量和符号出现的概率成反比,信息量的定义为:
h
(
x
)
=
l
o
g
2
1
p
(
x
)
h(x)=log_2\\frac1p(x)
h(x)=log2p(x)1
计算对应的符号信息量表:

信息量计算:如果1位于第4个位置:000100…0,则总的信息量为:
Sum = 0.0227 + 0.023 + 0.0235 + 5.9307 = 6
通用公式:
∑ n = 1 i h ( b n ) = ( ∑ m = 66 − i 64 l o g 2 m m − 1 + l o g 2 1 1 / ( 65 − 1 ) ) = l o g 2 ( ( ∏ m = 66 − i 64 m m − 1 ) ( 65 − i ) ) = 6 \\sum_n=1^ih(b_n)=(\\sum_m=66-i^64log_2\\fracmm-1 +log_2\\frac11/(65-1)) = log_2((\\prod_m=66-i^64\\fracmm-1) (65-i)) = 6 n=1∑ih(bn)=(m=66−i∑64log2m−1m+log21/(65−1)1)=log2((m=66−i∏64m−1m)(65−i))=6
每个字符信息量的和表示了整个字符串的信息量,这里至少需要6位来表示这个字符串,要保存的是公式中的索引(0~63)。
信息熵
数据的压缩实际是用更短的数据来表示反复出现的数据实现压缩,因此数据重复率越高或者可预测性越强可压缩性就越高,不同数据可压缩的程度不一样,信息熵是用来衡量数据可压缩的程度的一个参数,计算信息最短的长度的期望,关于信息熵:http://www.ruanyifeng.com/blog/2014/09/information-entropy.html
上面能精确计算信息量是因为我们知道了字符串的具体结构,对于未知的信息我们只能根据概率计算其信息量的期望,计算公式为:
H ( X ) = ∑ i P ( x i ) h ( x i ) H(X) = \\sum_iP(x_i)h(x_i) H(X)=i∑P(xi)h(xi)
最差的情况是当所有符号的概率都相同,概率均匀分布,此时信息熵为最大值,因为对于一个子串,根本无法预测下一个符号。
5.对编码算法的要求
- 通过编码后的编码必须可以准确解码,编码必须确定地对应一种原码;
- 编码算法得到的编码要容易解码,可以很容易的找到信息的末尾,可以在线解码,可以直接对编码进行解码而不用知道完整的编码信息;
- 编码必须是压缩的,否则失去了编码的意义;
6.哈夫曼编码
哈夫曼编码是David A. Huffman于1952年发明的一种满足上面对编码算法要求的一种编码算法。
举一个例子:知道一段字符串全部由a,b,c,d,e五个字母组成,已知了每个字母出现的频率:
a(0.25),b(0.25),c(0.2),d(0.15),e(0.15)
【如果不考虑编码算法,使用定长的编码来区别五个字母,不利用频率这些信息,那么五个字母每个字母需要用3bits表示(22=4,23=8).】
哈夫曼算法是利用频率信息构造一棵二叉树,频率高的离根节点近(编码长度短),频率低的离根节点远(编码长度长),手动构造方法是先将字母按照频率从小到大排序,然后不断选择当前还没有父节点的节点中权值最小的两个,构造新的父节点,父节点的值为这两个节点值的和,直到构造成一棵二叉树,上面的例子构造的Y一棵哈弗曼树如下(由于构造过程中叶子节点的值以及新节点的值可能会相同,所以哈弗曼树的结构不唯一):
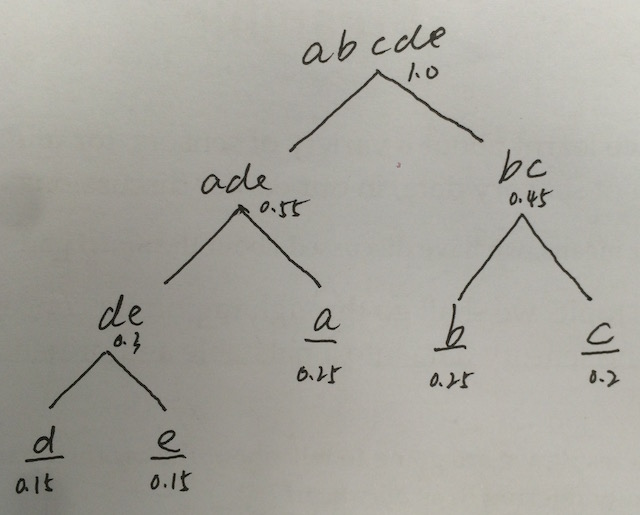
对构造的哈弗曼二叉树进行编码,左边为0,右边为1,就得到一个编码的哈弗曼树,从而对字符串进行编码。
哈夫曼算法C++实现,使用线性数组存储节点的方式实现,输入上面每个字母的权值可以得到哈弗曼树结构:
#include <iostream>
using namespace std;
#define n 5 // 字符个数(叶子个数)
#define m 2*(n)-1 // 总节点数:1+2+4+8+...+n
typedef struct
double weight; // 节点权重
int lchild; // 左子树
int rchild; // 右子树
int parent; // 父节点
HTNODE;
typedef HTNODE HuffmanT[m]; // 一棵线性结构存储的哈弗曼树
/**
* 哈弗曼树初始化
*/
void InitHT(HuffmanT T)
for(int i=0; i<m; i++)
T[i].lchild=-1;
T[i].rchild=-1;
T[i].parent=-1;
// 依次输入每个节点的权重
for(int i=0; i<n; i++)
std::cin>>T[i].weight;
/**
* 找出还没有父节点的节点中权值最小的两个,p1和p2是要选出的权值最小的两个节点的下标,n1是新父节点的下标
*/
void SelectMin(HuffmanT T, int n1, int &p1, int &p2)
int i, j;
// 先任意找两个没有父节点的节点
for(i=0; i<n1; i++)
if(T[i].parent==-1)
p1=i;
break;
for(j=i+1; j<n1;j++)
if(T[j].parent==-1)
p2=j;
break;
// 搜索替换成权值最小的节点
for(i=0; i<n1; i++)
if((T[p1].weight>T[i].weight) && (T[i].parent==-1) && (p2!=i))
p1=i;
for(i=0; i<n1; i++)
if((T[p2].weight>T[i].weight) && (T[i].parent==-1) && (p1!=i))
p2=i;
/**
* 构造哈弗曼树
*/
void CreatHT(HuffmanT T)
int i, p1, p2;
InitHT(T);
// 非叶子节点
for(i=n; i<m; i++)
// 找出还没有父节点的节点中权值最小的两个
SelectMin(T, i, p1, p2);
T[p1].parent=T[p2].parent=i;
T[i].lchild=p1;
T[i].rchild=p2;
T[i].weight=T[p1].weight+T[p2].weight;
/**
* 打印哈弗曼树
*/
void printHT(HuffmanT T)
for(int i=0; i<m; i++)
std::cout<<T[i].weight<<'\\t'<<T[i].parent<<'\\t'<<T[i].rchild<<'\\t'<<T[i].lchild<<std::endl;
/**
* 前台测试
*/
int main()
HuffmanT T;
CreatHT(T);
printHT(T);
return 0;
缩减的哈夫曼算法
哈夫曼编码的缩减实质是对编码字符分组继续进行子分组内编码。先将所有字符按照出现的概率排序,将概率相近的字符作为一个整体参与上一级的编码,这样上一级的编码数量大大减少,分组内继续进行内部哈夫曼编码,同时在上一级中本组的编码作为组内编码的一个固定的前缀。
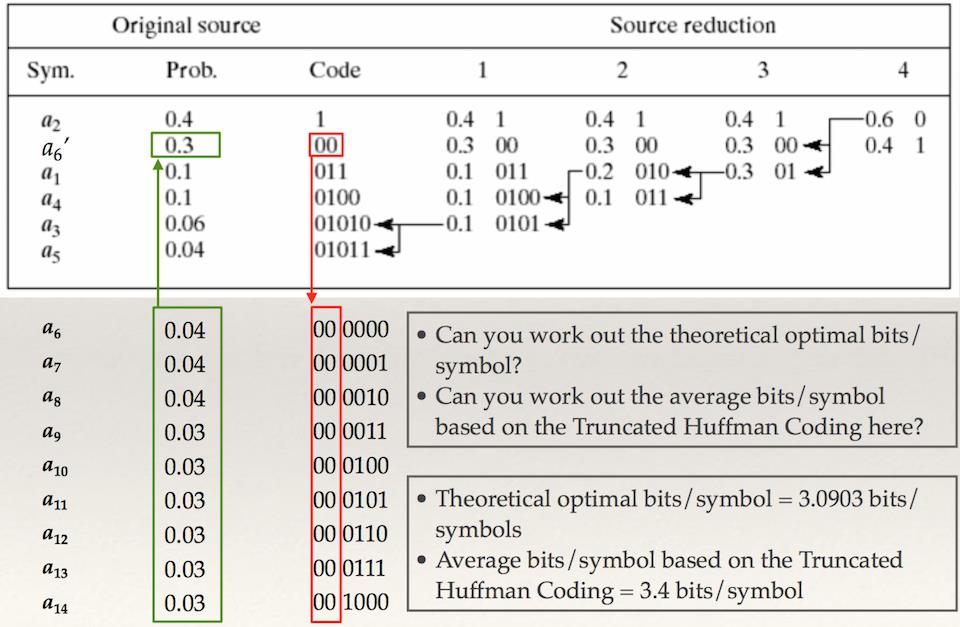
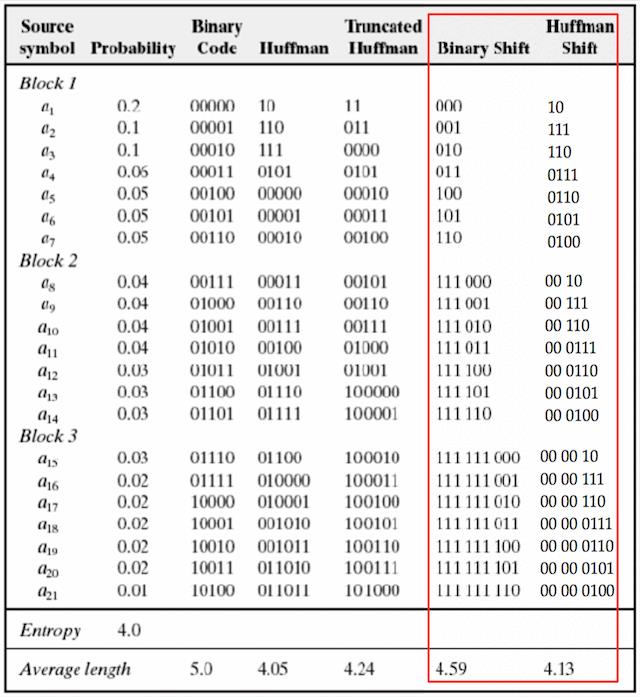
Shift Coding
和缩减的思想类似,将字符按照频率8个一组分块,每到下一块在前面加111进行区分后继续进行3bit的编码。
7.Lempel-Ziv压缩算法
LZ算法及其衍生变形算法是压缩算法的一个系列。LZ77和LZ78算法分别在1977年和1978年被创造出来。虽然他们名字差不多,但是算法方法完全不同。这一系列算法主要适用于字母数量有限的信息,比如文字、源码等。流行的GIF和PNG格式的图像,使用颜色数量有限的颜色空间,其压缩就采用了两种算法的灵活变形应用。
LZ77:
推荐阅读文章:
LZ77算法的思想是在编码解码过程中,使用之前刚结束编解码的部分数据的位置索引来代替当前要编解码的数据,压缩的实现靠的是之前编解码结束的部分数据和当前数据的重复性。
算法中几个重要的对象概念:
LAB(look-ahead-buffer):将要编码的固定长度的数据缓冲;
SB(search-buffer):刚过去的固定长度的数据缓冲,搜索缓冲区,也就是临时的数据字典,要从这里面搜索重复数据获得压缩索引;
Cursor:一个指针,指的是SB和LAB缓冲之间的边界处
**Token(p,l,c)**编码的结果:
- p: 第一个数字指的是SB中开始匹配的位置,注意是从Cursor往前倒着数,从1开始数;
- l: 第二个数字指的是匹配成功的字符个数;
- c: 第三个指的是LAB中匹配结束的下一个字符;
***注意:***在匹配时是搜索字典中最长的匹配,且当前的LAB区域如果继续匹配也继续搜索(比如匹配到SB的最后一个字符后下一个到LAB的第一个字符仍然匹配则继续,直到不匹配或匹配数达到了LAB的长度限制则停止。如果在SB中一个都不匹配则不继续搜索,排除LAB第一个字符自身无尽循环匹配的情况)。
示例:
字符串“aacaacabcabaaac”的一个LZ77编码示例,其中缓冲长度分别为:LAB=4,SB=6
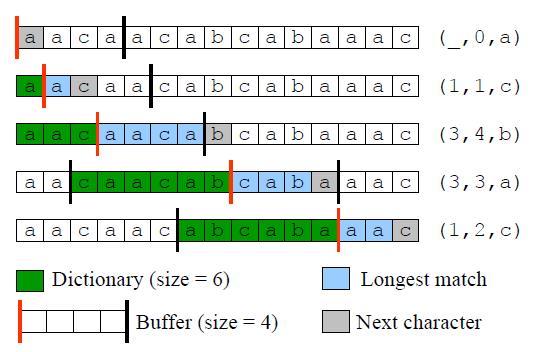
LZ77的变形
***LZR:***就是SB搜索缓冲的长度不固定了,算法输出的token位长度也是可变的。
***LZH:***算法的输出结果又进行了哈夫曼编压缩。
***DEFLATE:***当前最流行的基于LZ77的压缩算法,是很多通用的Unix压缩项目‘gzip’的一部分。
LZ78:
算法是将编码过程中之前编码过的所有字符作为了一个索引字典,之前的每一次编码是一个字典元素,之后的编码如果包含之前字典的元素则用该元素的索引代替实现压缩(注意是从之前的字典元素中找那个匹配最长的字典元素),同时记录不匹配的那个字符。可以想到,不断更新的字典中最长的字典元素很可能会越来越长且每次长一个字符。
***示例:***对字符串“abacbabaccbabbaca“进行LZ78编码。
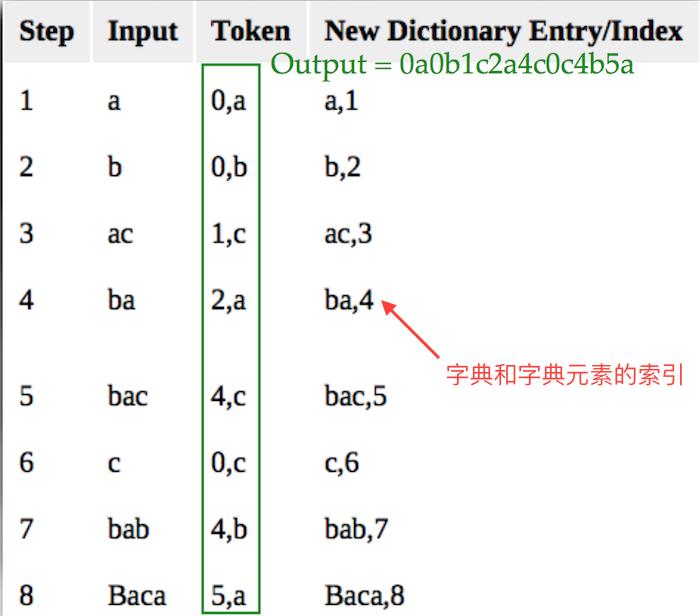
LZ78的变形算法
上面说到LZ78的最长的字典元素只会越来越长不受限制,那么就要使用变长的bit空间来保存字典索引,当前字典的需要保存索引的空间大小为$log2 (i)$ bits, $i$为目前字典中最长字典元素的长度。
LZC
算法给字典元素的长度设置一个最大值,如果匹配的结果超出最大值时就选择上一个相对较短的匹配的字典元素,防止字典元素变得太长。如果编码压缩率受限制变得太小,就清空之前的字典,比如重新开始压缩算法。
LZW
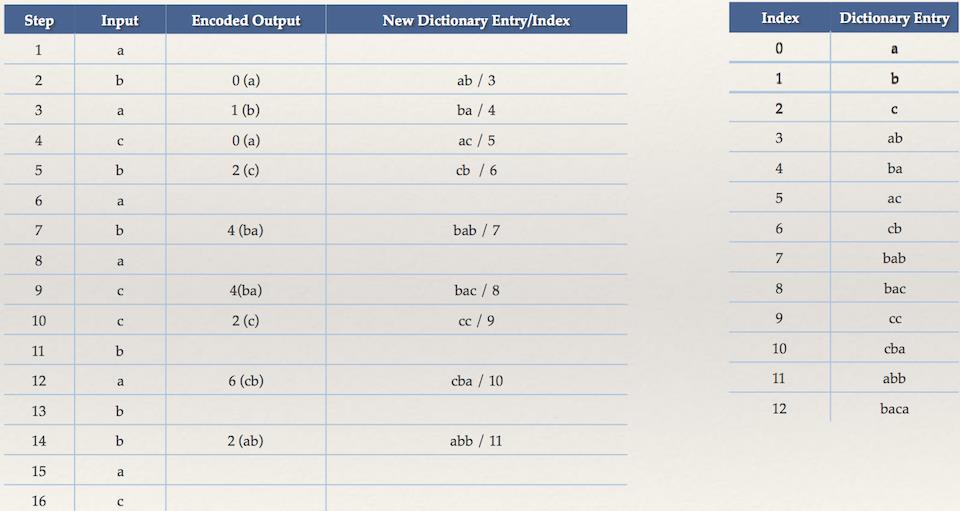
和LZ78不同的是,算法开始不是空的字典,一开始就把可能的所有单一字符作为最开始的字典,另外不是和LZ78那样记录字典索引和不匹配字符,而是只记录匹配的字典索引(不可能出现不匹配的情况,至少匹配一个字符了)。
***示例:***对字符串“abacbabaccbabbaca”进行LZW编码:
算术编码
算数编码是考虑到解决哈夫曼编码的一个限制:对于信息的编码,要对每一个字符都要使用一个几个二进制的bit数区别表示,收到整体的影响,平均每个字符可能都要用不少的bit数空间来表示。
算术编码是将编码的消息表示成实数0和1之间的一个间隔,消息越长,编码表示它的间隔就越小,形成结合越来越紧密的编码,同时需要表示的二进制位数就越多,导致算数编码的最大问题就是计算机的精度问题,精度有限,正常情况下无法进行大量数据的编码,事实上只能编码很短的数据。后来有了其他的先进方法才使算术编码得到应用,具体参考算数编码文章链接。
推荐阅读:算术编码
以上是关于无损压缩经典算法的主要内容,如果未能解决你的问题,请参考以下文章