稀疏矩阵的列序递增法和一次定位快速转置法

Posted 2022-07-28 岩枭

稀疏矩阵：矩阵中大多数元素为0的矩阵，从直观上讲，当非零元素个数低于总元素的30%时，这样的矩阵为稀疏矩阵。

如：

int array [6][5] =     1, 0, 3, 0, 5,                      

                        0, 0, 0, 0, 0,                      

                        0, 0, 0, 0, 0,                     

                        1, 0, 3, 0, 5,                     

                        0, 0, 0, 0, 0,                 

                        0, 0, 0, 0, 0;

稀疏矩阵的压缩存储：使用row,col,value三元组存储每一个有效数据，三元组按原矩阵中的位置，以行优先级先后顺序依次存放。

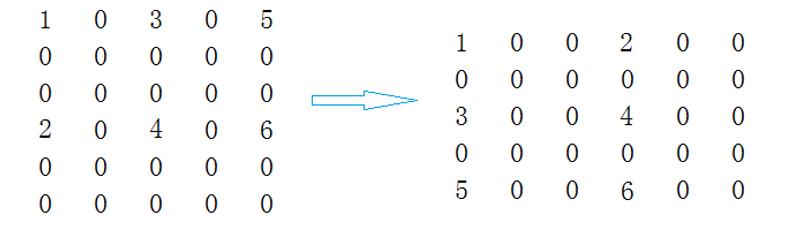
矩阵的转置：将原矩阵的行、列对换，也就是将[i][j]和[j][i]位置上的数据对换。

稀疏矩阵的列序递增法：

    按照被转置矩阵三元组表A的序列（即转置后三元组表B的行序）递增的顺序进行转置，则转置后矩阵的三元组表B恰好是以“行序为主序的”.

一次定位快速转置法：

    在列转置中算法的时间浪费主要在双重循环中，要改善算法的性能，必须去掉双重循环，使得整个转置过程通过一次循环来完成。

为了使得被转置的三元组表A中元素一次定位到三元组表B中，需要计算一下以下数据：

1）RowCounts,三元组表A中每一列有效值的个数，即转置后矩阵三元组表B中每一行有效值的个数。

2）RowStart,三元组表B中每一行有效值的起始位置。

RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];

代码实现：

#include <iostream>

using namespace std;

#include <vector>//动态数组

//三元组

template<class T>

struct Triple

size_t _row;

size_t _col;

T _value;

Triple(size_t row = 0, size_t col = 0, const T& value = T())

:_row(row)

, _col(col)

, _value(value)

;

template<class T>

class SparseMatrix

public://invalid   非零值

SparseMatrix(T* a = NULL, size_t M = 0, size_t N = 0, const T& invalid = T())

:_rowSize(M)

, _colSize(N)

, _invalid(invalid)

for (size_t i = 0; i < M; ++i)

for (size_t j = 0; j < N; ++j)

if (a[i*N + j] != _invalid)//每行元素个数就是列的个数

Triple<T> t;

t._row = i;

t._col = j;

t._value = a[i*N + j];

_a.push_back(t);//在Vector类，插入一个元素

void Display()

size_t index = 0;

for (size_t i = 0; i < _rowSize; ++i)

for (size_t j = 0; j < _colSize; ++j)

if (index < _a.size()&& (_a[index]._row == i)&& (_a[index]._col == j))

cout << _a[index++]._value << " ";

else

cout << _invalid << " ";

cout << endl;

//矩阵列序递增转置算法，时间复杂度为O(有效数据的个数*原矩阵的列数)

SparseMatrix<T> Transport()

SparseMatrix<T> sm;

sm._colSize = _rowSize;

sm._rowSize = _colSize;

sm._invalid = _invalid;

for (size_t i = 0; i < _colSize; ++i)//列序递增

size_t index = 0;

while (index < _a.size())

if (_a[index]._col == i)

Triple<T> t;

t._row = _a[index]._col;

t._col = _a[index]._row;

t._value = _a[index]._value;

sm._a.push_back(t);

++index;

return sm;

//一次定位计数快速转置 时间复杂度为O(有效数据的个数+原矩阵的列数)

SparseMatrix<T> FastTransport()

SparseMatrix<T> sm;

sm._rowSize = _colSize;

sm._colSize = _rowSize;

sm._invalid = _invalid;

int* RowCounts = new int[_colSize];//计数

int* RowStart = new int[_colSize];//位置

memset(RowCounts, 0, sizeof(int)*_colSize);

memset(RowStart, 0, sizeof(int)*_colSize);

size_t index = 0;//index  非零元素

while (index < _a.size())

++RowCounts[_a[index]._col];

++index;

for (size_t i = 1; i < _colSize; ++i)

RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];

index = 0;

sm._a.resize(_a.size());

while (index < sm._a.size())

Triple<T> t;

t._row = _a[index]._col;

t._col = _a[index]._row;

t._value = _a[index]._value;

sm._a[RowStart[_a[index]._col]] = t;

++RowStart[_a[index]._col];

++index;

delete[] RowCounts;

delete[] RowStart;

return sm;

protected:

vector<Triple<T>> _a;

size_t _rowSize;

size_t _colSize;

T _invalid;

;

void Test()

int array[5][4] =

1, 0, 3, 0 ,

0, 0, 0, 0 ,

0, 0, 0, 0 ,

2, 0, 4, 5 ,

0, 0, 0, 0 ,

;

SparseMatrix<int> sm1((int*)array, 5, 4, 0);

cout << "打印原矩阵："<<endl;

sm1.Display();

cout << endl;

cout << "打印转置后的矩阵：" << endl;

SparseMatrix<int> sm2 = sm1.Transport();

/*SparseMatrix<int> sm2 = sm1.FastTransport();*/

sm2.Display();

int main()

Test();

system("pause");

return 0;

运行结果：

打印原矩阵：

1 0 3 0

0 0 0 0

0 0 0 0

2 0 4 5

0 0 0 0

打印转置后的矩阵：

1 0 0 2 0

0 0 0 0 0

3 0 0 4 0

0 0 0 5 0

请按任意键继续. . .

两种算法比较：

    假设有效数据的个数为100，原矩阵的列数为100，矩阵列序递增转置算法，时间耗费为O(有效数据的个数*原矩阵的列数)，即100*100=10000次；一次定位计数快速转置算法，时间复杂度为O(有效数据的个数+原矩阵的列数)，即100+100=200次左右。显然一次定位计数快速转置算法的时间效率要高的多，在时间性能上优于列序递增转置法，但是在空间耗费上增加了两个辅助向量空间,即RowCounts和RowStart,由此可见，算法在时间上的节省是以更多的存储空间为代价的。

本文出自 “岩枭” 博客，请务必保留此出处http://yaoyaolx.blog.51cto.com/10732111/1775877