每日一题729. 我的日程安排表 I

Posted 2022-07-09 王六六的IT日常

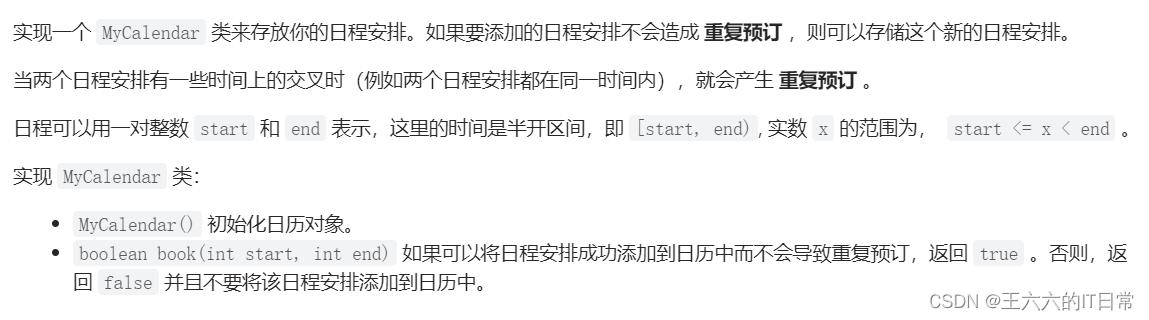
729. 我的日程安排表 I


参考：大佬在力扣题解写的博文-----线段树详解「汇总级别整理 🔥🔥🔥」
线段树系列：
线段树解决的是「区间和」的问题，且该「区间」会被修改。
举个简单的🌰，对于 nums = [1, 2, 3, 4, 5]。
如果我们需要多次求某一个区间的和，是不是首先想到了利用「前缀和」。
关于前缀和的详细介绍可见👉 前缀和数组

nums = [1, 2, 3, 4, 5] 对应的线段树如下所示：

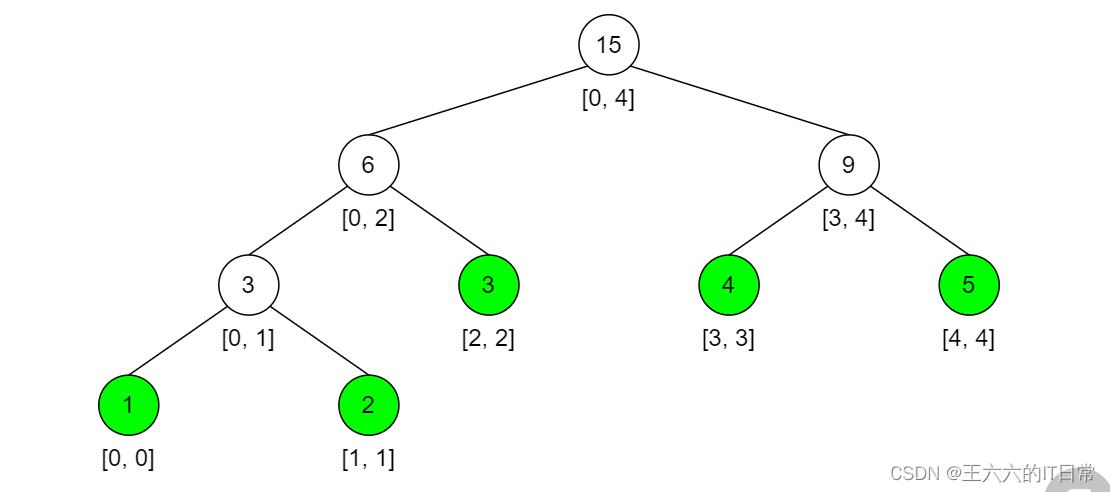
每个节点代表一个区间，而节点的值就是该区间的和。

• 数字之和「总数字之和 = 左区间数字之和 + 右区间数字之和」
• 最大公因数 (GCD)「总 GCD = gcd(左区间 GCD, 右区间 GCD)」
• 最大值「总最大值 = max(左区间最大值，右区间最大值)」

线段树的数据结构
我们可以使用数组来表示一棵线段树，假如根节点为 i，那么左孩子的节点就为 2 * i，右孩子的节点就为 2 * i + 1 (前提：i 从 1 开始)

我们可以使用链表来表示一棵线段树，其节点的数据结构如下：

class Node 
    // 左右孩子节点
    Node left, right;
    // 当前节点值
    int val;

比较倾向使用链表，因为比较节约内存，下面的实现均基于链表。

线段树的建立

如果题目中给了具体的区间范围，我们根据该范围建立线段树。

public void buildTree(Node node, int start, int end) 
    // 到达叶子节点
    if (start == end) 
        node.val = arr[start];
        return ;
    
    int mid = (start + end) >> 1;
    buildTree(node.left, start, mid);
    buildTree(node.right, mid + 1, end);
    // 向上更新
    pushUp(node);

// 向上更新
private void pushUp(Node node) 
    node.val = node.left.val + node.right.val;

但是很多时候，题目中都没有给出很具体的范围，只有数据的取值范围，一般都很大，所以我们更常用的是「动态开点」。
「动态开点」一般是在「更新」或「查询」的时候动态的建立节点，具体可见下面的更新和查询操作。

线段树完整模版

注意：下面模版基于求「区间和」以及对区间进行「加减」的更新操作，且为「动态开点」

/**
 * @Description: 线段树（动态开点）
 * @Author: LFool
 * @Date 2022/6/7 09:15
 **/
public class SegmentTreeDynamic 
    class Node 
        Node left, right;
        int val, add;
    
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) 
        if (l <= start && end <= r) 
            node.val += (end - start + 1) * val;
            node.add += val;
            return ;
        
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    
    public int query(Node node, int start, int end, int l, int r) 
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    
    private void pushUp(Node node) 
        node.val = node.left.val + node.right.val;
    
    private void pushDown(Node node, int leftNum, int rightNum) 
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add * leftNum;
        node.right.val += node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    

class MyCalendar 

    public MyCalendar() 

    
    
    public boolean book(int start, int end) 
        // 先查询该区间是否为 0
        if (query(root, 0, N, start, end - 1) != 0) return false;
        // 更新该区间
        update(root, 0, N, start, end - 1, 1);
        return true;
    
    // *************** 下面是模版 ***************
    class Node 
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) 
        if (l <= start && end <= r) 
            node.val += val;
            node.add += val;
            return ;
        
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    
    public int query(Node node, int start, int end, int l, int r) 
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    
    private void pushUp(Node node) 
        // 每个节点存的是当前区间的最大值
        node.val = Math.max(node.left.val, node.right.val);
    
    private void pushDown(Node node) 
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add;
        node.right.val += node.add;
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    



/**
 * Your MyCalendar object will be instantiated and called as such:
 * MyCalendar obj = new MyCalendar();
 * boolean param_1 = obj.book(start,end);
 */