第一节2:DBSCAN算法Python实现和效果展示
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第一节2:DBSCAN算法Python实现和效果展示相关的知识,希望对你有一定的参考价值。
文章目录
五:Python实现
代码如下
import random
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def dbscan(data_set, eps, min_pts):
examples_nus = np.shape(data_set)[0] # 样本数量
unvisited = [i for i in range(examples_nus)] # 未被访问的点
visited = [] # 已被访问的点
# cluster为输出结果,表示对应元素所属类别
# 默认是一个长度为examples_nus的值全为-1的列表,-1表示噪声点
cluster = [-1 for i in range(examples_nus)]
k = - 1 # 用k标记簇号,如果是-1表示是噪声点
while len(unvisited) > 0: # 只要还有没有被访问的点就继续循环
p = random.choice(unvisited) # 随机选择一个未被访问对象
unvisited.remove(p)
visited.append(p)
p_nighbor = [] # nighbor为p的eps邻域对象集合,密度直接可达
for i in range(examples_nus):
if i != p and np.sqrt(np.sum(np.power(data_set[i, :]-data_set[p, :], 2))) <= eps: # 计算距离,看是否在邻域内
p_nighbor.append(i)
if len(p_nighbor) >= min_pts: # 如果邻域内对象个数大于min_pts说明是一个核心对象
k = k+1
cluster[p] = k # 表示p它属于k这个簇
for q in p_nighbor: # 现在要找该邻域内密度可达
if q in unvisited:
unvisited.remove(q)
visited.append(q)
# nighbor_pi是pi的eps邻域对象集合
q_nighbor = []
for j in range(examples_nus):
if np.sqrt(np.sum(np.power(data_set[j]-data_set[q], 2))) <= eps and j != q:
q_nighbor.append(j)
if len(q_nighbor) >= min_pts: # pi是否是核心对象,通过他的密度直接可达产生p的密度可达
cluster[q] = k
for t in q_nighbor:
if t not in p_nighbor:
p_nighbor.append(t)
else:
cluster[p] = -1 # 不然就是一个噪声点
return cluster
六:效果展示
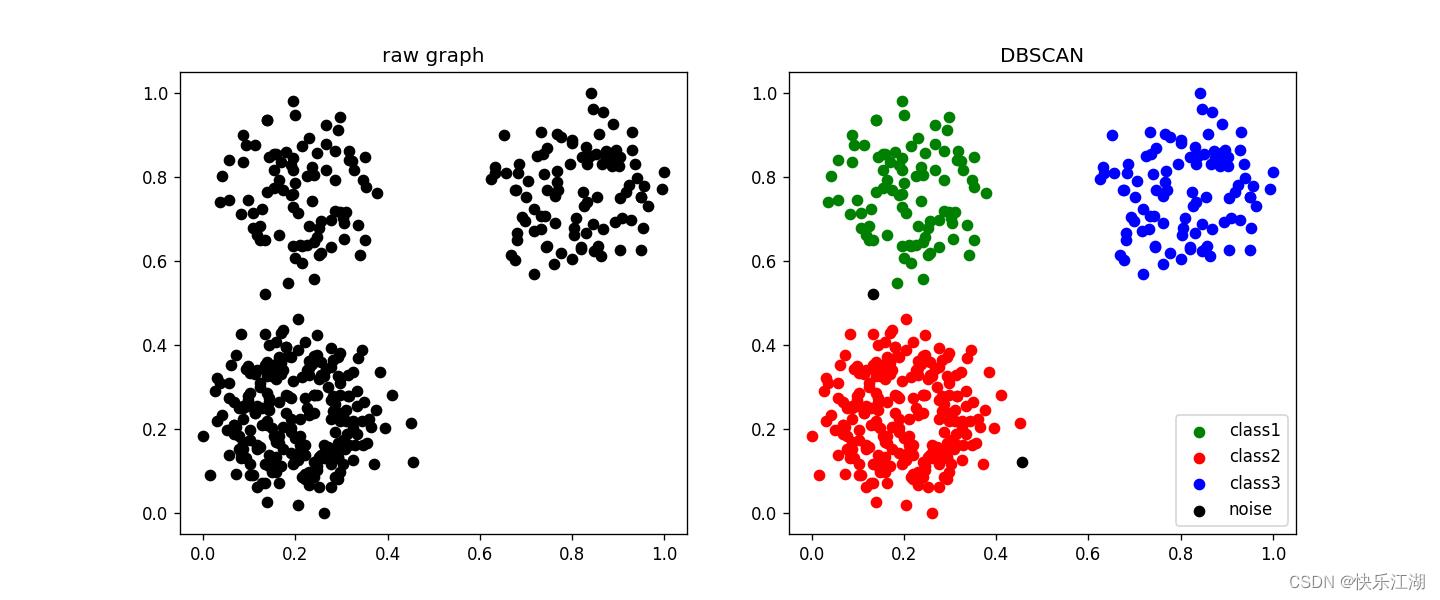
(1)人造数据集
eps=0.08min_pts=2
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import DBSCAN
raw_data = pd.read_csv('./dataset/438-3.csv', header=None)
raw_data.columns = ['X', 'Y']
x_axis = 'X'
y_axis = 'Y'
examples_num = raw_data.shape[0]
train_data = raw_data[[x_axis, y_axis]].values.reshape(examples_num, 2)
min_vals = train_data.min(0)
max_vals = train_data.max(0)
ranges = max_vals - min_vals
normal_data = np.zeros(np.shape(train_data))
nums = train_data.shape[0]
normal_data = train_data - np.tile(min_vals, (nums, 1))
normal_data = normal_data / np.tile(ranges, (nums, 1))
# 参数
eps = 0.08
min_pts = 2
cluster = DBSCAN.dbscan(normal_data, eps, min_pts)
plt.figure(figsize=(12, 5), dpi=80)
# 第一幅图已知标签
plt.subplot(1, 2, 1)
plt.scatter(normal_data[:, 0], normal_data[:, 1], color='black')
plt.title('raw graph')
# 第二幅图聚类结果
plt.subplot(1, 2, 2)
class1_X = []
class1_Y = []
class2_X = []
class2_Y = []
class3_X = []
class3_Y = []
noise_X = [] # 噪声点
noise_Y = [] # 噪声点
for index, value in enumerate(cluster):
if value == 0:
class1_X.append(normal_data[index][0])
class1_Y.append(normal_data[index][1])
elif value == 1:
class2_X.append(normal_data[index][0])
class2_Y.append(normal_data[index][1])
elif value == 2:
class3_X.append(normal_data[index][0])
class3_Y.append(normal_data[index][1])
elif value == -1:
noise_X.append(normal_data[index][0])
noise_Y.append(normal_data[index][1])
plt.scatter(class1_X, class1_Y, c='g', label='class1')
plt.scatter(class2_X, class2_Y, c='r', label='class2')
plt.scatter(class3_X, class3_Y, c='blue', label='class3')
plt.scatter(noise_X, noise_Y, c='black', label='noise')
plt.title('DBSCAN')
plt.legend()
plt.show()
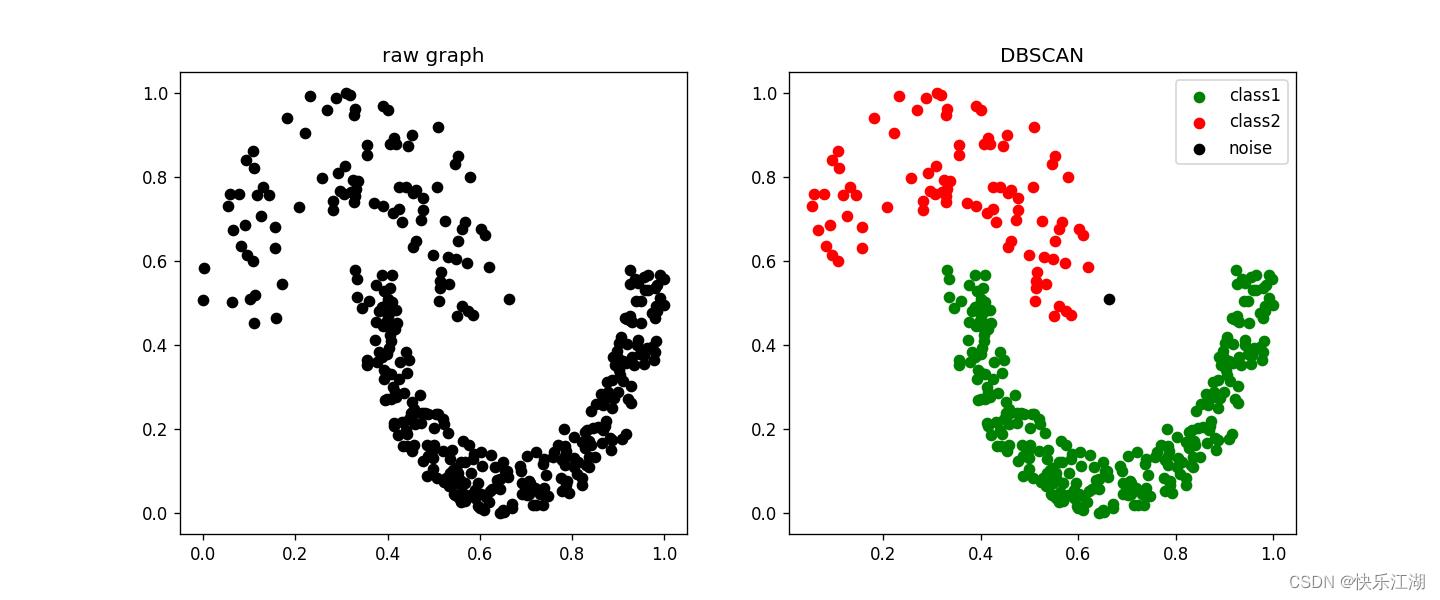
(2)Jain数据集
eps= 0.08min_pts= 1
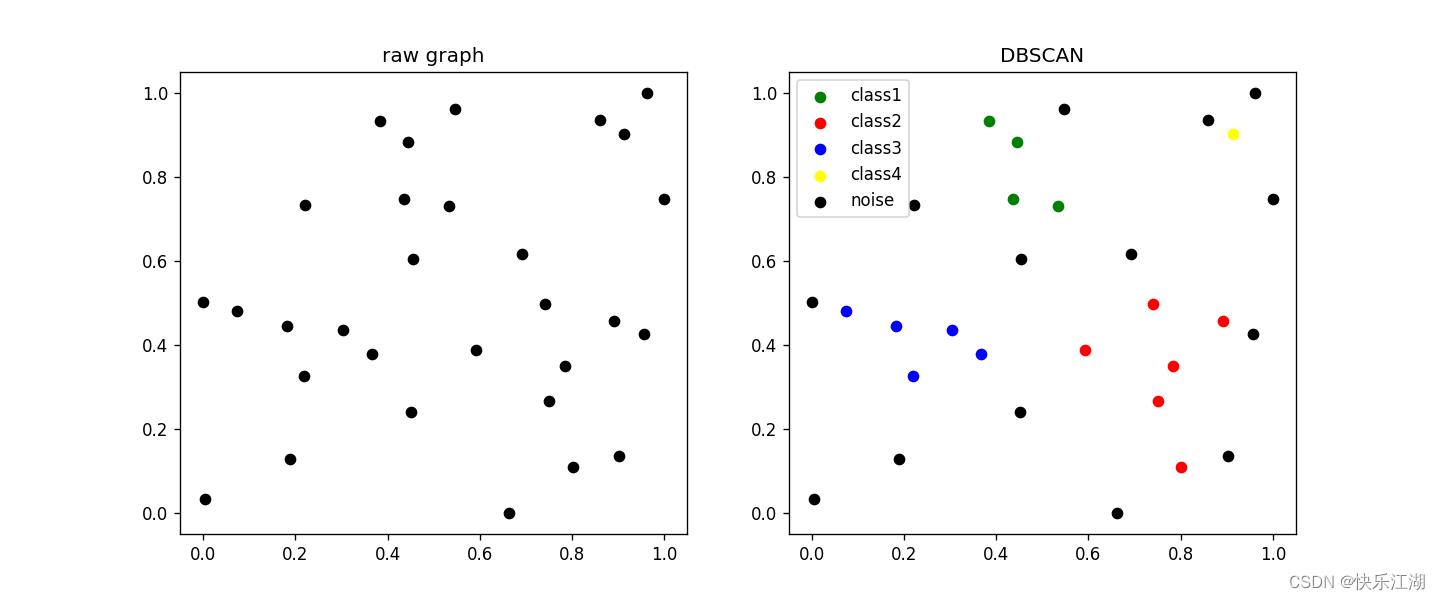
(3)melon数据集
eps= 0.22min_pts= 3
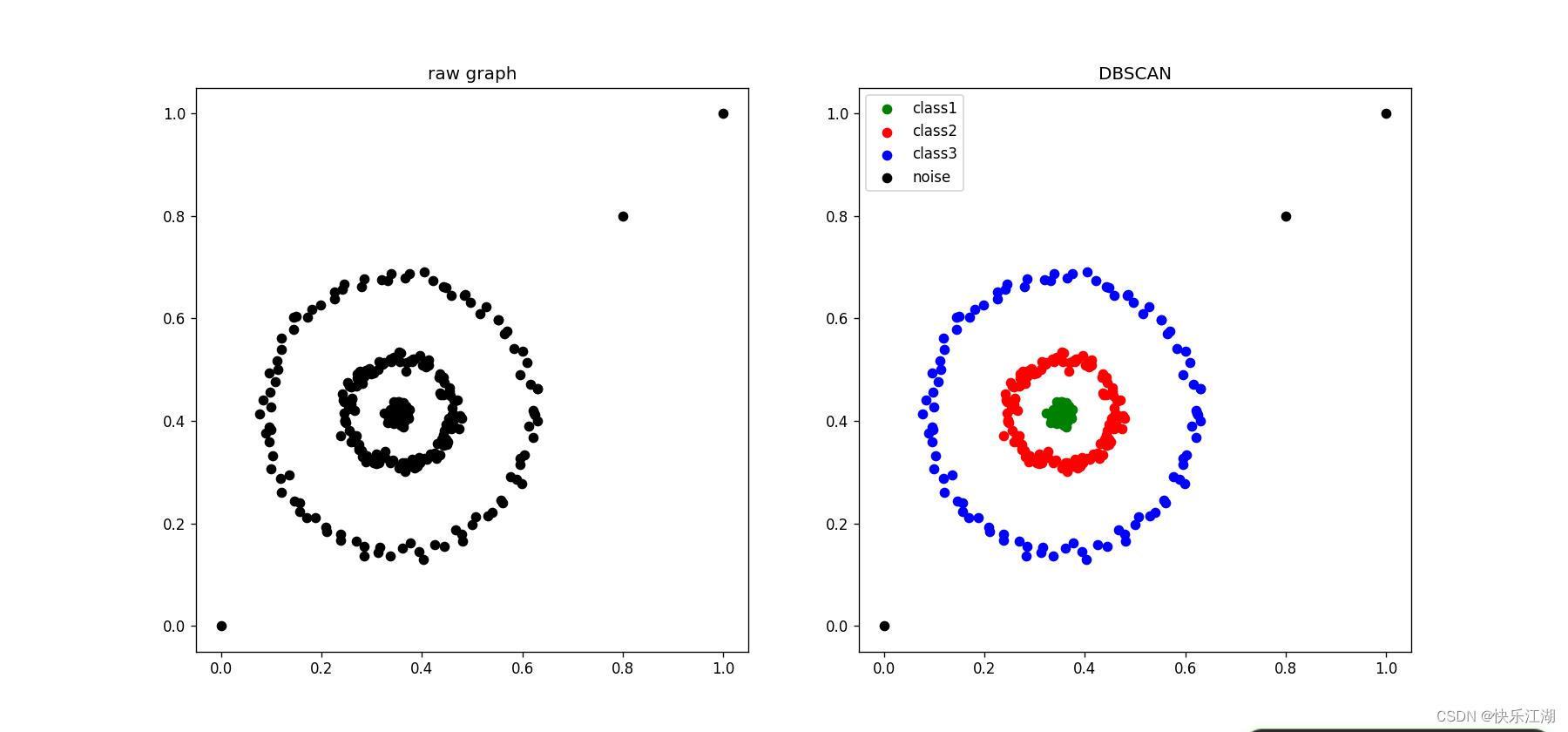
(4)threeCircles数据集
eps= 0.07min_pts= 4
(5)Spril数据集
eps= 0.08min_pts= 2
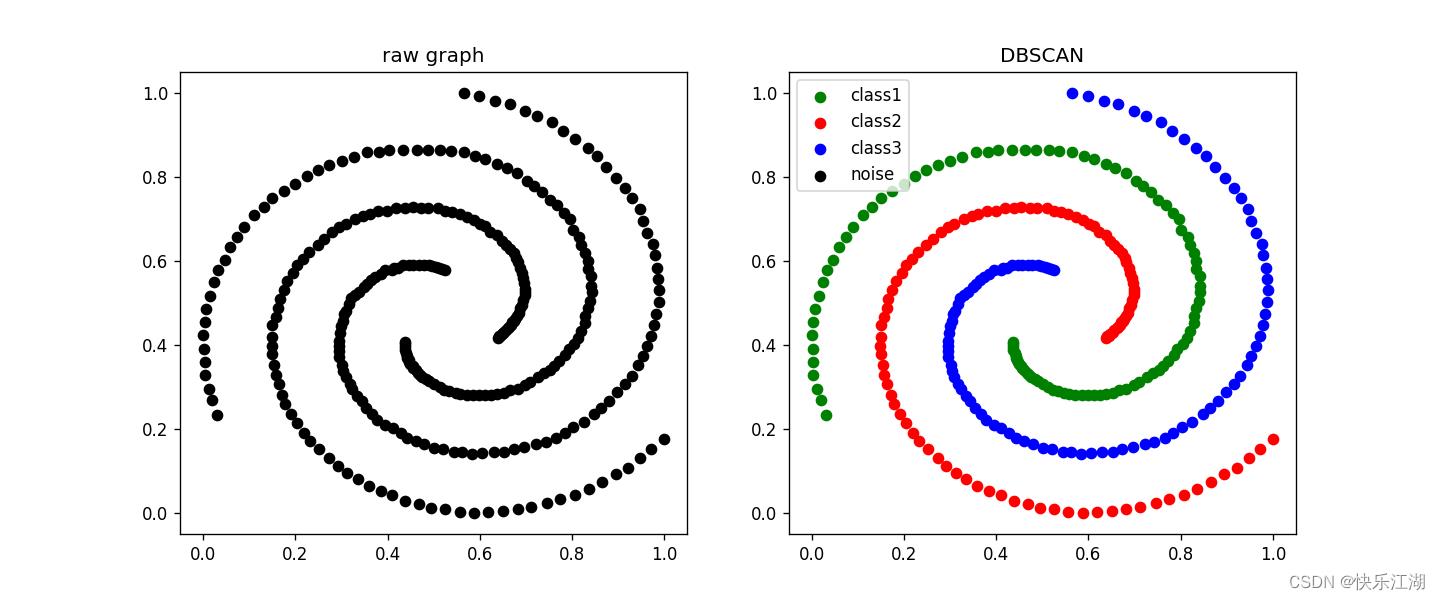
(6)Square数据集
eps= 0.04min_pts= 3
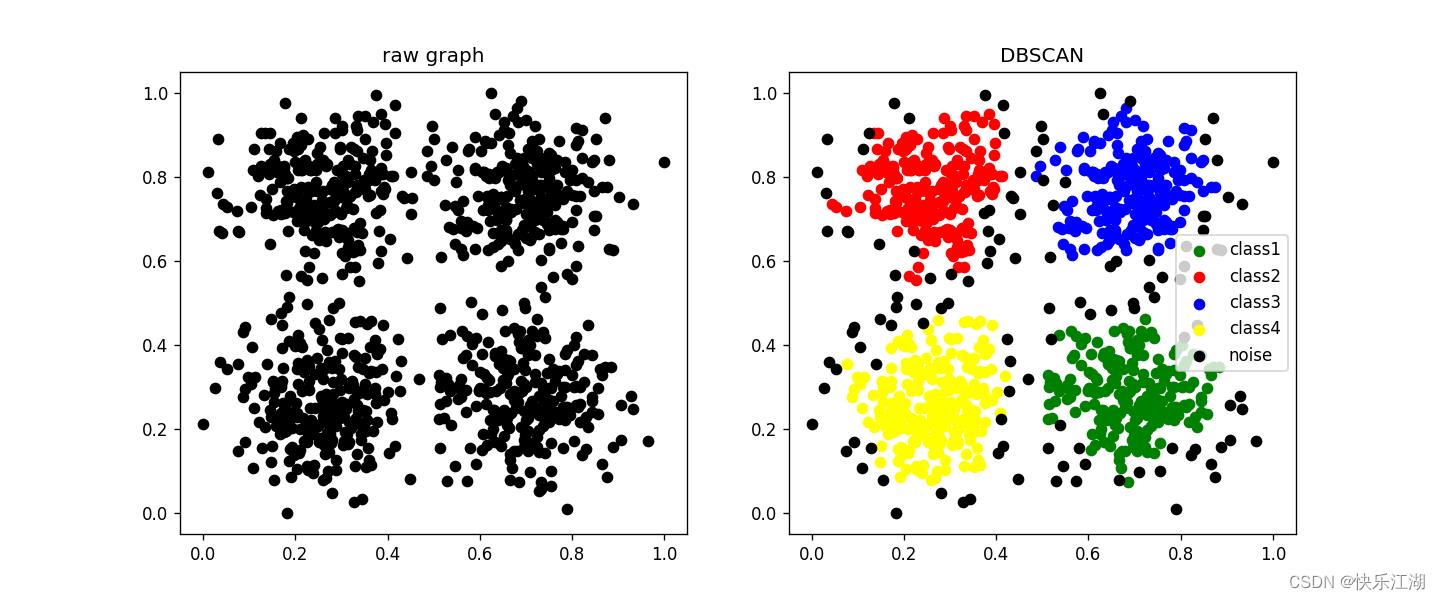
(7)lineblobs数据集
eps= 0.12min_pts= 4
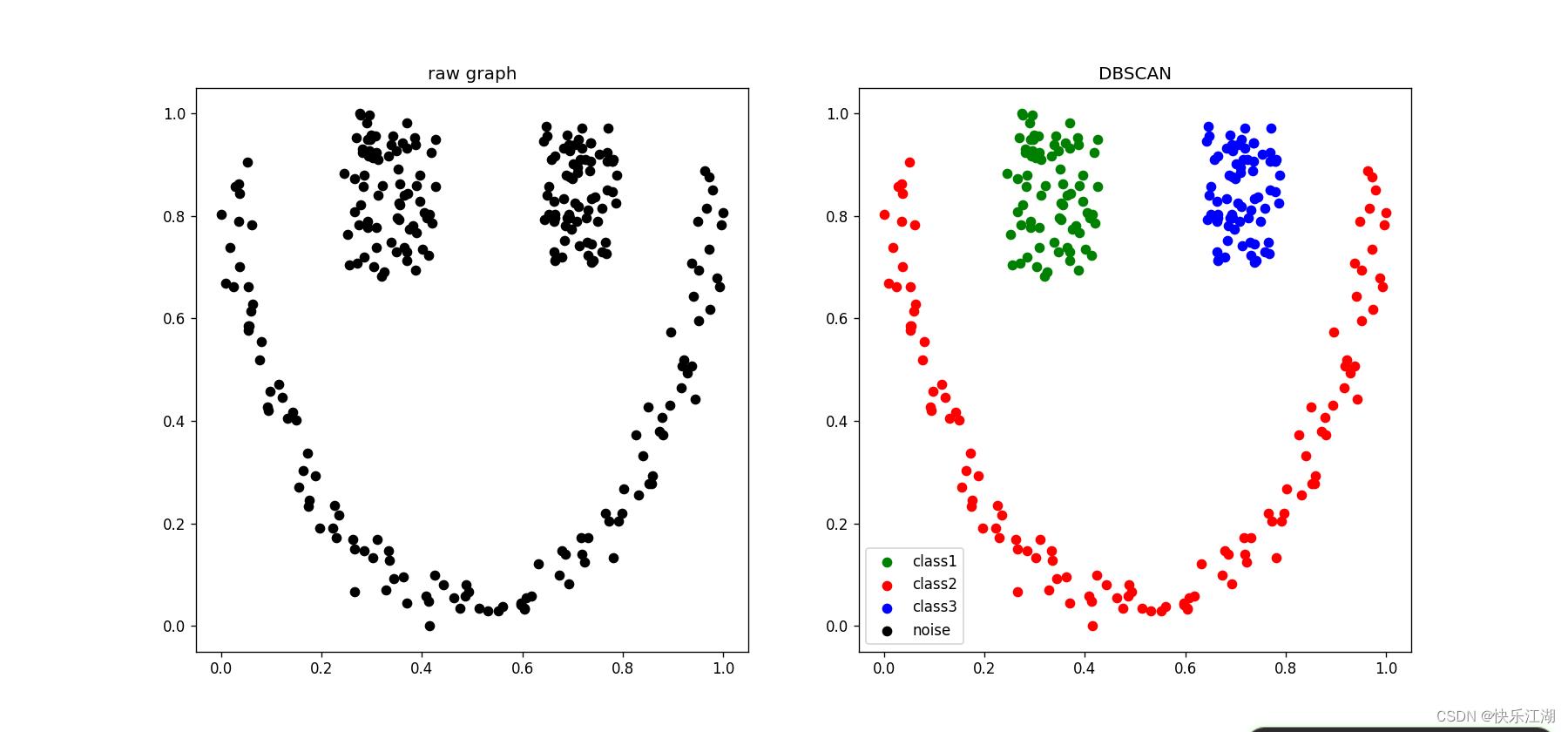
(8)788points数据集
eps= 0.04min_pts= 3
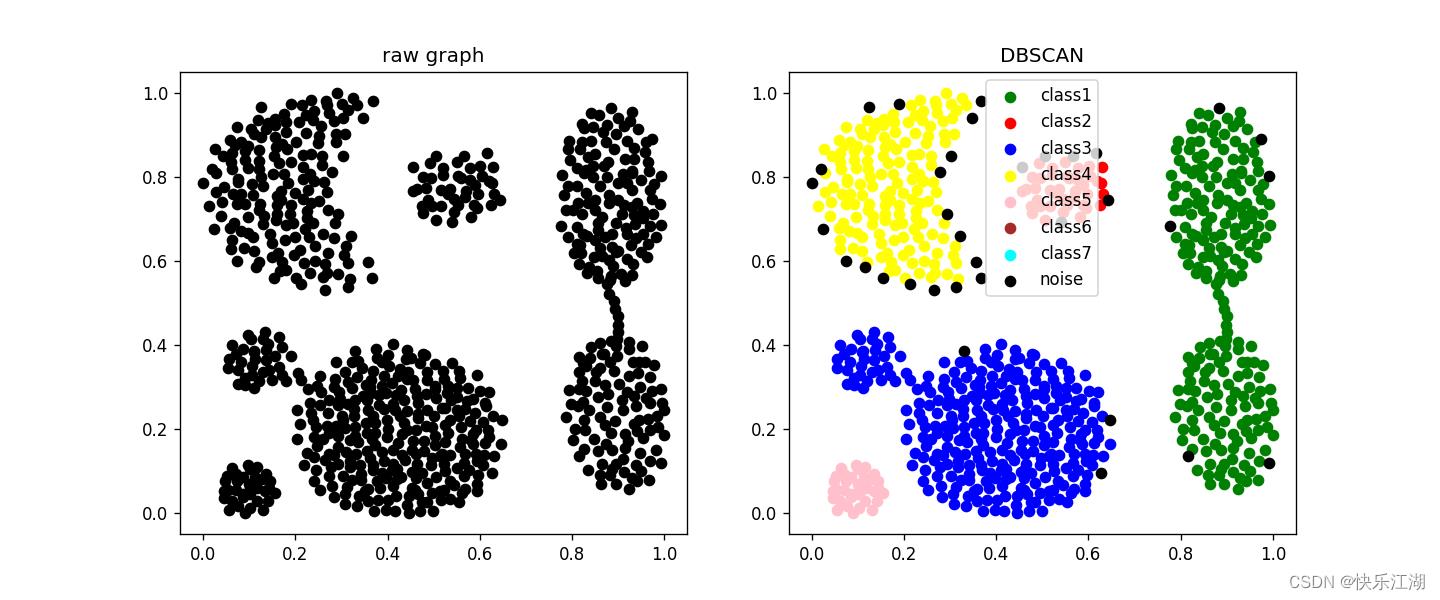
(9)gassian数据集
eps= 0.05min_pts= 4
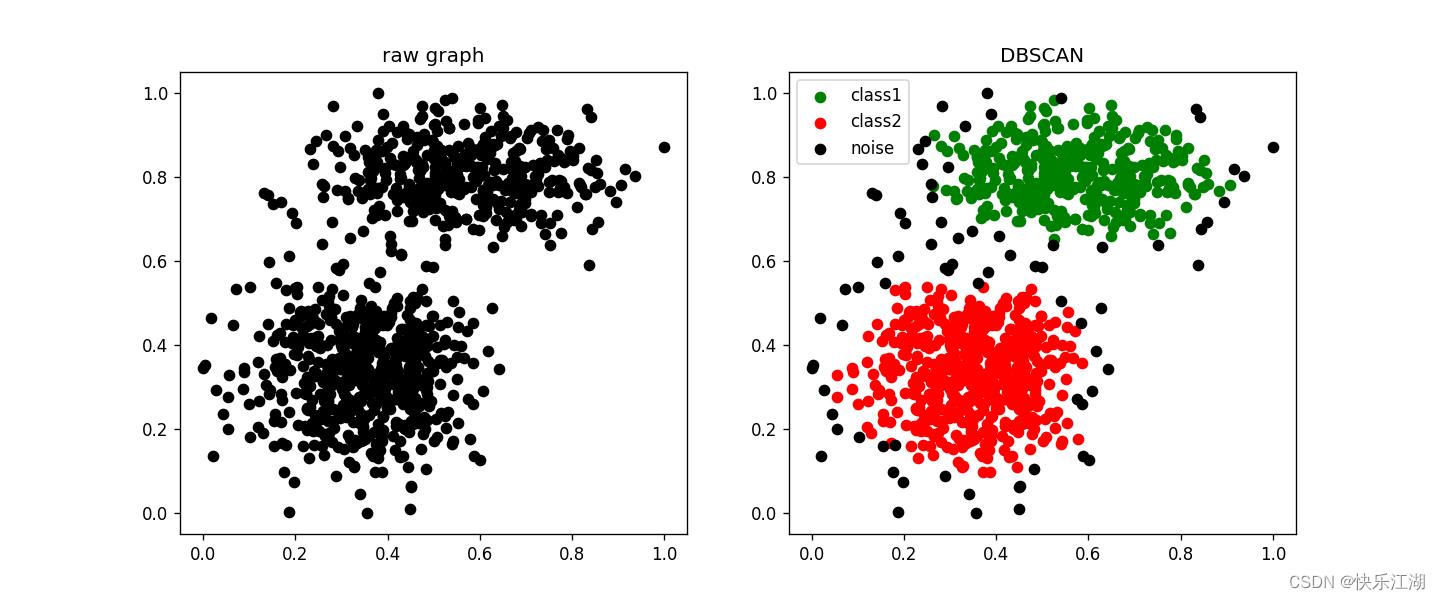
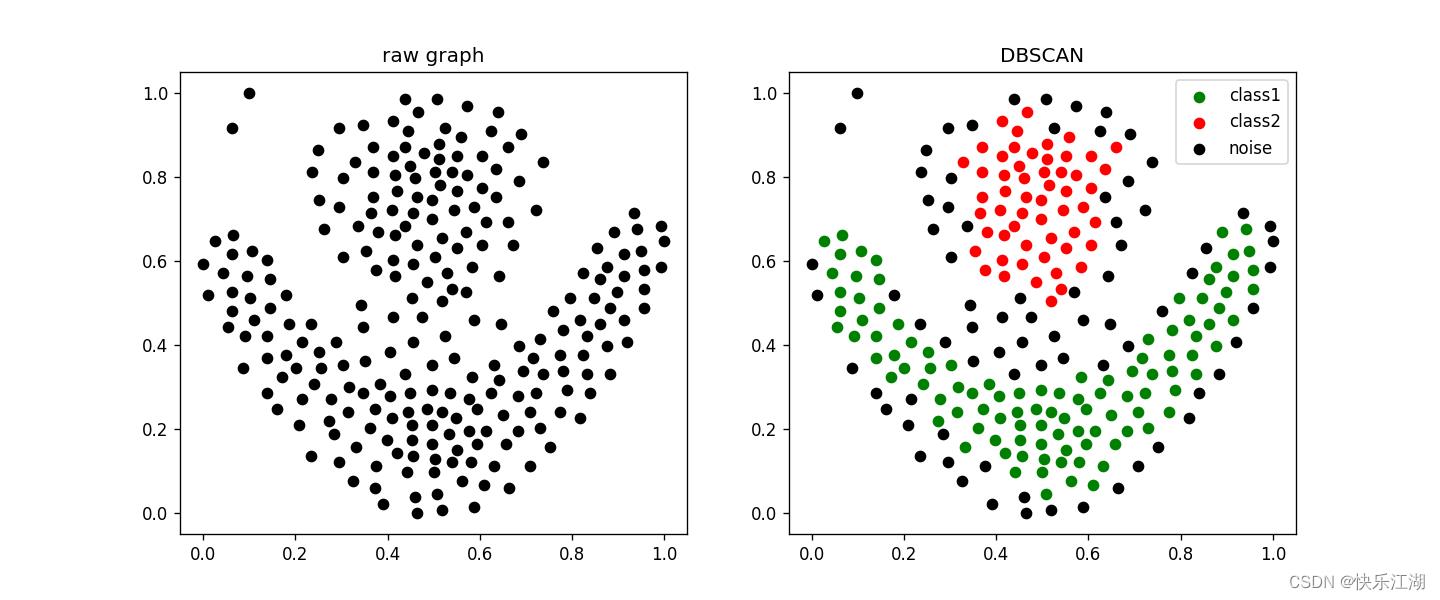
(10)arrevation数据集
eps= 0.06min_pts= 3
以上是关于第一节2:DBSCAN算法Python实现和效果展示的主要内容,如果未能解决你的问题,请参考以下文章