每日一题241. 为运算表达式设计优先级

Posted 2022-07-04 王六六的IT日常

241. 为运算表达式设计优先级

参考题解：https://leetcode.cn/problems/different-ways-to-add-parentheses/solution/wei-yun-suan-biao-da-shi-she-by-jiang-hu-0pf0/

• 递归
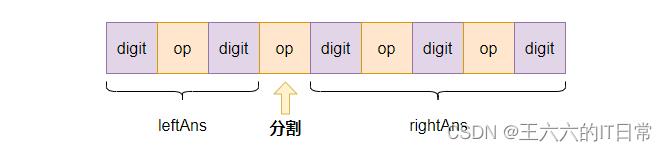
  把字符串按照操作符分割为两个子表达式，将两个子表达式的结果集进行当前op的操作，组装成新的结果集，对每个op分别进行分割得到的结果集之和就是最终的答案。而子表达式又是相同的问题，可以采用递归进行计算，最终会递归到一个digit上。
  

class Solution 
    public List<Integer> diffWaysToCompute(String expression) 
        //表达式为空
        if (expression == null || expression.length() == 0) 
            return new ArrayList<>();
        
        char[] chars = expression.toCharArray();
        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < chars.length; i++) 
            char aChar = chars[i];
            //如果当前字符是操作符，也就是op，进行分割
            if (!Character.isDigit(aChar)) 
                //递归拿到左右两个表达式的结果集
                List<Integer> leftList = diffWaysToCompute(expression.substring(0, i));
                List<Integer> rightList = diffWaysToCompute(expression.substring(i + 1));
                //对两个结果集的所有结果进行op运算
                for (Integer left : leftList) 
                    for (Integer right : rightList) 
                        if (aChar == '+') 
                            ans.add(left + right);
                         else if (aChar == '-') 
                            ans.add(left - right);
                         else 
                            ans.add(left * right);
                        
                    
                
            
        
        //结果集是空，证明该字符串是数字，将数字加入结果集
        if (ans.isEmpty()) 
            ans.add(Integer.valueOf(expression));
        
        return ans;
    

• 动态规划
  因为最终的答案是由一个个子问题（子表达式）的答案所构成，所以可以采用动态规划，将问题划分为一个个子问题来求解。
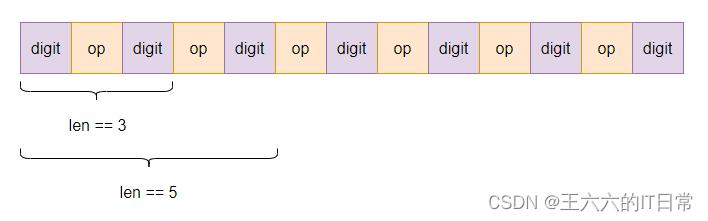
  首先我们将字符串分成digit、op、digit、op、digit、op、digit…这样的序列,并且可知序列的长度是奇数个,所以子问题的最小长度为3（长度为1的digit不需要计算）,也就是一个op运算需要至少三个元素（两个digit和一个op），下一个子问题的长度为当前子问题+2（加一个op和一个digit）,所以我们可以从最小长度为3的子问题一步步求解最大长度的解。
  

class Solution 
    public List<Integer> diffWaysToCompute(String expression) 
        List<Object> ops = new ArrayList<>();
        //将字符串分割为digit、op、digit、op、digit......这样的序列
        for (int i = 0; i < expression.length(); ) 
            if (!Character.isDigit(expression.charAt(i))) 
                //添加操作符
                ops.add(expression.charAt(i));
                i++;
             else 
                //添加数字
                int digit = 0;
                while (i < expression.length() && Character.isDigit(expression.charAt(i))) 
                    digit = digit * 10 + expression.charAt(i) - '0';
                    i++;
                
                ops.add(digit);
            
        
        //dp[i][j]表示从i到j子问题（子表达式）的所有答案
        List<Integer>[][] dp = new List[ops.size()][ops.size()];
        for (int i = 0; i < ops.size(); i++) 
            for (int j = 0; j < ops.size(); j++) 
                dp[i][j] = new ArrayList<>();
            
        
        //初始时，所有的digit都是自己本身并且数字都是隔着存放的，并且位置固定在偶数位(0,2,4...) 所以+2
        //eg：digit、op、digit、op、digit......
        for (int i = 0; i < ops.size(); i += 2) 
            dp[i][i].add((int) ops.get(i));
        
        //从长度为3的子问题开始计算
        for (int len = 3; len <= ops.size(); len += 2) 
            //左边界从0开始
            for (int left = 0; left + len <= ops.size(); left += 2) 
                //右边界
                int right = left + len - 1;
                //按照op进行分割左右两个子表达式 +2表示下一个op
                for (int k = left + 1; k < right; k += 2) 
                    List<Integer> leftAns = dp[left][k - 1];
                    List<Integer> rightAns = dp[k + 1][right];
                    //对左右两个子表达式的结果集进行合并处理
                    for (int num1 : leftAns) 
                        for (int num2 : rightAns) 
                            char op = (char) ops.get(k);
                            if (op == '+') 
                                dp[left][right].add(num1 + num2);
                             else if (op == '-') 
                                dp[left][right].add(num1 - num2);
                             else if (op == '*') 
                                dp[left][right].add(num1 * num2);
                            
                        
                    
                
            
        
        return dp[0][ops.size() - 1];
    

• DFS
  参考：https://leetcode.cn/problems/different-ways-to-add-parentheses/solution/by-ac_oier-z07i/

class Solution 
    char[] cs;
    public List<Integer> diffWaysToCompute(String s) 
        cs = s.toCharArray();
        return dfs(0, cs.length - 1);
    
    List<Integer> dfs(int l, int r) 
        List<Integer> ans = new ArrayList<>();
        for (int i = l; i <= r; i++) 
            if (cs[i] >= '0' && cs[i] <= '9') continue;
            List<Integer> l1 = dfs(l, i - 1), l2 = dfs(i + 1, r);
            for (int a : l1) 
                for (int b : l2) 
                    int cur = 0;
                    if (cs[i] == '+') cur = a + b;
                    else if (cs[i] == '-') cur = a - b;
                    else cur = a * b;
                    ans.add(cur);
                
            
        
        if (ans.isEmpty()) 
            int cur = 0;
            for (int i = l; i <= r; i++) cur = cur * 10 + (cs[i] - '0');
            ans.add(cur);
        
        return ans;