2022深圳杯数学建模赛题思路 比赛通知

Posted 2022-06-27 dc_sinor

文章目录

• 0 前言
• 1 赛前准备 - 建模步骤
• • 1.1 第一步 提出问题
  • 1.2 第二步 选择建模方法
  • 1.3 第三步 推导模型的公式
  • 1.4 第四步 求解模型
  • 1.5 第五步 论文撰写
• 2 往届赛题思路 - 2021年羊狼追逐
• • 2.1 思路流程
  • 2.2 关键代码
  • 2.3 题解结果

---

0 前言

2022 年深圳杯竞赛时间官方目前还未放出消息，根据往年一般在2022年7月15月 — 9月10日之间，各位同学做好准备哦！

这里先占个坑，赛题出来后第一时间在这发布赛题思路

1 赛前准备 - 建模步骤

建模资料，获奖秘籍： https://gitee.com/math-sinor/math-data/blob/master/README.md

1.1 第一步 提出问题

• 整理出问题中涉及到的常量、变量与单位。
• 团队讨论出对变量所做的全部假设，包括等式和不等式。
• 用准确的数学表达式给出问题的目标。

1.2 第二步 选择建模方法

• 选择一个解决问题的一般求解方法。

1.3 第三步 推导模型的公式

• 将第1步中得到的问题整理成第2步选择的建模方法所需要形式。
• 注意统一前后字符、公式。

1.4 第四步 求解模型

• 将第2步中所选方法应用于第3步中推导的表达式中。
• 采用适当的软件对问题进行求解计算，常见软件如下。
  统计模型：EXCEL、SPSS、Eviews、Stata ，新手可直接上EXCEL。
  微分方程：Maple、Mathematic、Matlab
  文本排版：Word、Latex
  运筹规划：Matlab，Lingo
  公式整理：Mathtype
  智能算法：Matlab，R
  图像处理：Matlab，C++，OpenCV
  综上：Matlab万能，所以新手学会Matlab就足以应付竞赛。

1.5 第五步 论文撰写

• 用非技术性的语言将所做成果整理到文本上。
• 注意检查格式以及数学符号、术语。

2 往届赛题思路 - 2021年羊狼追逐

这里学长分享一个去年拿了国一的赛题思路，2022年的赛题思路将在赛题发布会5小时内发布~

2.1 思路流程

2.2 关键代码

'''
自己设置的环境类
智能体：羊
环境：羊、犬和圆形草地，犬采用最优围堵策略围堵羊，若羊在一段时间内逃出圈则胜利，这段时间内没逃出或者被犬抓到则失败；
状态空间：整个圆组成的点集，是二维的；
动作空间：羊每一步可采取的动作的集合
回报的设计：参照pendulum-v0游戏环境源码中的回报的设计方案。
'''
import gym
from gym import spaces
import numpy as np
import math
import random
from gym.envs.classic_control import rendering

sigma=10

# 将弧度转换为角度
def trans(tmp):
    return 360*(tmp/(2*np.pi))

# 更新犬的状态
def change_dog_state(thetaP,thetaE,delta_theta):
    new_thetaP=thetaP
    clockwise = (thetaP - delta_theta + 2 * np.pi) % (2 * np.pi)  # 顺时针
    counterclockwise = (thetaP + delta_theta + 2 * np.pi) % (2 * np.pi)  # 逆时针
    if thetaE > thetaP:
        if thetaE - thetaP >= np.pi:
            new_thetaP = clockwise
        else:
            new_thetaP = counterclockwise
    elif thetaE < thetaP:
        if thetaP - thetaE >= np.pi:
            new_thetaP = counterclockwise
        else:
            new_thetaP = clockwise
    return new_thetaP

# 计算夹角
def cal_angel(theta1,theta2):
    ans=0
    if theta1 > theta2:
        ans = theta1 - theta2
        if ans > np.pi:
            ans = 2 * np.pi - ans  # （补）角
    else:
        ans = theta2 - theta1
        if ans > np.pi:
            ans = 2 * np.pi - ans
    return ans

# 判断羊是否给抓住
def catch(R,theta1,theta2,theta3):
    x=R*np.cos(theta1)
    y=R*np.sin(theta1)
    a=R*np.cos(theta2)
    b=R*np.sin(theta2)
    A=R*np.cos(theta3)
    B=R*np.sin(theta3)
    len1=math.sqrt((x-a)*(x-a)+(y-b)*(y-b))
    len2=math.sqrt((x-A)*(x-A)+(y-B)*(y-B))
    if len1 <= sigma and len2 <= sigma:
        return True
    else:
        return False

class dogSheepEnv(gym.Env):
    def __init__(self):
        # self.dt = 0.2  # 采样时间
        self.dt=0.2
        # self.thetaP=np.pi/2# 狗的极坐标
        self.thetaP = random.uniform(0, 2 * np.pi)# 狗1的极坐标
        self.wP=np.pi/5# 狗的角速度
        self.thetaP2=random.uniform(0, 2 * np.pi)# 狗1的极坐标
        self.vE=32# 羊的速度
        self.thetaE=np.pi/2# 羊的极坐标
        self.radiusE=0# 羊的极坐标半径
        self.R=100# 圆的半径
        self.state=np.array([self.thetaE,self.radiusE,self.thetaP,self.thetaP2])# 环境的初始状态
        self.viewer = rendering.Viewer(400, 400)# 画板
        self.lambda1=0.07# reward的参数1
        self.lambda2=3.1# reward的参数2
        self.lambda3=3.1
        self.lambda4=6.2

        # 自定义动作空间，观察空间
        self.action_space = spaces.Box(
            # 羊的动作空间即为转动的角度，会根据当前位置进行变化
            # 由于怕出现low比high还大的情况，我们的action_space就不做周期处理，用的时候取余2pi就行
            low=0, high=2*np.pi, shape=(1,), dtype=np.float32
        )
        self.observation_space = spaces.Box(
            # 状态空间为 theta_E,R_E,theta_P
            low=np.array([0,0,0,0])
            ,high=np.array([2*np.pi,self.R,2*np.pi,2*np.pi])
            ,dtype=np.float32
        )
    '''
    羊接受一个动作进行位移: 使用PG算法的choose_action
    犬沿劣弧进行位移
    接着判断游戏是否结束
    评价这个动作的回报
    '''
    def step(self, action):# u为action
        # print('action: ',action)
        # 根据action（即θ_E'来计算新的状态）
        self.state = self._get_observation(action)
        reward = self._get_reward()
        done = self._get_done()
        if done:# 如果逃脱失败，给予惩罚
            if catch(self.R,self.state[0],self.state[2],self.state[3]):
                reward=reward-1000
                print('be catched')
            else:
                reward=0
                print('no be catched')
        return self.state,reward,done

    # 获取reward,根据action作用之后的state来计算reward
    def _get_reward(self):
        # thetaP=self.state[2]
        # thetaP2=self.state[3]
        # thetaE=self.state[0]
        thetaE,thetaP,thetaP2=self.state[0],self.state[2],self.state[3]
        delta_theta1=cal_angel(thetaE,thetaP)# 羊与犬1的夹角
        delta_theta2=cal_angel(thetaE,thetaP2)# 羊与犬2的夹角
        delta_theta3=cal_angel(thetaP,thetaP2)# 两犬之间的夹角
        # a=self.state[1]
        # b=self.R
        # distance=math.sqrt(a*a+b*b-2*a*b*np.cos(delta_theta))
        # 羊距圆周越近越好(radiusE越大越好)，羊与犬的夹角越大越好,羊离犬越远越好
        # print('r1: ',self.lambda1 * abs(self.R - self.state[1]))
        # print('r2: ',self.lambda2 * abs(np.pi-delta_theta1))
        # print('r3: ',self.lambda3 * abs(np.pi-delta_theta2))
        # print('r4: ',self.lambda4 * abs(delta_theta3))
        return -(# 想要趋近于零
                self.lambda1 * abs(self.R - self.state[1])# 范围 [0-2*R(200)]
                + self.lambda2 * abs(np.pi-delta_theta1) # 范围 [0-100]
                + self.lambda3 * abs(np.pi-delta_theta2) # 范围 [0-100]
                + self.lambda4 * abs(delta_theta3)   # 范围 [0-100]
        )

    # 判断游戏是否结束
    def _get_done(self):
        if self.state[1]>=self.R:
            return True
        else:
            return False
    # 根据action修改环境，改变状态
    def _get_observation(self,action):
        # 已知现在的位置，首先计算位移后羊的极坐标
        xb=self.state[1]*np.cos(self.state[0])+self.vE*self.dt*np.cos(action)
        yb=self.state[1]*np.sin(self.state[0])+self.vE*self.dt*np.sin(action)
        new_radiusE=math.sqrt(xb*xb+yb*yb)
        # 由xb和yb进行θ转换,# 返回弧度pi
        new_thetaE=math.atan2(yb,xb)
        new_thetaE=(new_thetaE+2*np.pi)%(2*np.pi)
        # 根据羊的action，选择狼的位移方向并位移
        delta_theta=self.wP*self.dt
        thetaE = self.state[0]
        # 修改犬1的状态
        thetaP = self.state[2]# 犬1的原状态
        new_thetaP=change_dog_state(thetaP,thetaE,delta_theta)# 犬1的新状态
        # 修改犬2的状态
        thetaP2 = self.state[3]  # 犬1的原状态
        new_thetaP2 = change_dog_state(thetaP2, thetaE, delta_theta)  # 犬1的新状态
        # 相等的话就保持原状态
        return np.array([new_thetaE,new_radiusE,new_thetaP,new_thetaP2])

    # 重置羊和犬的状态
    def reset(self):
        thetaE=random.uniform(0, 2 * np.pi)
        thetaE2=(thetaE+np.pi)%(2*np.pi)
        self.state=np.array([0,0,thetaE,thetaE2],dtype=float)
        return np.array(self.state)

    # 画画显示犬和羊的状态
    def render(self):
        # 清空轨迹
        # self.viewer.geoms.clear()
        # 绘制大圆
        ring = rendering.make_circle(radius=self.R,res=50,filled=False)
        transform1 = rendering.Transform(translation=(200, 200))  # 相对偏移
        ring.add_attr(transform1)# 让圆添加平移这个属性
        self.viewer.add_geom(ring)

        # 绘制犬1
        xP,yP=self.R*np.cos(self.state[2]),self.R*np.sin(self.state[2])
        ringP = rendering.make_circle(radius=2, res=50, filled=True)
        ringP.set_color(0,0,1)
        transform_P = rendering.Transform(translation=(200+xP, 200+yP))  # 相对偏移
        ringP.add_attr(transform_P)  # 让圆添加平移这个属性
        self.viewer.add_geom(ringP)
        # 绘制犬2
        xP2, yP2 = self.R * np.cos(self.state[3]), self.R * np.sin(self.state[3])
        ringP2 = rendering.make_circle(radius=2, res=50, filled=True)
        ringP2.set_color(0, 0, 1)
        transform_P2 = rendering.Transform(translation=(200 + xP2, 200 + yP2))  # 相对偏移
        ringP2.add_attr(transform_P2)  # 让圆添加平移这个属性
        self.viewer.add_geom(ringP2)

        # 绘制羊
        xE, yE = self.state[1] * np.cos(self.state[0]), self.state[1] * np.sin(self.state[0])
        ringE = rendering.make_circle(radius=2, res=50, filled=True)
        ringE.set_color(1, 0, 0)
        transform_E = rendering.Transform(translation=(200+xE, 200+yE))  # 相对偏移
        ringE.add_attr(transform_E)  # 让圆添加平移这个属性
        self.viewer.add_geom(ringE)

        return self.viewer.render()

# env = dogSheepEnv()
# while True:
#     env.reset()
#     for _ in range(2000):
#         env.render()
#         action=random.uniform(0,2*np.pi)
#         action=np.clip(action,env.state[0]-np.pi/2,env.state[0]+np.pi/2)
#         action=(action+2*np.pi)%(2*np.pi)
#         state, reward, done = env.step(action) # 和环境交互
#         if done:
#             break

2.3 题解结果

一犬一羊情况，回报收敛的趋势图

羊的逃逸路径

犬的追捕极角

羊的逃逸极角

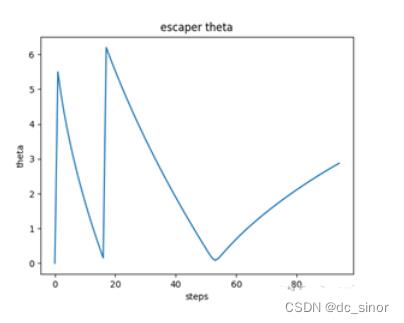
推广：两犬一只羊情况

回报收敛的趋势图

羊的逃逸路径

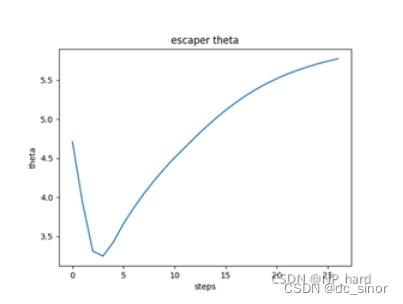
羊的逃逸极角

建模资料，获奖秘籍： https://gitee.com/math-sinor/math-data/blob/master/README.md