增量型算式 小算法

Posted 2022-06-25 资质平庸的程序员

1 微分方程的差分化

        用程序来计算方程的解，唯一可采用的方法使用数值法不断的逼近连续解，使两相邻数值解之间的间隔可以忽略不计从而近似为连续解，在一般情况下，采用较高精度的数值解就能够代替真实的解。如微分方程的四阶龙格库塔方法求解。[^-^在成长的过程中难免发表点感叹]为了记住给我留下深刻印象的增量表达式。还是要借助数字PID控制算法说事。这毕竟是留下记忆的载体。

PID控制器输出与输入的算式为：

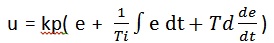
        这是一个含积分和微分的表达式，如果要编写程序来求解的话只能采用数值法了。为了用程序实现PID控制算式，采用“微元化的思想”(大一的高数)首先将微分方程改为差分方程：

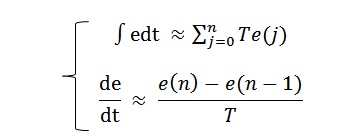
T为控制周期（很小很小的值，这样子才和连续值在同一时刻的值逼近），n为控制周期序号（n=0,1,2……）,e(n)表示第n控制周期所得的PID控制器的输入。将差分化的积分和微分表达式带入输出输入算式中得到：

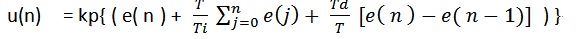
        简单的一个差分化思想，当然了如果不回味一下高数知识呢，稍微抽像一点点。

        以上表达式称为“位置型算式”。通过以上表达式可知，只要知道每次的e(n)(n =0, 1, 2…)就可以根据设定的采样周期和比例、积分、微分系数求得第n个时刻的输出。

      这个表达式对编写程序的人不利呀：原因是算式中要累加e(j)，不仅要占用很多的内存（一旦长时间运行起来n值将会多么大！上课时老师用计算器算了一下，2G内存不久就被占满了），而且直接也不利于编写程序代码。仔细想想就知道在编写程序时的确存在这两个问题。

 

2 用增量型表达式思想编程

        这种下一时刻跟上一时刻有关系的表达式在编写程序的时候总想用上一时刻的值来表达下一时刻的值，上一时刻（n - 1）的表达式为：

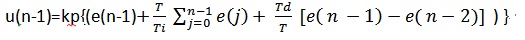
       用第n时刻的值与第n-1时刻的值差，得到差值:

n1=kp[ e(n) – e(n-1)] + (kp * T / Ti) * e(n) + (kp *Td / T)*[ e(n) + -2e(n-1) + e(n-2)]

第n时刻的值与第n-1时刻的值差值只跟相近的一两个输入e值有关系，是不是已经摆脱了n值过大时耗内存且不好编写程序的缺点呢。暂时是还不怎么好体会，先得u(n)的新表达式：

u(n) = u(n-1) +n1

     这个表达式看起来比前面的那几个表达式简单多了。结合n1的表达式其实用程序来实现的过程是这样子的：

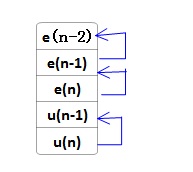
       用计算得到的新值去覆盖旧值，占用内存永远就那么大了（u(n)的值不超过对应数据类型表示范围的话，程序运行就不会出什么问题了）。无论是哪一种数值算法，初值都是不可少的。对于差分方程的初值解，可先按“位置型算式”求出直到能用上“增量型算式”的值，保存该保存的一些值。然后就可以采用循环计算数值了。

      然后凡是遇到累计和的，后项跟前项差是较少的跟可测变量值有关的表达式，就可以考虑用增量表达式小算法来解决问题。在对的时间和地点还是能解决大问题的。这毕竟是工业采用的方法。算法虽小，贡献甚大呀。

 

读《计算机控制》课本。

Note Over.