KNN算法及KNN的优化算法-加权KNN

Posted 2022-06-23 Terry_dong

KNN及加权KNN优化算法

深度学习的常规套路：

1.收集数据并给定标签
2.训练一个分类器
3.测试，评估

K-近邻(KNN)算法：

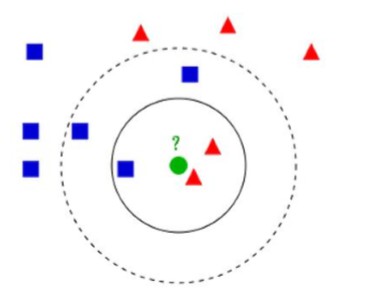
对于未知类别属性数据集中的点：
1.计算已知类别数据集中的点与当前点的距离
2.按照距离依次排序

3.选取与当前点距离最小的K个点
4.确定前K个点所在类别的出现概率
5.返回前K个点出现频率最高的类别作为当前点预测分类。
KNN算法：不需要使用训练集进行训练，训练复杂度为0，KNN分类的计算复杂度和训练集中的文档数目成正比。如训练集中文档总数为n，那么KNN的分类时间复杂度为O(n)。

例：CIFAR-10库采用KNN分类：

计算方法：

代码部分：

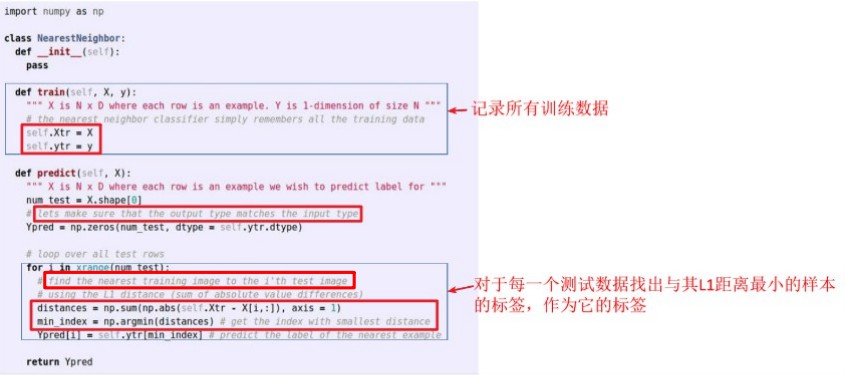
分类效果：

超参数(距离)：

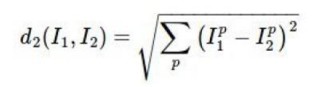
欧氏距离：应用勾股定理计算两个点的直线距离。

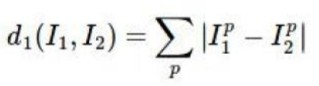
曼哈顿距离：表示两个点在标准坐标系上的绝对轴距之和。

调参-训练采用交叉验证：

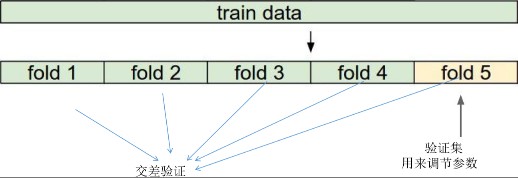
流程：

 

（一）训练集和测试集

训练集：
我的理解，训练集是一个集合，集合里面每一个元素分为两部份：

一部分是一个n维向量（也可能是矩阵之类的），也叫特征向量，就是特征空间里面的向量。
另一部分是一个标签，也就是每一类别的代号。

测试集：
测试集是从一堆测试样本中提取出来的特征向量的集合，它和训练集的区别在于它没有标签，而这个标签正是我们求解的目标。

（二）设定k的取值

这个问题很重要：
k太小，不具有抗干扰性，万一这几个最近的点有几个噪音怎么办？
k太大，不具有代表性，相当于用较大邻域中的训练实例进行预测，学习的近似误差会增大。
所以，经验来说：
一般k的取值不超过20，上限是n的开方，随着数据集的增大，K的值也要增大。
 

（三）距离

这个距离就有的说了。
怎样定义距离？
常见的有欧几里得距离、余弦值, 相关度 , 曼哈顿距离等

简单介绍一下吧：

1 欧几里得距离:
n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离（两个n维向量）：

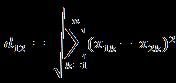
2 余弦值：
几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。
二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：

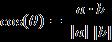
即：

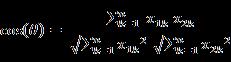
夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

3 相关系数
相关系数：是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）：

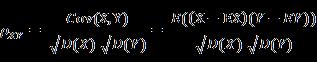
相关距离：

4 曼哈顿距离
n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离：

更多距离请移步：几种距离的度量方式
 

附：KNN算法实例：

样本数据：

KNN的脚本代码：

#!/usr/bin/python

coding=utf-8

#########################################

kNN: k Nearest Neighbors

输入:      newInput:  (1xN)的待分类向量

dataSet:   (NxM)的训练数据集

labels:     训练数据集的类别标签向量

k:         近邻数

输出:     可能性最大的分类标签

#########################################

from numpy import *

import operator

创建一个数据集，包含2个类别共4个样本

def createDataSet():

    # 生成一个矩阵，每行表示一个样本

    group = array([[1.0, 0.9], [1.0, 1.0], [0.1, 0.2], [0.0, 0.1]])

    # 4个样本分别所属的类别

    labels = ['A', 'A', 'B', 'B']

    return group, labels

KNN分类算法函数定义

def kNNClassify(newInput, dataSet, labels, k):

    numSamples = dataSet.shape[0]   # shape[0]表示行数
# # step 1: 计算距离[
# 假如：
# Newinput：[1,0,2]
# Dataset:
# [1,0,1]
# [2,1,3]
# [1,0,2]
# 计算过程即为：
# 1、求差
# [1,0,1]       [1,0,2]
# [2,1,3]   --   [1,0,2]
# [1,0,2]       [1,0,2]
# =
# [0,0,-1]
# [1,1,1]
# [0,0,-1]
# 2、对差值平方
# [0,0,1]
# [1,1,1]
# [0,0,1]
# 3、将平方后的差值累加
# [1]
# [3]
# [1]
# 4、将上一步骤的值求开方，即得距离
# [1]
# [1.73]
# [1]
#
# ]
# tile(A, reps): 构造一个矩阵，通过A重复reps次得到
# the following copy numSamples rows for dataSet
diff = tile(newInput, (numSamples, 1)) - dataSet  # 按元素求差值
squaredDiff = diff ** 2  # 将差值平方
squaredDist = sum(squaredDiff, axis = 1)   # 按行累加
distance = squaredDist ** 0.5  # 将差值平方和求开方，即得距离

# # step 2: 对距离排序
# argsort() 返回排序后的索引值
sortedDistIndices = argsort(distance)
classCount =  # define a dictionary (can be append element)
for i in xrange(k):
    # # step 3: 选择k个最近邻
    voteLabel = labels[sortedDistIndices[i]]

    # # step 4: 计算k个最近邻中各类别出现的次数
    # when the key voteLabel is not in dictionary classCount, get()
    # will return 0
    classCount[voteLabel] = classCount.get(voteLabel, 0) + 1

# # step 5: 返回出现次数最多的类别标签
maxCount = 0
for key, value in classCount.items():
    if value > maxCount:
        maxCount = value
        maxIndex = key

return maxIndex
1

KNN-TEST的测试代码：

#!/usr/bin/python
# coding=utf-8
import KNN
from numpy import *
# 生成数据集和类别标签
dataSet, labels = KNN.createDataSet()
# 定义一个未知类别的数据
testX = array([1.2, 1.0])
k = 3
# 调用分类函数对未知数据分类
outputLabel = KNN.kNNClassify(testX, dataSet, labels, 3)
print "Your input is:", testX, "and classified to class: ", outputLabel

testX = array([0.1, 0.3])
outputLabel = KNN.kNNClassify(testX, dataSet, labels, 3)
print "Your input is:", testX, "and classified to class: ", outputLabel

测试效果：

参考博客链接：

 https://www.cnblogs.com/ahu-lichang/p/7151007.html

KNN算法注意事项：
1.预处理你的数据：对你数据中的特征进行归一化（normalize），让其具有零平均值 （zero mean）和单位方差（unit variance）。
2.如果数据是高维数据，考虑使用降维方法，比如PCA。
3.将数据随机分入训练集和验证集。按照一般规律，70%-90% 数据作为训练集。
4.在验证集上调优，尝试足够多的k值，尝试曼哈顿距离和欧氏距离两种范数计算方式。

KNN算法缺陷及优化：

1.样本不平衡容易导致结果错误

如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。

改善方法：对此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。
2.计算量较大

因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。

改善方法：事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

该方法比较适用于样本容量比较大的类域的分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

加权KNN算法：

采用Gaussian函数进行不同距离的样本的权重优化，当训练样本与测试样本距离↑，该距离值权重↓。
给更近的邻居分配更大的权重(你离我更近，那我就认为你跟我更相似，就给你分配更大的权重)，而较远的邻居的权重相应地减少，取其加权平均。

加权KNN代码：

def gaussian(dist, sigma = 10.0):
    """ Input a distance and return it`s weight"""
    weight = np.exp(-dist**2/(2*sigma**2))
    return weight
 
### 加权KNN
def weighted_classify(input, dataSet, label, k):
    
    dataSize = dataSet.shape[0]
    diff = np.tile(input, (dataSize, 1)) - dataSet
    sqdiff = diff**2
    squareDist = np.array([sum(x) for x in sqdiff])
    dist = squareDist**0.5
    #print(input, dist[0], dist[1164])
    sortedDistIndex = np.argsort(dist)
 
    classCount = 
    for i in range(k):
        index = sortedDistIndex[i]
        voteLabel = label[index]
        weight = gaussian(dist[index]) 
        #print(index, dist[index],weight)
        ## 这里不再是加一，而是权重*1
        classCount[voteLabel] = classCount.get(voteLabel, 0) + weight*1
        
    maxCount = 0
    #print(classCount)
    for key, value in classCount.items():
        if value > maxCount:
            maxCount = value
            classes = key
            
    return classes

（一）加什么权？

1 反比例函数

weight = 1 / (distance + const)

完全一样或非常接近的权重会很大甚至无穷大。基于这样的原因，在距离求倒数时，在距离上加一个常量const。
这种方法的潜在问题是，它为近邻分配很大的权重，稍远一点的会衰减的很快。虽然这种情况是我们希望的，但有时候也会使算法对噪声数据变得更加敏感。

2 高斯函数
高斯函数比较复杂，但克服了前述函数的缺点，其形式：

其中a,b,c∈R
其图像为：

效果很好，能够克服缺点，最大也就顶点值，再小也不为0，因此可以一定程度上克服噪声带来的影响。

（二）怎么加权

将各个类预测的权重值相加，哪个类最大，就属于哪个类。

就是在对每一类计数的时候，加的不是1二是权重。

假如k=3
三个类别分别为A、A、B
一般来讲，A有2个，B有1个，那么判别结果为A

加权情况下，三个邻近的权重分别为A（0.8），A（0.6），B（0.5）
相当于最后有0.8+0.6=1.4（个）A，0.5（个）B，所以最后选A。

三、总结

1. kNN很简单，是数据分析、模式识别的基础和入门
2. kNN每预测一个新样本的所属类别时，都会对整体样本进行遍历，可以看出kNN的效率实际上是十分低下的。
3. 代码就不贴了，网上太多了，写下来也是提醒一下自己。