第三节1:类K-Means算法之K-中心点(K-Medoid)和PAM算法
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第三节1:类K-Means算法之K-中心点(K-Medoid)和PAM算法相关的知识,希望对你有一定的参考价值。
文章目录
一:原始K-中心点算法
(1)算法思想
k k k-中心点算法:在 k k k- m e a n s means means算法中,中心点会被设定为当前簇中所有数据点的平均值,而这个平均值极大可能是不包含在初始数据集中的,也即它是一个虚拟的点。但在 k k k-中心点算法中,选取的是到当前簇中所有其他数据点的距离之和最小的点作为这一簇的中心点,这个点一定是在初始数据集中包含的点中选取的。相比于簇均值,真实的数据点受到离群点的影响会更小一些,因此该种算法对数据集中存在的噪声点和离群点有着更强的鲁棒性
该算法以绝对误差和作为算法的目标函数
E ( C ) = ∑ k = 1 K ∑ x i ∈ C k ∣ x i − c k ∣ E(C)=\\sum_k=1^K\\sum_x_i\\in C_k|x_i-c_k| E(C)=k=1∑Kxi∈Ck∑∣xi−ck∣
(2)算法流程
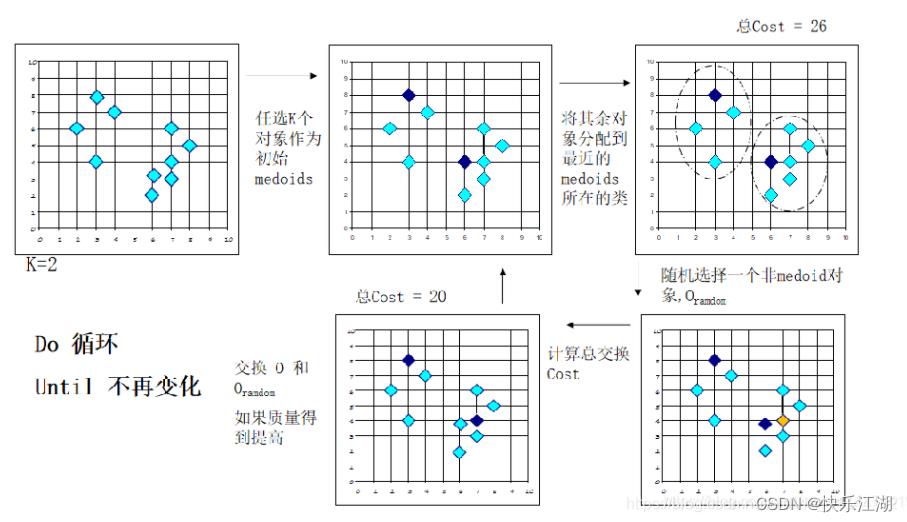
k k k-中心点算法流程:该算法首先从每个簇中随机选择一个对象作为代表对象,然后将其余非代表对象按照其与已选择的代表对象之间的距离来将其分配给最近的一个代表对象所属的簇。通过反复尝试使用非代表对象来代替当前代表对象可以改进聚类的整体质量

在替换代表对象时,对于每一个非代表对象 p p p,考虑以下四种情况
-
情况一: p p p当前从属于代表对象 O f O_f Of的簇,如果 O f O_f Of被 O r O_r Or代替,且 p p p距离 O i O_i Oi最近, i ≠ f i\\neq f i=f,那么 p p p将会被重新分配给 O i O_i Oi
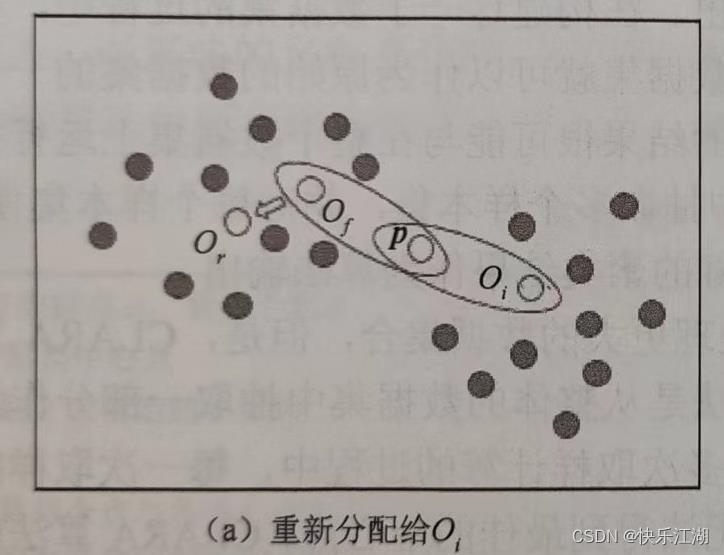
-
情况二: p p p当前从属于代表对象 O f O_f Of的簇,如果 O f O_f Of被 O r O_r Or代替,且 p p p距离 O r O_r Or最近,那么 p p p将会被重新分配给 O r O_r Or
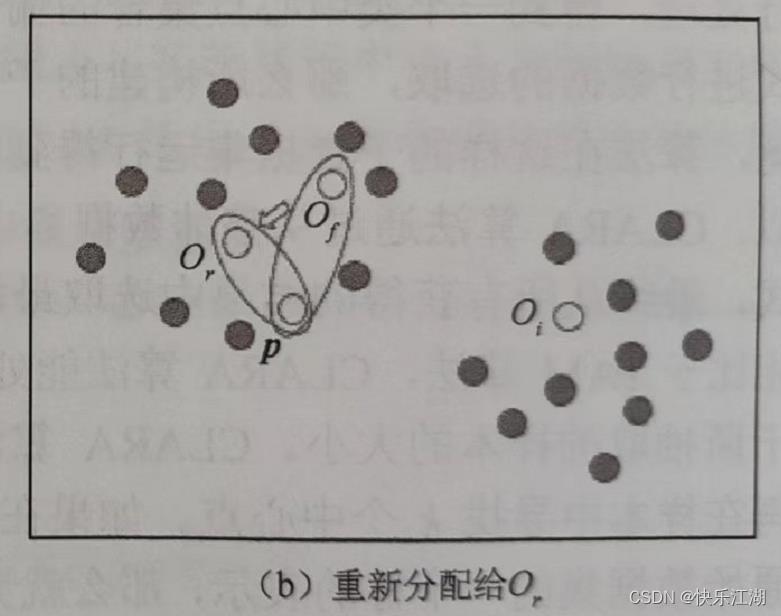
-
情况三: p p p当前从属于代表对象 O i O_i Oi的簇, i ≠ f i\\neq f i=f,如果 O f O_f Of被 O r O_r Or代替,且 p p p距离 O i O_i Oi仍最近,那么 p p p的从属不会发生变化
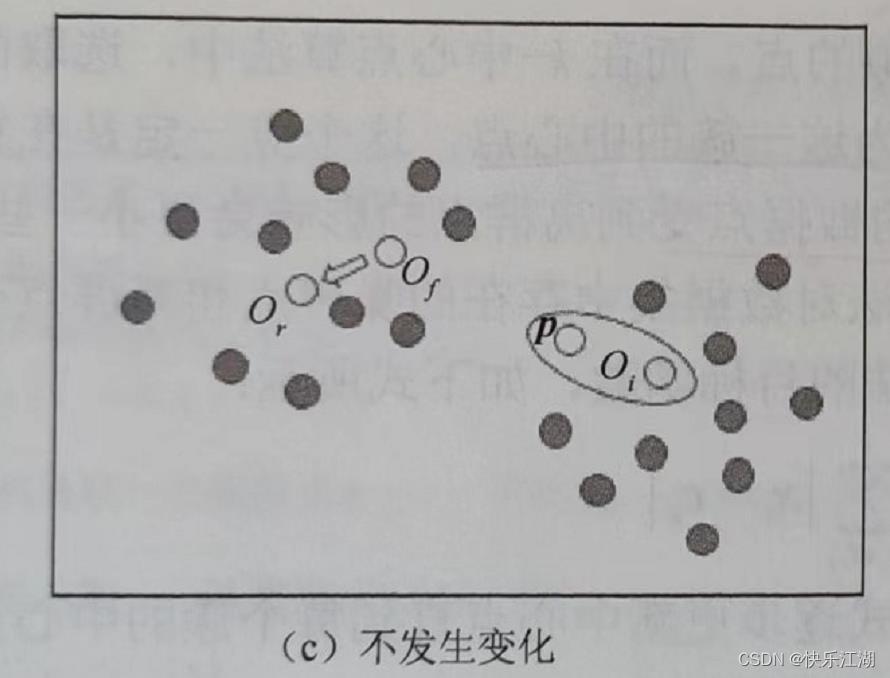
-
情况四: p p p当前从属于代表对象 O i O_i Oi的簇, i ≠ f i\\neq f i=f,如果 O f O_f Of被 O r O_r Or代替,且 p p p距离 O r O_r Or最近,那么 p p p将会被重新分配给 O r O_r Or
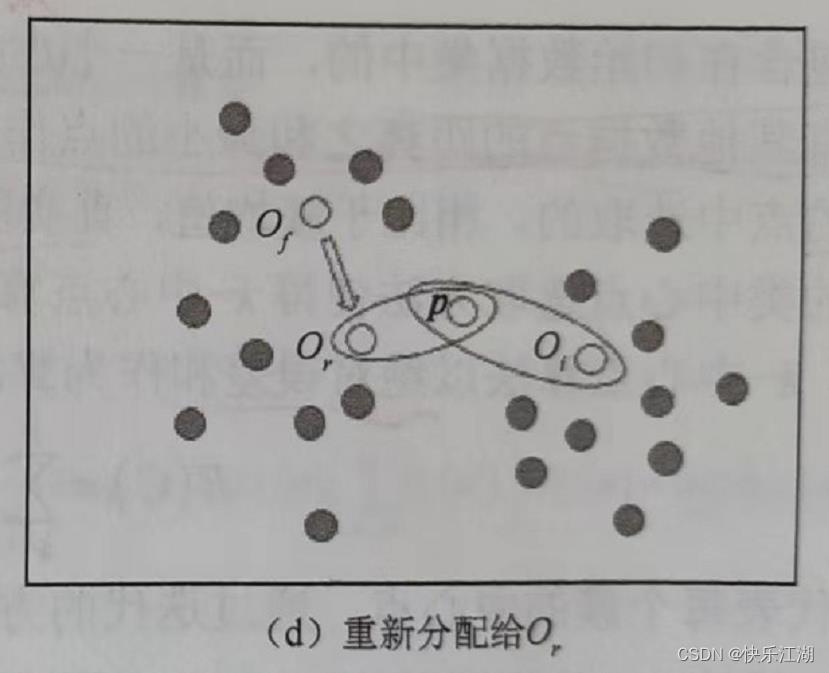
(3)Python实现
- 这里在上节 K K K- M e a n s Means Means++算法的基础上进行修改
import numpy as np
import sys
import random
'''
1.一开始也是随机选择K个初始对象
2.将每个剩余的对象分配在临近的簇中当中去,计算当前代价
3.随机选择一个非质心对象作为新质心
4.计算用新质心的总代价S
5.If S <旧质心, t就替换用当前质心代替旧质心,形成新的k个簇重复整个过程 直到质心位置不在发生变化。
'''
# 借助K-Means++算法选择出质心,然后只进行一次划分
# 计算最短距离
def nearest(point, centorids):
min_dist = sys.float_info.max
m = np.shape(centorids)[0] # 已经初始化的聚类中心个数
for i in range(m):
# 计算该点与每个聚类中心之间的距离
dist = np.sqrt(np.sum(np.power(point - centorids[i, ], 2)))
# 选择最短距离
if min_dist > dist:
min_dist = dist
return min_dist
# k-means++获取初始中心点
def get_centorids(data_set, k):
m, n = np.shape(data_set)
centorids = np.zeros((k, n))
# 1.随机选取一个样本点作为第一个聚类中心
index = np.random.randint(0, m)
centorids[0, ] = np.copy(data_set[index, ]) # 第一个聚类中心
# 2.初始化一个聚类序列
dist = [0.0 for _ in range(m)]
for i in range(1, k):
sum_all = 0
for j in range(m):
# 3.对每一个样本找到其最近的聚类中心点
dist[j] = nearest(data_set[j, ], centorids[0:i, ])
# 4.将所有的最短距离相加
sum_all += dist[j]
# 5.取一个位于sum_all之间的随机值
R = sum_all * np.random.random() # 随机值R
for j, di in enumerate(dist):
# 6.重复计算R=R-D(X)直到R小于等于0,此时的样本点可以作为聚类中心点
R -= di
if R > 0:
continue
centorids[i] = np.copy(data_set[j, ])
break
return centorids
# 用于判断质心是否发生了变换
def chech_if_change(current_centorids, pre_centorids):
if current_centorids.all() == pre_centorids.all():
return True
else:
return False
# 计算距离实现划分
def compute_cluster(data_set, centorids, E):
examples_nums = np.shape(data_set)[0] # 样本数量
centorids_nums = np.shape(centorids)[0] # 质心数量
cluster = np.zeros((examples_nums, 1)) # 返回结果
for examples_index in range(examples_nums):
distance = np.zeros(centorids_nums) # 保存examples_index这个样本点到各质心点的距离
for centorids_index in range(centorids_nums):
distance[centorids_index] = np.sqrt(np.sum(
np.power(data_set[examples_index, :]-centorids[centorids_index, :], 2)))
cluster[examples_index] = np.argmin(distance) # 最终在这些距离中选择出最小的一个
E[examples_index] = min(distance)
return cluster, E
# 用于更新质心
def renew_centoids(data_set, cluster, k, E, centorids):
rs = np.random.RandomState(2) # 随机种子
for centroid_id in range(k):
temp = data_set[(cluster == centroid_id).flatten(), :]
noncenter_ids = np.argwhere(temp)
randid = rs.choice(noncenter_ids[0], 1)
point =data_set[randid, :] # 随机选取一个非代表点
# 计算代价
origin_cost = np.sum(E[(centroid_id == cluster).flatten()]) # 原始代价
new_cost = E[randid] # 新的代价
for j in range(len(noncenter_ids)):
other_point = data_set[noncenter_ids[j], :]
new_cost += np.sqrt(np.sum(np.power(point-other_point, 2)))
S = new_cost - origin_cost
if S < 0:
centorids[centroid_id] = point
cluster[centroid_id] = randid
return cluster, centorids
# 算法主体
def k_medoid(data_set, k, max_iterations):
examples_nums = np.shape(data_set)[0] # 样本数量
centorids = get_centorids(data_set, k) # 随机选取k个质心
cluster = np.zeros(examples_nums) # 用于标识该样本点与那个质心最近,其本质就是划分的簇
E = np.empty(examples_nums) # 距离
for _ in range(max_iterations): # 不断迭代
pre_centorids = centorids.copy() # 更新质心前保存副本,用于判断质心是否发生变化
# 计算距离且分配
cluster, E = compute_cluster(data_set, centorids, E)
# 更新质心
cluste以上是关于第三节1:类K-Means算法之K-中心点(K-Medoid)和PAM算法的主要内容,如果未能解决你的问题,请参考以下文章