C++进阶红黑树

Posted 2022-06-16 Huang_ZhenSheng

目录

红黑树的性质

新增节点问题

情况一：cur为红，p为红，g为黑，u存在且为红

情况二：cur为红，p为红，g为黑，u不存在/u存在且为黑（单旋）

情况三：cur为红，p为红，g为黑，u不存在/u存在且为黑（双旋）

红黑树完整代码：Gitee

红黑树的性质

1，每个节点不是红色就是黑色

2，根节点是黑色的

3，如果一个节点是红色的，则它的两个孩子节点必须是黑色的

4，对于每个节点，从该结点到其所有后代叶结点的简单路径上，都包含相同数目的黑色结点

5，每个叶子结点都是黑色的（此处的叶子结点指的是空节点）

新增节点问题

如果新增一个节点就新增一个红色节点：

1，如果新增节点的父亲是黑色，则不需要处理

2，如果新增节点的父亲是红色，则产生了连续的红色节点，需要分情况处理：

情况一：cur为红，p为红，g为黑，u存在且为红

情况二：cur为红，p为红，g为黑，u不存在/u存在且为黑（单旋）

情况二-1：u不存在，那么cur就是新增

情况二-2：u存在且为黑的情况下，cur一定不是新增

情况三：cur为红，p为红，g为黑，u不存在/u存在且为黑（双旋）

情况三-1：u不存在，那么cur就是新增

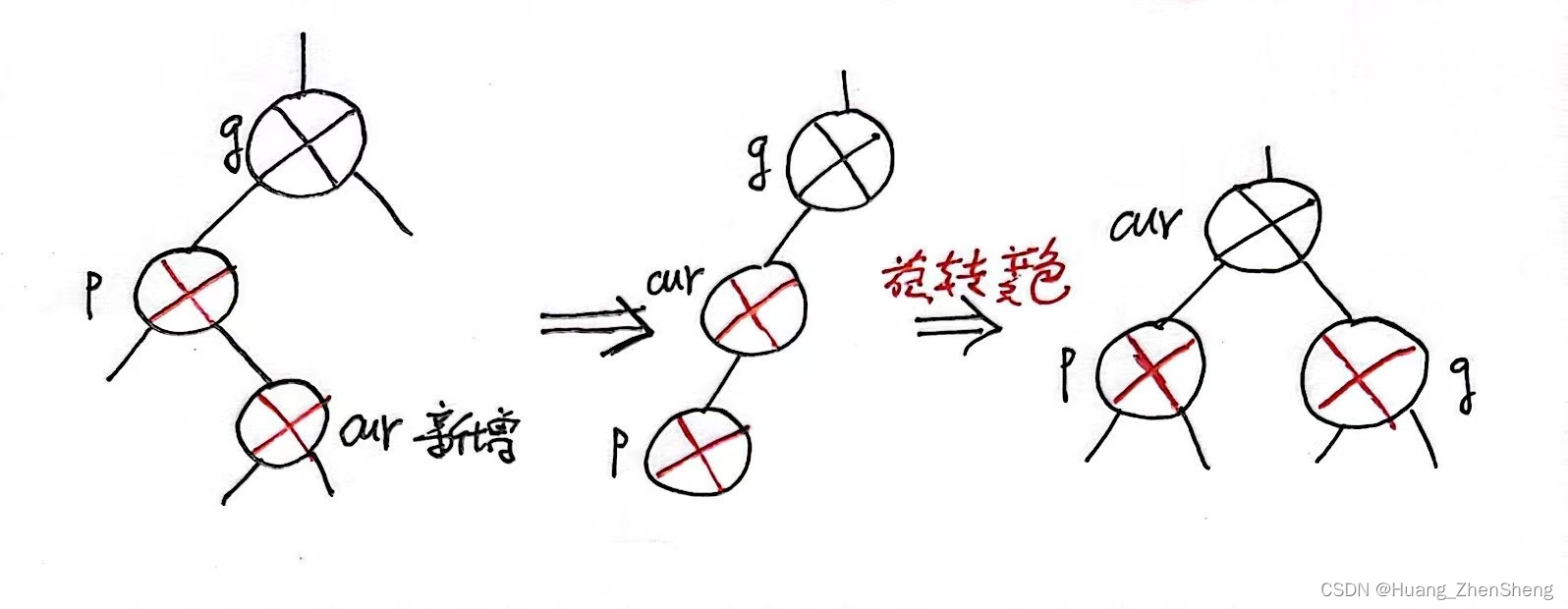
情况三-2：u存在且为黑的情况下，cur一定不是新增

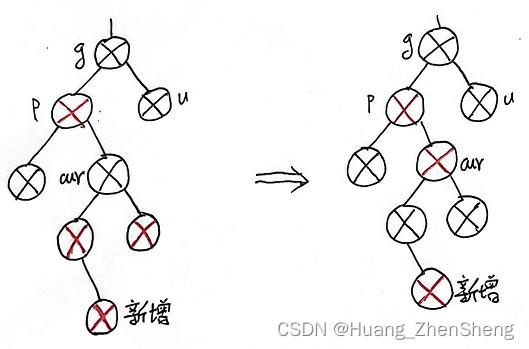
==》回归到情况三-1

将以上的图转换为代码如下：（代码中的旋转代码详见上一章的AVLTree）

while (parent && parent->_col == RED)
		
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			
				Node*uncle = grandfather->_right;
				//情况一:uncle存在且为红，进行变色处理即可,并且继续往上更新处理
				if (uncle && uncle->_col == RED)
				
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;
					//继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				
				//情况二+三:uncle不存在，或者存在且为黑，需要旋转+变色处理
				else
				
					//情况二:单旋+变色
					if (cur == parent->_left)
					
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					
					//情况三:双旋+变色
					else
					
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					
					break;
				
			
			else //parent == grandfather->_right
			
				Node*uncle = grandfather->_left;
				//情况一:uncle存在且为红，进行变色处理即可,并且继续往上更新处理
				if (uncle && uncle->_col == RED)
				
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;
					//继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				
				//情况二+三:uncle不存在，或者存在且为黑，需要旋转+变色处理
				else
				
					//情况二:单旋+变色
					if (parent->_right == cur)
					
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					
					//情况三:双旋+变色
					else
					
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					
					break;
				
			
		
		_root->_col = BLACK;
		return true;
	

如何判断红黑树是否平衡IsBalance？

难点：如果判断每条路径均包含相同数目的黑色结点？

==》先取一个基准值，然后进行对比

bool Check(Node* root)
	
		if (root == nullptr)
		
			return true;
		
		if (root->_col == RED && root->_parent->_col == RED)
		
			cout << "存在连续的红色节点" << endl;
			return false;
		
		return Check(root->_left)
		&& Check(root->_right);
	
//较难！
	//检查每条路径黑色结点的数目
	bool Check_BLACK(Node* root, int blackNum, int benchmark)
	
		if (root == nullptr)
		
			if (blackNum != benchmark)
			
				cout << "黑色结点的数目不相等" << endl;
				return false;
			
			return true;
		
		if (root->_col == BLACK)
		
			blackNum++;
		
		return Check_BLACK(root->_left, blackNum, benchmark)
			&& Check_BLACK(root->_right, blackNum, benchmark);
	
	bool IsBalance()
	
		if (_root == nullptr)
		
			return true;
		
		if (_root->_col == RED)
		
			cout << "根节点是红色" << endl;
			return false;
		
		//算出最左路径的黑色结点的数量作为基准值
		int benchmark = 0;
		Node* cur = _root;
		while (cur)
		
			if (cur->_col == BLACK)
			
				benchmark++;
			
			cur = cur->_left;
		
		int blackNum = 0;
		return Check(_root) && Check_BLACK(_root,blackNum,benchmark);
	

红黑树完整代码：Gitee