论文笔记|深读struc2vec: Learning Node Representations from Structural Identity
Posted 海轰Pro
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文笔记|深读struc2vec: Learning Node Representations from Structural Identity相关的知识,希望对你有一定的参考价值。
目录

前言
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
知其然 知其所以然!
本文仅记录自己感兴趣的内容
ABSTRACT
结构标识是一种对称概念,根据网络结构及其与其他节点的关系来标识网络节点
本文提出了一种新的、灵活的框架struc2vec,用于学习节点结构身份的潜在表示。Struc2vec使用层次结构来度量不同尺度上的节点相似性,并构建一个多层图来编码结构相似性,为节点生成结构上下文。
实验表明,学习节点表示的最先进技术无法捕获更强的结构身份概念,而struc2vec在这项任务中表现出更优越的性能
1. INTRODUCTION
在几乎所有的网络中,节点往往具有一种或多种功能,这些功能在很大程度上决定了它们在系统中的角色
可以根据节点在网络中的作用将其划分为等价类
最常见的实用方法来确定节点的结构身份是基于距离或递归
- 基于
距离:使用一个利用节点邻域的距离函数来测量所有节点对之间的距离,然后进行聚类或匹配,将节点放入等效类中
-基于递归: 构造一个关于相邻节点的递归,然后迭代展开,直到收敛,用最后的值来确定等价类
这些方法各有利弊,但我们提供了一种替代方法:一种基于对节点的结构标识表示的无监督学习的方法。
最近 一些 学习网络中节点的潜在表示(网络嵌入) 的方法(DeepWalk、 node2vec)在执行分类和预测任务方面取得了成功:将节点编码为上下文,使用其邻域的广义概念(随机游走一定的步数,或有共同邻域的节点)。
==> 具有相似节点集的邻域的节点应该具有相似的潜在表示
若一些节点的领域中的节点集很相似,则这些节点应该具有相似的潜在表示
但存在一个问题:尽管两个节点的领域结构相似,但相距很远,所以不会有相似的潜在表示。
下图可以说明这个问题:
- 其中节点 u u u和 v v v具有类似的局部结构,但在网络中相距很远
- 由于它们的邻域没有公共节点,DeepWalk、 node2vec等方法则不能捕捉它们的结构相似性
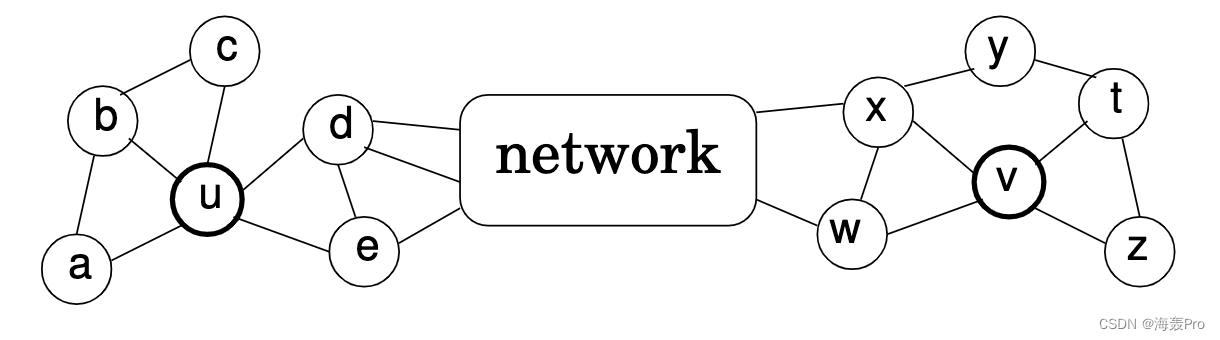
为什么最近一些学习节点表示的方法,如DeepWalk[16]和node2vec[6],在分类任务中成功,但在结构等价任务中往往失败

struc2vec
- 一个可扩展的框架
- 用于学习节点结构身份的潜在表示
struc2vec关键思想:
- Assess structural similarity between nodes independently of node and edge aŠributes as well as their position in the network
- Establish a hierarchy to measure structural similarity, allowing progressively more stringent notions of what it means to be structurally similar
- Generates random contexts for nodes, which are sequences of structurally similar nodes as observed by a weighted random walk traversing a multilayer graph (and not the original network).
2. RELATED WORK
DeepWalk
Learning a language model from a network was first proposed by DeepWalk [ 16 ]. It uses random walks to generate sequences of nodes from the network, which are then treated as sentences by Skip-Gram.
node2vec
Intuitively, nodes close in the network will tend to have similar contexts (sequences) and thus have embeddings that are near one another. this idea was later extended by node2vec
By proposing a biased second order random walk model, node2vecprovides more ƒexibility when generating the context of a vertex. In particular, the edge weights driving the biased random walks can be designed in an aŠempt to capture both vertex homophily and structural equivalence
DeepWalk和node2vec的缺点
如果结构相似的节点的距离(跳数)大于Skip-Gram窗口,则它们永远不会共享相同的上下文
subgraph2vec
subgraph2vec [ 14] is another recent approach for learning embeddings for rooted subgraphs, and unlike the previous techniques it does not use random walks to generate context. Alternatively, the context of a node is simply de€ned by its neighbors. Additionally,subgraph2vec captures structural equivalence by embedding nodes with the same local structure to the same point in space. Nonetheless, the notion of structural equivalence is very rigid since it is de€ned as a binary property dictated by the Weisfeiler-Lehman isomorphism test [ 21]. Œus, two nodes that are structurally very similar (but fail the test) and have non-overlapping neighbors may not be close in space.
Subgraph2vec[14]是另一种最近用于学习有根子图的嵌入的方法,与之前的技术不同,它不使用随机漫步来生成上下文。或者,一个节点的上下文只是由它的邻居确定。此外,subgraph2vec通过将具有相同局部结构的节点嵌入空间中的同一点来捕获结构等价性。尽管如此,结构等价的概念是非常严格的,因为它被定义为由Weisfeiler-Lehman同构检验[21]所规定的二元性质。对于我们来说,两个在结构上非常相似(但没有通过测试)且具有非重叠邻居的节点在空间上可能并不相近。
RolX
this is unsupervised approach is based on enumerating various structural features for nodes, finding the more suited basis vector for this joint feature space, and then assigning for every node a distribution over the identi€ed roles (basis), allowing for mixed membership across the roles. Without explicitly considering node similarity or node context (in terms of structure), RolX is likely to miss node pairs that are structurally equivalent.
这种无监督的方法是基于枚举节点的各种结构特征,为该联合特征空间找到更适合的基向量,然后为每个节点分配在已识别的角色(基)上的分布,允许跨角色的混合成员。没有明确考虑节点相似性或节点上下文(根据结构),RolX很可能会错过结构上等价的节点对
3. STRUC2VEC
对于捕获网络中节点的结构身份的学习表示,一个有效的方法应具备:
- 节点的潜在表征( latent representation)之间的距离应该与节点的结构相似性密切相关。
- 具有相同局域网结构的两个节点应该具有相同的潜在表示
- 而具有不同结构身份的节点 应该相距很远(这里的距离是指节点latent representation之间的距离)
- 潜在表示不应该依赖于任何节点或边缘属性,包括节点标签
- 因此,在结构上相似的节点应该有紧密的潜在表示,独立于节点和边缘的属性。
- 节点的结构身份必须独立于其在网络中的“位置”
struct2vec框架的四个步骤:
-
对于不同的邻域大小,确定图中每个顶点对之间的结构相似性
在度量节点之间的结构相似度时引入了层次,提供了更多的信息来评估层次的每一层的结构相似度
-
构造一个加权多层图
网络中的所有节点都存在于每一层,每一层对应于层次的一个层次,用于度量结构相似性
每层内每个节点对之间的边权值与它们的结构相似度成反比
-
使用多层图为每个节点生成上下文
在多层图上使用有偏随机游走,用来生成节点序列
结构上更相似的节点更大概率会在这些序列中
-
应用一种技术,从节点序列给出的上下文学习潜在表示,例如SkipGram
和deepwalk一样,利用这些序列进行学习
struct2vec is quite flexible as it does not mandates any particular structural similarity measure or representational learning framework.
struct2vec是相当灵活的,因为它不要求任何特定的结构相似性测量或表征学习框架
3.1 Measuring structural similarity
struct2vec的第一步是在不使用任何节点或边的情况下确定两个节点之间的结构相似性
此外,这种相似性度量应该是分层的,并应对不断增加的邻域大小,捕捉更多的结构相似性概念。
直观地说,具有相同度的两个节点在结构上是相似的,但是如果它们的相邻节点也具有相同的度,那么它们在结构上更加相似
k ∗ k^* k∗: 图 G G G的直径
图的直径是指任意两个顶点间距离的最大值.(距离是两个点之间的所有路的长度的最小值
R k ( u ) R_k(u) Rk(u): 顶点u经过k跳到达的图中顶点的集合
R 1 ( u ) R_1(u) R1(u)表示节点u的邻域(与节点u相邻的节点的集合)
s ( S ) s(S) s(S): 节点集合的有序度序列(按照节点的度进行排列)
S是一个节点集合,含有多个集合,s(S)就是对S中的结点再按照度大小进行排序
通过比较 s ( R k ( u ) ) s(R_k(u)) s(Rk(u))和 s ( R k ( v ) ) s(R_k(v)) s(Rk(v)),我们可以建立一个层次来衡量结构相似性。
一共有k层,第一层比较 s ( R 1 ( u ) ) s(R_1(u)) s(R1(u))和 s ( R 1 ( v ) ) s(R_1(v)) s(R1(v)),第二层比较 s ( R 2 ( u ) ) s(R_2(u)) s(R2(u))和 s ( R 2 ( v ) ) s(R_2(v)) s(R2(v))…
f k ( u , v ) f_k(u,v) fk(u,v): 顶点u和顶点v之间的结构距离(第k层中)
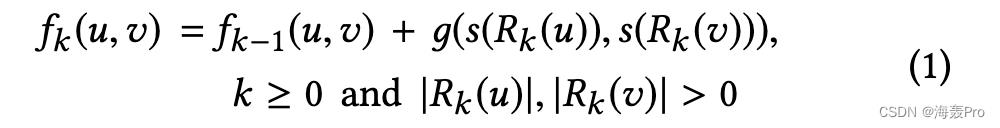
- D 1 , D 2 D_1,D_2 D1,D2:有序度序列,就是 s ( S ) s(S) s(S)
- g ( D 1 , D 2 ) g(D_1, D_2) g(D1,D2): 表示有序度序列 D 1 D_1 D1和 D 2 D_2 D2之间的距离, g ( D 1 , D 2 ) ≥ 0 g(D_1, D_2) \\geq 0 g(D1,D2)≥0 且 f − 1 = 0 f_-1=0 f−1=0
- f k ( u , v ) f_k(u,v) fk(u,v)递增,且只有当节点u和v之间都存在k跳时 f k ( u , v ) f_k(u,v) fk(u,v)才有意义
- 如果节点u和v的 k跳邻域同构,则可以将u映射为v,令 f k − 1 ( u , v ) = 0 f_k-1(u, v) = 0 fk−1(u,v)=0
确定比较两个度序列 s ( S ) s(S) s(S)的函数 g ( s 1 , s 2 ) g( s_1, s_2 ) g(s1,s2) ==> 采用动态时间规整(Dynamic Time Warping, DTW)来测量两个有序度序列之间的距离
假设有两个有序度序列 A , B A, B A,B
DTW将元素a与b进行匹配 ( a ∈ A , b ∈ B ) (a∈A, b∈B) (a∈A,b∈B),使匹配元素之间的距离之和最小
图中两个顶点之间的距离怎么定义呢?(这里的距离是指匹配DTW算法中的距离)
定义顶点a,b之间的距离为
d ( a , b ) = m a x ( a , b ) m i n ( a , b ) − 1 d(a, b) = \\fracmax(a,b)min(a, b) - 1 d(a,b)=min(a,b)max(a,b)−1
- 当 a = b a =b a=b时, d ( a , b ) = 0 d(a, b) = 0 d(a,b)=0 ==> 两个相同的有序度序列的距离为零
3.2 Constructing the context graph
我们需要构造一个多层加权图来编码节点之间的结构相似性
- G G G: 原始图
-
M
M
M: 多层加权图(无向),层数为
k
k
k
- k = 0 , 1 , . . . k ∗ k =0, 1,... k^* k=0,1,...k∗
- k ∗ k^* k∗是图的直径
每一层有 n ( n = ∣ V ∣ ) n(n= |V|) n(n=∣V∣)个节点, C n 2 C_n^2 Cn2条边
第k层中,两个节点之间的边权重定义为
w k ( u , v ) = e − f k ( u , v ) , k = 0 , 1 , . . . k ∗ w_k(u, v) = e^-f_k(u,v), k =0, 1,... k^* wk(u,v)=e−fk(u,v),k=0,1,...k∗
- 上式仅当