动态规划之最长公共子串
Posted 清风明月coder
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划之最长公共子串相关的知识,希望对你有一定的参考价值。
一 问题引入
在生物学中,经常需要比较两个不同生物的DNA,一个DNA串由由一串称为碱基的的分子组成,碱基有鸟嘌呤,腺嘌呤,胞嘧啶,胸腺嘧啶四中,我们用英文字母的首字母表示四种碱基,那么DNA就是在有限集A,C,G,T上的一个字符串。例如某种生物的DNA序列为:S1=ACCGGTCGAGTGCGCGGAAGCCGGCCGAA,S2=GTCGTTCGGAATGCCGTTGCTCTGTAAA,我们比较两个DNA串的原因就是希望确定他们的相似度,作为衡量两个物种相似度的标准。如果一个串是另外一个串的子串,那么它们就是相似的,但是这里彼此都不是彼此的子串。于是我们就有了新的衡量标准:寻找一个新串S3,使得S3中的元素都在S1,S2中出现过,且不要求连续,但是碱基在三个串中出现的顺序一定要相同。可以找到的S3的长度越长,表明两个物种越相似!
二 问题描述
给定两个字符串X[A,B,C,B,D,A,B]和Y[B,D,C,A,B,A],求X和Y的最长公共子序列LCS
三 思路
1 采用暴力破解法: 扫描X所有的可能子串, 取其中一个字符时候,存在 取或不取两种情况, 假设X字符串有M个字符,则子串个数为2的M次方,
假设Y有N个字符,将M中取出的子串与Y中进行对比,最后的时间复杂度为 N*2^M, 简直是龟速啊。。。
2 简化方案
2.1 从题目描述中 X = [A,B,C,B,D,A,B] , Y[B,D,C,A,B,A] ,目测最大公共子串为 BDAB , BCAB ,最长为4.
2.2 假设从一开始就知道X,Y的最大长度为4 ,那么只要关心X为4的子串与Y进行对比,这样效率就提高了.
2.3 进一步假设X字符串转为char数组后坐标为0,1,2,3,4.....M , 同理Y为0,1,2,3...N
假设 i <= M , j <= N , c[i][j] =LCS( X,Y) . // i ,j 为一个int整数 , c[i][j]为 X的char数组0,1,2,3....i 和Y的char数组0,1,2,3...j 最大公共子串的长度
// LCS 为 longestcommon subsequence ( 最长公共子串 ) 的缩写 .
那么对于X0,1,2,3.....M , Y0,1,2,3....N的最大公共子串长度为
c[i][j] + LCS(X1,Y1)
其中 X1 的坐标 i+1,i+2,.....M ,Y1坐标为j+1,j+2....N.
求最大公共子串长度总结 : 一部分长度( 假设已知) + 另外一部长度( 需要求的 )
四 公式
最大公共子串公式1
if (X[i] == Y[j] ) c[i][j] = c[i-1][j-1] + 1
证明 :
假设X , Y (见图1) , 在X 0,1,2,...i , Y 0,1,2,3...j 中最长公共子串长度为 k ,那么 在X0,1,2,3...,i-1 ,Y0,1,2,3,...,j-1(见图2)中最长公共子串长度为k-1
图1

图2

反证法 : X0,1,2,3...,i-1 ,Y0,1,2,3,...,j-1中最长公共子串长度为k-1不成立, 即存在一个w ( w > k-1 ) ,那么 如上图2 , 当 X[i] == Y[j] 时候, 即在X 0,1,2,...i , Y 0,1,2,3...j 中, 最大公共子串长度为 w+1 > ( k-1 ) +1 > k ,这与原命题矛盾,所以不存在这样一个w值.
即 if (X[i] == Y[j] ) c[i][j] = c[i-1][j-1] + 1
最大公共子串公式2
if (X[i] != Y[j] ) c[i][j] = max( c[i][j-1] , c[i-1][j] ) // max (a ,b) 返回a,b两个数中最大的一个 ,如果相等,则返回a
理解 : c[i][j] 对应图3 , c[i-1][j] 对应图4, c[i][j-1]对应图5, 那么最大公共子串长度一定是c[i-1][j] 和c[i][j-1]中的一个 ,用上面反证法即可证明.
图3
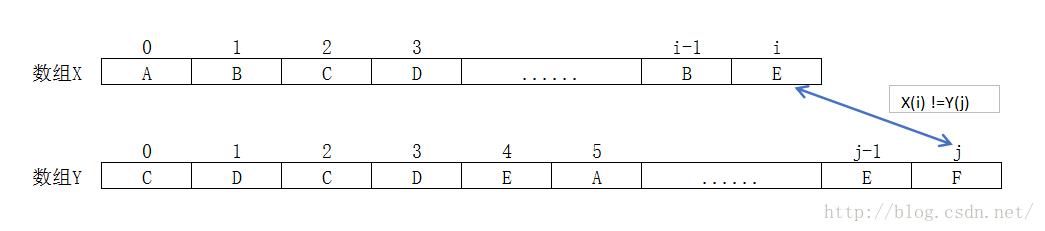
图4

图5
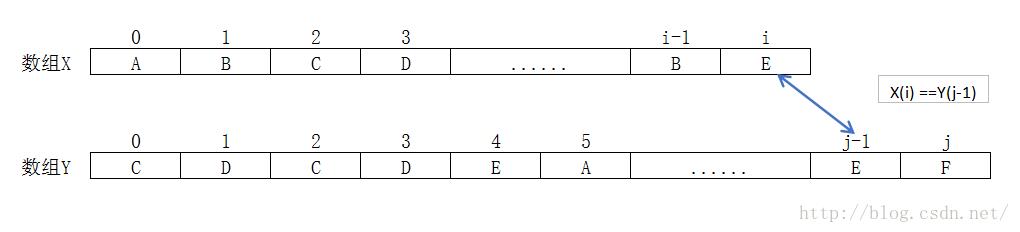
五 递归调用图
假设X0,1,2,3..M,Y0,1,2,3,...N 中M =7 , N = 6,那么它的调用图如下.
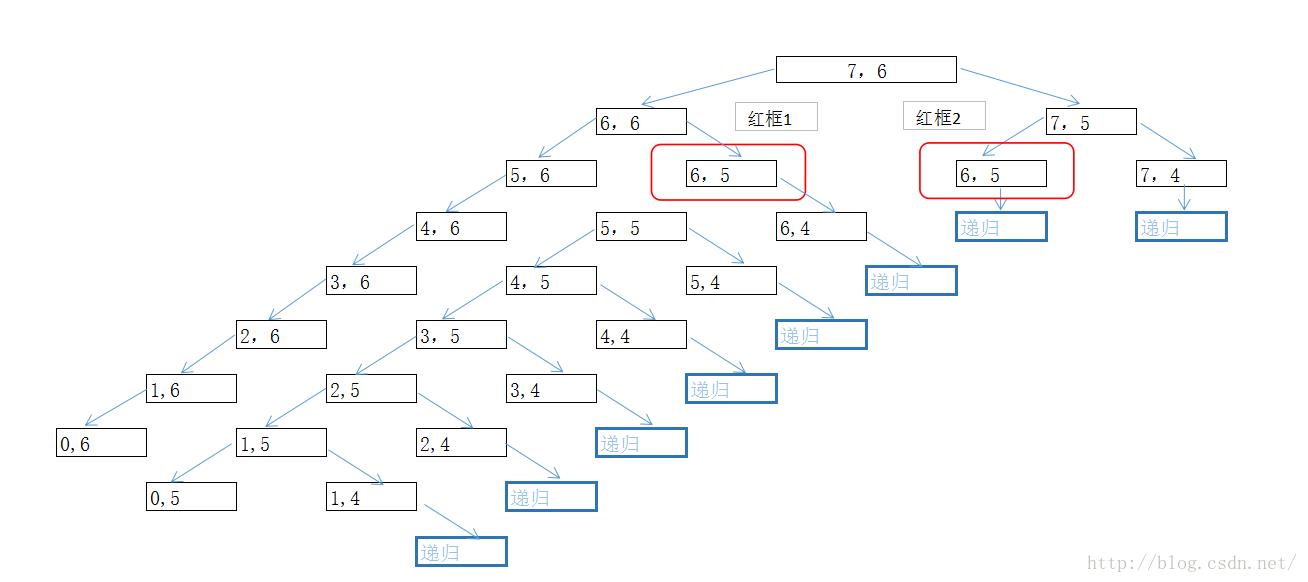
从这幅图中看出
1 树的高度为 M+N = 7+6 = 15
2 时间复杂度 2^(M+N) = 2^13 (比暴力破解时间N*2^M=6*2^7还要多很多, 假设不采用备忘录法和没有重复情况下, 动态规划时间复杂度比暴力破解复杂度高很多,但 经测试在M=29,N=28,时候 ,暴力破解法时间为 300万次 ,动态规划调用1000多次,后面有代码,可自行测试)
3 有少量重复调用,比如红框1和红框2,都是递归6,5这种情况
六 动态规划的特征
1 最优子结构 (包含问题最优解),如 最大公共子串公式2 .
2 重复子问题,如 五 递归调用图
七 自顶向下+备忘录法 java代码
伪代码
LCS(x,y,i,j)
if(x[i]==y[j]) c[i][j] = LCS(x,y,i-1,j-1)+1
else c[i][j] = max(LCS(x,y,i-1,j) , LCS(x,y,i,j-1))
return c[i][j]java代码
LCS.java
public class LCS
private static int[][] c;
private static int counter;
/**
* 判断是否为空
* */
private static boolean isNullOrBlank(String source)
if(source==null||"".equals(source.replace(" ", ""))) return true;
return false;
/**
* 得到最长公共子串
* */
public static int getLcs(String xStr,String yStr)
if( isNullOrBlank(xStr) || isNullOrBlank(yStr) ) return 0;
char[] xChar = xStr.toCharArray();
char[] yChar = yStr.toCharArray();
c = new int[xChar.length][yChar.length];
int lcsMaxNumber = getLcsMaxNumber(xChar,yChar,xChar.length-1,yChar.length-1);
return lcsMaxNumber;
private static int max(int x,int y)
if(x>y) return x;
return y;
// /**
// * 不采用备忘录法
// * 得到LCS最长公共子串的长度
// * */
// private static int getLcsMaxNumber(char[] x,char[] y,int i,int j)
// counter++;
// if(i>=0&&j>=0) // c[i][j]初始化为0,当不为0时,表示已经遍历过
// if(x[i]==y[j])
// c[i][j] = getLcsMaxNumber(x,y,i-1,j-1) + 1;
// else
// c[i][j] = max(getLcsMaxNumber(x,y,i-1,j),getLcsMaxNumber(x,y,i,j-1));
//
// System.out.println("counter = "+counter+" c["+i+"]["+j+"] = " + c[i][j]);
// return c[i][j];
//
//
// return 0;
//
/**
* 备忘录法
* 得到LCS最长公共子串的长度
* */
private static int getLcsMaxNumber(char[] x,char[] y,int i,int j)
counter++;
if(i>=0&&j>=0)
if(c[i][j]==0)
if(x[i]==y[j]) // c[i][j]初始化为0,当不为0时,表示已经遍历过
c[i][j] = getLcsMaxNumber(x,y,i-1,j-1) + 1;
else
c[i][j] = max(getLcsMaxNumber(x,y,i-1,j),getLcsMaxNumber(x,y,i,j-1));
System.out.println("counter = "+counter+" c["+i+"]["+j+"] = " + c[i][j]);
return c[i][j];
return 0;
public static void main(String[] args)
// String x = "ABCBDAB";
// String y = "BDCABA";
String x = "ACCGGTCGAGTGCGCGGAAGCCGGCCGAA";
String y = "GTCGTTCGGAATGCCGTTGCTCTGTAAA";
int number = LCS.getLcs(x, y);
System.out.println(number);
回溯法原理
假设 X = "ABCBDAB"; Y= "BDCABA",它们生成一副下面的图

↖ ↑ ←符号解释
↖ 输出该yj的值,并且向左斜角走一步 ↑ 表示向上走一步 ←向左走一步
那么当 i = 7 , j = 6时候, 输出元素为 ABCB ,把该字符串反向后,为BCBA( BCBA即为X和Y的最大公共子串 )
最大公共完整java代码 (代码中 b+c 为对应上面回溯原理中的图)
public class LCS2
private static int[][] c; //保存长度
private static char[][] b; //保存特殊符号 ↖ ↑ ←
/**
* 判断是否为空
* */
private static boolean isNullOrBlank(String source)
if(source==null||"".equals(source.replace(" ", ""))) return true;
return false;
/**
* 得到最长公共子串
* */
public static String getLCS(String x,String y)
//判断x,y是否为空
if( isNullOrBlank(x) || isNullOrBlank(y) ) return null;
//初始化变量
int m = x.length();
int n = y.length();
b = new char[m][n];
c = new int[m][n];
char[] xChar = x.toCharArray();
char[] yChar = y.toCharArray();
//调用获取最大公共子串长度方法
getLcsMaxNumber(xChar,yChar,xChar.length-1,yChar.length-1);
//回溯法得到最长公共子串
StringBuffer sb = new StringBuffer();
PRINT_LCS(sb,xChar,yChar,m-1,n-1);
return sb.toString();
private static int max(int x,int y)
if(x>y) return x;
return y;
/**
* 备忘录法
* 得到LCS最长公共子串的长度
* */
private static int getLcsMaxNumber(char[] x,char[] y,int i,int j)
if(i>=0&&j>=0)
if(c[i][j]==0)
if(x[i]==y[j]) // c[i][j]初始化为0,当不为0时,表示已经遍历过
c[i][j] = getLcsMaxNumber(x,y,i-1,j-1) + 1;
b[i][j] = '↖';
else
int i_1 = getLcsMaxNumber(x,y,i-1,j);
int j_1 = getLcsMaxNumber(x,y,i,j-1);
if(i_1>j_1)
c[i][j] = i_1;
b[i][j] = '↑';
else
c[i][j] = j_1;
b[i][j] = '←';
return c[i][j];
return 0;
//回溯法得到最长公共子串
private static void PRINT_LCS(StringBuffer sb,char[] x,char[] y,int i,int j)
if(i==0 || j==0 )
if(b[i][j]=='↖')
sb.append(x[i]);
return ;
if(b[i][j]=='↖')
PRINT_LCS(sb,x,y,i-1,j-1);
sb.append(x[i]);
else if(b[i][j]=='↑')
PRINT_LCS(sb,x,y,i-1,j);
else if(b[i][j]=='←')
PRINT_LCS(sb,x,y,i,j-1);
public static void main(String[] args)
// String x = "ABCBDAB";
// String y = "BDCABA";
String x = "ACCGGTCGAGTGCGCGGAAGCCGGCCGAA";
String y = "GTCGTTCGGAATGCCGTTGCTCTGTAAA";
String lcs = LCS2.getLCS(x, y);
System.out.println("最大公共子串为 = " + lcs);
以上是关于动态规划之最长公共子串的主要内容,如果未能解决你的问题,请参考以下文章