Matplotlib 可视化进阶之 PCA 主成分分布图
Posted AI科技大本营
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Matplotlib 可视化进阶之 PCA 主成分分布图相关的知识,希望对你有一定的参考价值。

作者 | 云朵君
来源 | 数据STUDIO
这乍是一个简单的散点图,有两个主轴,显示一些高斯数据。并且在图中添加了一个垂直于第一个主成分轴的直方图,以显示主成份轴上的分布。这个图可能看起来很简单(散点图和有方向的直方图),其实不然,绘制这样的图也比较困难。主要的困难是要使直方图处于正确的位置、大小和方向,位置必须在数据坐标中设置,大小必须在图形标准化坐标中给出,方向必须在角度中给出。更复杂的是,我们想要用数据点来表示直方图上方柱子及文本的高度。

首先导入需要的模块
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
from matplotlib.transforms import Affine2D
import mpl_toolkits.axisartist.floating_axes as floating_axes
# 设置随机数种子
np.random.seed(123)数据准备
生成一些数据。
#
Z0 = np.random.normal(0, (1.25, 0.75), (150, 2))
# Z0: 2D的随机array点
Z1 = Affine2D().rotate_deg(35).transform(Z0)
# Z1: 旋转后的Z0
Zm = Z1.mean(axis=0)
# Z1的均值:Zm = np.array([ 0.13746892, -0.02793329])PCA 主成分分析
注意,对于某些点,PC1和PC2需要转置。
W, V = np.linalg.eig(np.cov(Z1.T))
# W: 特征值, V: 特征向量
PC1, PC2 = V[np.argsort(abs(W))]
# PC1, PC2: 第一和第二主成分
if PC2[1] < 0:
# 确保 PC2 "向上"
PC2 = -PC2
rotation = 180 * np.arctan2(*PC1) / np.pi
# 37.89555000213858
T = np.array([PC1[0], PC1[1]])
# PC1 切向量
O = np.array([PC2[0], PC2[1]])
# PC1正交向量PC1
array([0.61422391, 0.78913179])
PC2
array([-0.78913179, 0.61422391])绘制散点图
设置画布
fig = plt.figure(figsize=(8, 8))
ax1 = fig.add_axes([0.05, 0.05, 0.9, 0.9], aspect=1)绘制散点图
绘制散点图,并设置轴参数。
ax1.scatter(Z1[:, 0], Z1[:, 1],
s=50, fc="C0",
ec="white", lw=0.75)
ax1.set_xlim([-3, 6])
ax1.set_xticks([-3, 6])
ax1.set_xticklabels([])
ax1.set_ylim([-3, 6])
ax1.set_yticks([-3, 6])
ax1.set_yticklabels([])
ax1.spines["top"].set_visible(False)
ax1.spines["right"].set_visible(False)
fig.add_axes()为图形添加轴。
add_axes()方法需要一个由4个元素组成的list对象,分别对应图形的左、底、宽、高。每个数字必须在0和1之间。
2D的随机生成的array点:
Z0 = np.random.normal(0, (1.25, 0.75), (150, 2))Z1是旋转后的Z0:
Z1 = Affine2D().rotate_deg(35).transform(Z0)绘制 PCA 轴
P0: 沿着PC1的长线的端点
P0 = np.vstack([Zm - T * 10, Zm + T * 10])
ax1.plot(P0[:, 0], P0[:, 1],
color="black", linestyle="--",
linewidth=0.75, zorder=10)array([[-6.0047702 , -7.91925121],
[ 6.27970805, 7.86338463]])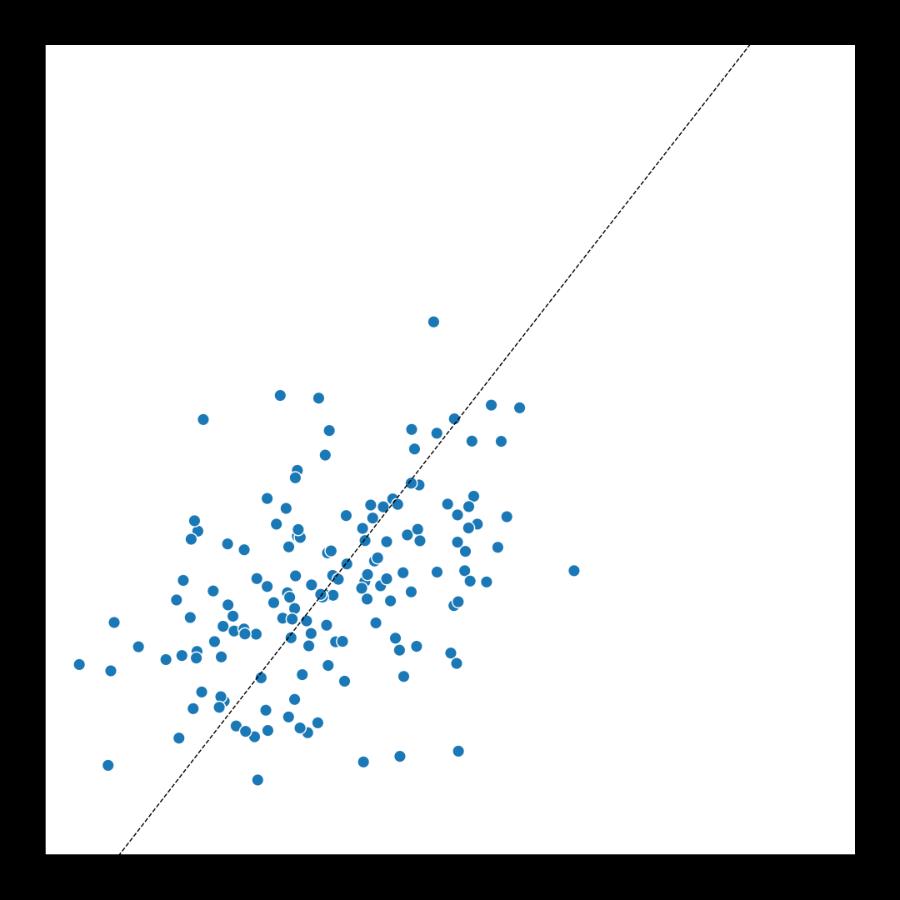
计算沿正交方向到主成分分析分布的宽度。主轴是通过旋转点并在Y轴上取max来实现的。
transform = Affine2D().rotate_deg(-rotation)
P1 = transform.transform(Z1 - Z1.mean(axis=0))
# P1 : 沿着x轴,旋转Z1
# print(P1)
d = np.abs(P1[:, 1]).max()
# d : P0 到 Z1 之间的最大距离
# 画一个矩形,围绕分布和朝向主成分分析主轴
# P2: 矩形周围Z1
P2 = np.vstack(
[ Zm - 10 * T - d * O,
Zm + (6 - d) * T - d * O,
Zm + (6 - d) * T + d * O,
Zm - 10 * T + d * O,
])
ax1.add_patch(
Polygon( P2,
closed=True, fill=True,
edgecolor="None", facecolor="C0",
alpha=0.1, zorder=-50, ))绘制矩形边框
# P3, P4 : edges of P2 parallel to PC1
P3 = np.vstack([Zm - 10 * T, Zm + (6 - d) * T]) - d * O
plt.plot(P3[:, 0], P3[:, 1],
color="C0", linestyle="-",
linewidth=0.75, alpha=0.25)
P4 = np.vstack([Zm - 10 * T, Zm + (6 - d) * T]) + d * O
plt.plot(P4[:, 0], P4[:, 1],
color="C0", linestyle="-",
linewidth=0.75, alpha=0.25)
ax1.scatter(Zm[0], -2.85, s=50,
color="black", marker="v",
clip_on=False)
ax1.scatter(-2.85, Zm[1], s=50,
color="black", marker="<",
clip_on=False)
offset = 30
x, y = -1.2, 2
bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
arrowstyle = "->",
connectionstyle = "angle,angleA=0,angleB=90,rad=10")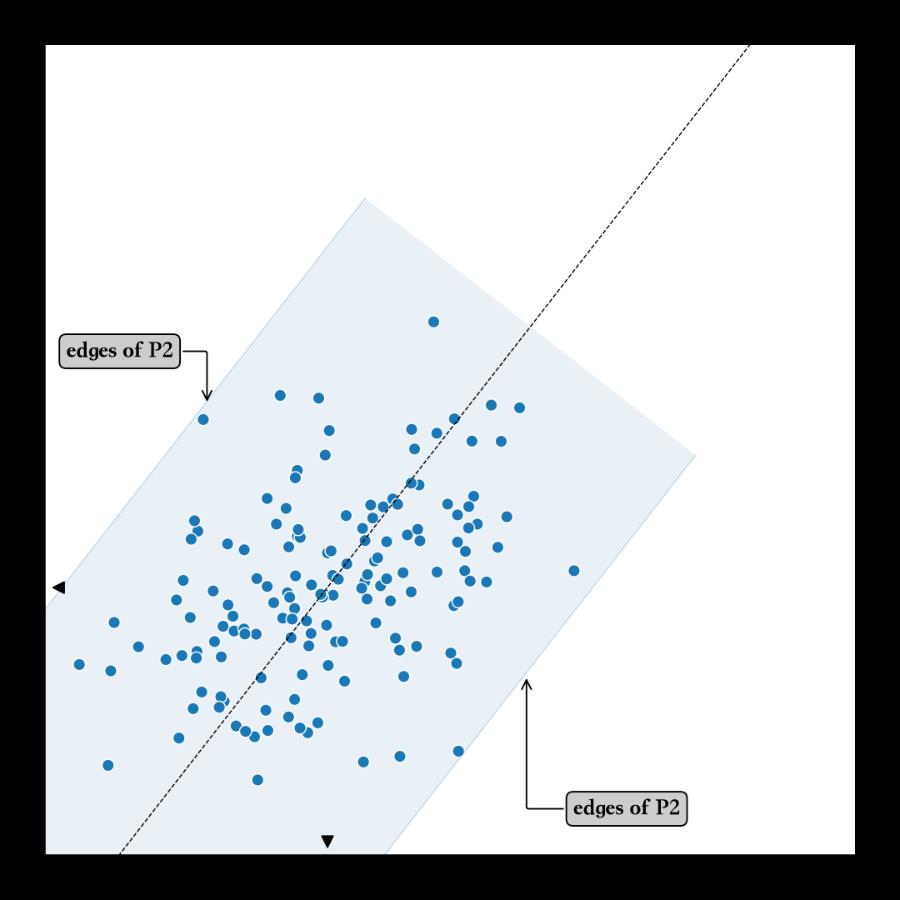
定位和平移副轴
这一步是相对复杂些,下面我们拆分多个步骤演示绘制过程。
计算直方图的中心
沿着PC1,并且离矩形稍微远一点。
C = Zm + 6 * T计算坐标和大小
该步骤是在标准化Figure坐标中计算坐标和大小。
x, y = fig.transFigure.inverted().transform(
ax1.transData.transform(C))
xo, yo = fig.transFigure.inverted().transform(
ax1.transData.transform(C + 2 * d * O))
h0 = w0 = np.sqrt((xo - x) ** 2 + (yo - y) ** 2)直方图轴的准备
创建副轴,它必须是方轴: xmax-xmin = ymax-ymin。也可以是非方轴,但它会使问题复杂化。
xmin, xmax = -16, 16
# 对于直方图来说,对称xlim需要"足够大"
ymin, ymax = 0, xmax - xmin
# Y的范围,与x具有同样的范围,且正的
transform = Affine2D().rotate_deg(-rotation)
helper = floating_axes.GridHelperCurveLinear(
transform, (xmin, xmax, ymin, ymax))
ax2 = floating_axes.FloatingSubplot(
fig, 111, grid_helper=helper, zorder=0)绘制旋转轴
现在已经明确了轴的大小,而它是旋转的。
当我们指定大小和位置时,它与非旋转轴相关,因此我们需要计算边界框。为此,我们旋转四个坐标,从中推导出边界盒坐标。
transform = Affine2D().rotate_deg(-rotation)
# 柱状图的轮廓
R = transform.transform(
[ (x - w0 / 2, y - h0 / 2),
(x + w0 / 2, y - h0 / 2),
(x - w0 / 2, y + h0 / 2),
(x + w0 / 2, y + h0 / 2),
])
# 直方图轴的宽度
w1 = R[:, 0].max() - R[:, 0].min()
# 直方图轴的高度
h1 = R[:, 1].max() - R[:, 1].min()
ax2.set_position((x - w1 / 2, y - h1 / 2, w1, h1))
# 添加柱状图轴
fig.add_subplot(ax2)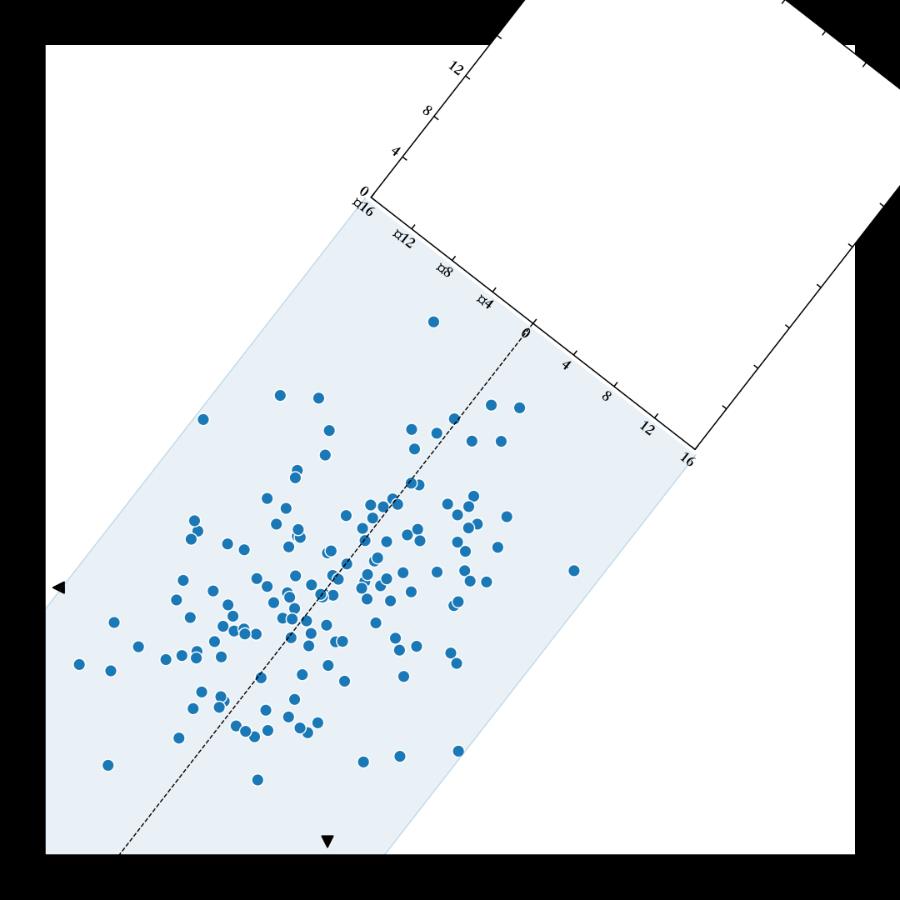
装饰轴线
只显示底部轴,并且设置底部轴标签不可见,刻度线朝外。
ax2.axis["left"].major_ticklabels.set_visible(False)
ax2.axis["bottom"].major_ticklabels.set_visible(False)
ax2.axis["bottom"].major_ticks.set_tick_out(True)
ax2.axis["left"].set_visible(False)
ax2.axis["right"].set_visible(False)
ax2.axis["top"].set_visible(False)
ax2.set_xticks([0, 1])
ax2.patch.set_visible(False)显示直方图
这里需要注意X轴的范围。
X0: 归一化的
bins范围[0,1]
X1: 拉伸箱子范围[xmin, xmax] = [-16, 16]
counts, bins = np.histogram(-Z1 @ PC1, bins=12)
# 垂直于PC1方向的-Z1直方图,有12个箱子
X0 = (bins - bins[0]) / (bins[-1] - bins[0])
X1 = xmin + (xmax - xmin) * X0
Y = np.array(counts)
# 这个辅助轴对于画东西是必要的(不知道为什么)
ax2_aux = ax2.get_aux_axes(transform)
# 绘制直方图
ax2_aux.hist(X1[:-1], X1,
weights=Y, facecolor="C0",
edgecolor="white", linewidth=0.25)np.histogram()是一个生成直方图的函数。
histogram(a, bins=10, range=None,
weights=None, density=False)a是待统计数据的数组bins指定统计的区间个数range是一个长度为2的元组,表示统计范围的最小值和最大值,默认值None,表示范围由数据的范围决定weights为数组的每个元素指定了权值,histogram()会对区间中数组所对应的权值进行求和density为True时,返回每个区间的概率密度;为False,返回每个区间中元素的个数
>>> PC1
array([0.61422391, 0.78913179])
>>> Z1
array([[-1.54066105, -0.16563199],
[ 0.93773438, -0.72252605],
[-1.30287079, 0.59974387],
[-2.30026345, -2.00336603],
[ 1.66909925, 0.37514488],
...])
# Z1.shape = (150, 2)
>>> counts, bins = np.histogram(-Z1 @ PC1, bins=12)
>>> counts
array([ 3, 4, 9, 19, 16, 24, 24, 18, 15, 13, 4, 1])
>>> bins
array([-3.11782694, -2.60852498, -2.09922301,
-1.58992105, -1.08061908, -0.57131712,
-0.06201515, 0.44728681, 0.95658878,
1.46589075, 1.97519271, 2.48449468,
2.99379664])添加标签
这里添加文本注意旋转参数:rotation
dx, dy = (X1[1] - X1[0]) / 2, 0.75
for x, y in zip(X1, Y):
ax2_aux.text(
x + dx,
y + dy, "%d" % y,
ha="center", va="center",
size=8, rotation=-rotation,)
参考资料
[1]
https://matplotlib.org/stable/api/_as_gen/mpl_toolkits.axisartist.grid_helper_curvelinear.GridHelperCurveLinear.html
[2]Scientific Visualisation-Python & Matplotlib


往期回顾
分享
点收藏
点点赞
点在看以上是关于Matplotlib 可视化进阶之 PCA 主成分分布图的主要内容,如果未能解决你的问题,请参考以下文章
R语言进行主成分分析(PCA)使用prcomp函数进行主成分分析:碎石图可视化(scree plot)R通过线图(line plot)来可视化主成分分析的碎石图(scree plot)
R语言plotly可视化:使用PCA算法进行数据降维使用plotly可视化PCA所有的主成分绘制散点图矩阵降维后的两个(三个)核心主成分的二维三维可视化图形方差解释的量载荷图等
R语言进行主成分分析(PCA)使用prcomp函数进行主成分分析:碎石图可视化(scree plot)R通过条形图(bar plot)来可视化主成分分析的碎石图(scree plot)