区块链与密码学第10-6讲：身份鉴别协议

Posted 2022-05-30 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

10-6身份鉴别协议

在一个安全的身份认证协议中，要保证用户身份识别的安全性，身份鉴别协议至少要满足以下条件：

证明者P能够向验证者V证明他的确是P（P向V证明自己有P的私钥）。

在证明者P向验证者V证明他的身份后，验证者V没有获得任何有用的信息（V不能模仿P向第三方证明他是P）。

该协议的目的是证明者P向验证者V证明他的身份（私钥），且事后V不能冒充P。

| Feige-Fiat-Shamir 零知识身份鉴别协议

1986年，Feige、Fiat和Shamir基于零知识的思想设计了一个零知识身份鉴别协议，这就是著名的Feige-Fiat-Shamir零知识身份鉴别协议。

该协议的目的是证明者P向验证者V证明他的身份（私钥），且事后V不能冒充P。

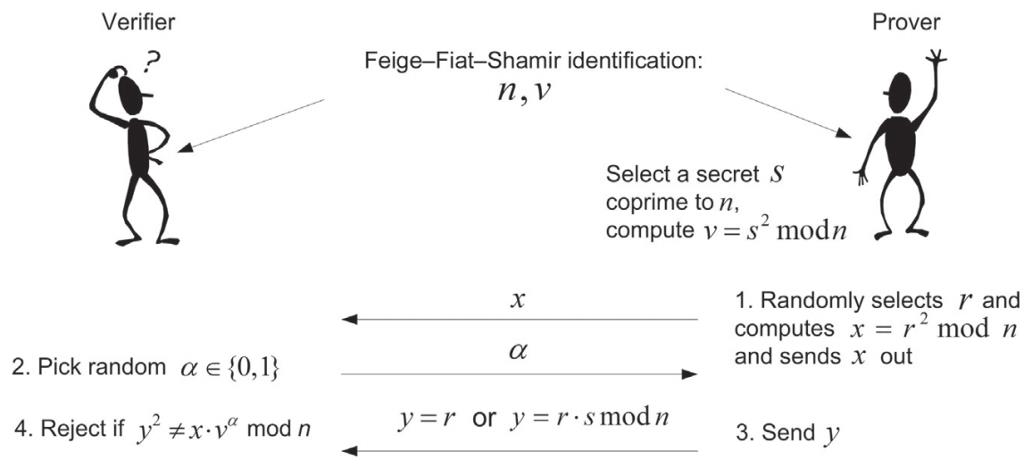
简化版本

系统初始化（一次性）：

信任中心TA选择并公布一个RSA型模数n=p⋅q，并对素数p和q保密。 

每一个参与者P选择一个与n互素的秘密值s，1≤s≤n-1，并计算v=(\\mod n)，并向TA注册v为其公钥。

鉴别协议流程：

1. P选择一个随机数r，1≤r≤n-1，计算并发送x=(mod n)给V。

2. V随机选择一个比特值，并将α发送给证明者。

3. P根据α做出不同的响应：若α=0，令y=r；若α=1，令y=r⋅s (mod n)。

4. V验证等式=x⋅(mod n)。如果等式不成立或者y=0，V不接受证明。否则，进行下一轮证明。验证者V执行上述证明过程t轮后，且均未拒绝，则验证者接受证明者P的证明，即相信他的身份。

简化版本的性质分析

完备性：如果证明者知道秘密值s，他对于不同的α都可以做出正确的响应。显然，诚实验证者接收的概率为1。

可靠性：如果证明者不知道秘密值s ，那么他只能够以1/2的概率欺骗验证者。执行t轮后，欺骗概率下降到。

零知识性：协议交互过程中泄露的信息有：x=(mod n)、y=r或y=r⋅s(mod n)，即(x,y)。模拟器的模拟方式：随机选择y，并令x=（当α=0）或x=/v（当α=1）。模拟器产生的(x,y)与真实交互的(x,y)是计算不可区分的。

完整版本

系统初始化（一次性）：

1. 信任中心TA选择并公布一个RSA型模数n=p⋅q，并对素数p和q保密。 

2. 每一个参与者P选择k个与n互素的秘密值,,⋯,，1≤≤n-1，并计算=(\\mod n)，并向TA注册(,,⋯,)为其公钥。

鉴别协议流程：

1. P选择一个随机数r，1≤r≤n-1，计算并发送x=(mod n)给V。

2. V随机选择k个比特值=(,,⋯,)，并将发送给P。

3. P计算y=(mod n)，并将y发送给V。

4. V验证等式=(mod n)。如果等式不成立或者y=0，V不接受证明。否则，进行下一轮证明。

验证者V执行上述证明过程t轮后，且均未拒绝，则验证者接受证明者P的证明，即相信他的身份。

完整版本的性质分析

完备性：显然，诚实验证者接收的概率为1。

可靠性：如果证明者不知道秘密值s ，那么他只能够以1/的概率欺骗验证者。执行t轮后，欺骗概率下降到。

零知识性：同样地，与简化版本一致，交互数据元组(x,y)可以被模拟器模拟，达到计算不可区分性。

安全假设

无论简化版本还是完整版本，协议的安全性依赖于未知分解的大合数的模平方根求解难题。这个问题等价于大合数的分解困难问题。

参数选择

以完整版本为例，k⋅t（简化版本中k=1）需要足够大，才能够保证非诚实证明者欺骗成功概率几乎可忽略。同时，n的分解困难性也是安全性考虑之一。

安全平衡

每增加一轮协议，计算量和通信量均上升，但安全性越高。因此，需要在保证足够安全的前提下，减少协议重复轮数t，提升效率。

今天的课程就到这里啦，下节课我们将继续学习身份鉴别协议，敬请期待！

同学们可以关注点宽学园，每周持续更新区块链系列课程，小宽带你进入区块链世界。我们下节课见啦。

【区块链与密码学】课堂回顾：

区块链与密码学系列文章合集