SS2022-Z变换-性质-什么是z变换的时移特性?
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SS2022-Z变换-性质-什么是z变换的时移特性?相关的知识,希望对你有一定的参考价值。
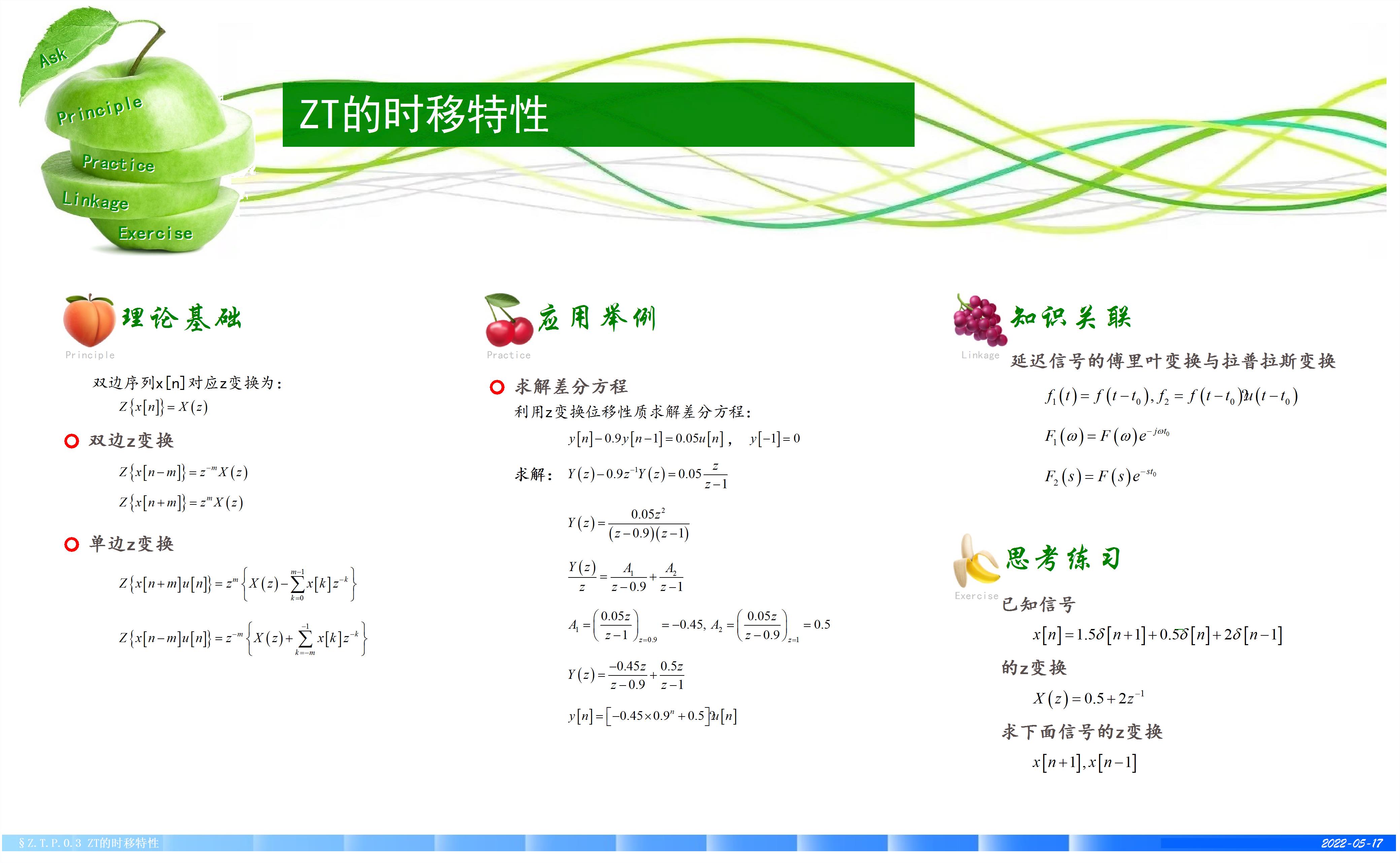
简 介: 本文介绍了z变换时移特性。
关键词: z变换,时移特性
Z变换性质-时移特性
§01 理论基础
z变换的时移特性表示了序列在时间轴上 右移(延迟)或者左移(超前)后的在变换与 原序列z变换之间的关系。 这种关系随着z变换采用双边z变换 还是单边z变换而有所区别。 下面先考虑双边z变换。
1.1 双边z变换
如果序列 x [ n ] x\\left[ n \\right] x[n] 的双边z变换为 Z x [ n ] = X ( z ) Z\\left\\ x\\left[ n \\right] \\right\\ = X\\left( z \\right) Zx[n]=X(z) 那么,序列左移 x [ n + m ] x\\left[ n + m \\right] x[n+m] 和右移 x [ n − m ] x\\left[ n - m \\right] x[n−m] 对应的 z 变换为 Z x [ n − m ] = z − m X ( z ) Z\\left\\ x\\left[ n - m \\right] \\right\\ = z^ - m X\\left( z \\right) Zx[n−m]=z−mX(z) Z x [ n + m ] = z m X ( z ) Z\\left\\ x\\left[ n + m \\right] \\right\\ = z^m X\\left( z \\right) Zx[n+m]=zmX(z)其中 m 为任意正整数,表示位移长度。 平移后序列z变换收敛域不发生变化。
双边z变换时移特性比较简单, 序列右移m位, 对应的z变换前面多出一个 z的-m 次方因子; 序列左移m位, z 变换前面乘以一个 z 的 m 次方因子。 由于平移不会改变序列在 n 趋向于 正无穷和负无穷的变化趋势, 所以对应的收敛域也不会发生变化。
1.1.1 位移特性证明
利用变量替换方法,可以方便证明位移特性:
Z x [ n − m ] = ∑ n = − ∞ + ∞ x [ n − m ] z − n Z\\left\\ x\\left[ n - m \\right] \\right\\ = \\sum\\limits_n = - \\infty ^ + \\infty x\\left[ n - m \\right]z^ - n Zx[n−m]=n=−∞∑+∞x[n−m]z−n = z − m ∑ k = − ∞ + ∞ x [ k ] z − k = z − m X ( z ) = z^ - m \\sum\\limits_k = - \\infty ^ + \\infty x\\left[ k \\right]z^ - k = z^ - m X\\left( z \\right) =z−mk=−∞∑+∞x[k]z−k=z−mX(z)
下面给出z变换时移特性的简单证明。 直接利用z变换公示, 将其中的变量n-m设为k。 那么n等于k+m, 将z的(-n)次方中的n替换为k+m, m是常量提到最前面。 k是累加中的变量。 这是对x[n]的z变换。 把X(z)合并前面的指数项, 就得到时移后的序列z变换。
1.2 单边z变换
对于双边序列 x [ n ] x\\left[ n \\right] x[n] ,它的单边 z 变换为 Z x [ n ] u [ n ] = X ( z ) Z\\left\\ x\\left[ n \\right]u\\left[ n \\right] \\right\\ = X\\left( z \\right) Zx[n]u[n]=X(z) 则序列左移、右移对应的 z 变换为 Z x [ n + m ] u [ n ] = z m X ( z ) − ∑ k = 0 m − 1 x [ k ] z − k Z\\left\\ x\\left[ n + m \\right]u\\left[ n \\right] \\right\\ = z^m \\left\\ X\\left( z \\right) - \\sum\\limits_k = 0^m - 1 x\\left[ k \\right]z^ - k \\right\\ Zx[n+m]u[n]=zmX(z)−k=0∑m−1x[k]z−k Z x [ n − m ] u [ n ] = z − m X ( z ) + ∑ k = − m − 1 x [ k ] z − k Z\\left\\ x\\left[ n - m \\right]u\\left[ n \\right] \\right\\ = z^ - m \\left\\ X\\left( z \\right) + \\sum\\limits_k = - m^ - 1 x\\left[ k \\right]z^ - k \\right\\ Zx[n−m]u[n]=z−mX(z)+k=−m∑−1x[k]z−k
对于单边 z 变换, 时移特性略显麻烦。 对于左移来讲, 它所对应的 z 变换除了原有的 X(z) 乘以指数项之外, 还需要减去这部分内容, 它们是原来序列从 0 到 m-1 对应的序列的 z 变换。 对于右移, 则是在原有 X(z) 乘以指数项之外, 加上原来从 -m 到 -1 对应序列的 z 变换。
这一点从序列的图形上可以看得更清楚。 上面是左移对应序列的波形, 在单边 z 变换下, n=0 之后的前面 m 个数据移出了变换累加范围; 下面是右移对应序列的波形, 单边 z 变换下, n 小于 0 前面的 m 个数据移入变换累加的范围。
考虑到上述数据移入移出的过程, 使用同样的变量替换方法可以证明单边 z 变换公示。 这里就不在重复了。
§02 应用举例
2.1 求解差分方程
已知差分方程 y [ n ] − 0.9 y [ n − 1 ] = 0.05 u [ n ] y\\left[ n \\right] - 0.9y\\left[ n - 1 \\right] = 0.05u\\left[ n \\right] y[n]−0.9y[n−1]=0.05u[n] 边界条件 y [ − 1 ] = 0 y\\left[ - 1 \\right] = 0 y[−1]=0 ,利用 z 变换时移性质求解改差分方程。
◎ 求解:
对方程两端分别取 z 变换, 利用单边 z 变换性质
Y
(
z
)
−
0.9
z
−
1
Y
(
z
)
=
0.05
z
z
−
1
Y\\left( z \\right) - 0.9z^ - 1 Y\\left( z \\right) = 0.05z \\over z - 1
Y(z)−0.9z−
