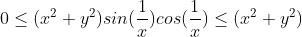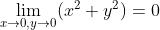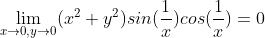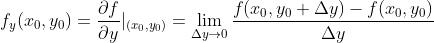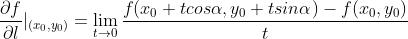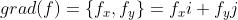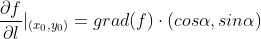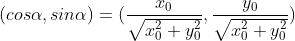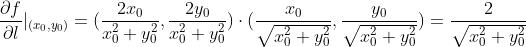数学知识整理:函数 & 梯度
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学知识整理:函数 & 梯度相关的知识,希望对你有一定的参考价值。
1 函数的基本概念
1.1 函数的定义

| A | B | f |
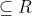 | 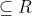 | 一元函数 |
 | 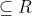 | n元函数 |
 |  | n元m维向量函数 |
1.2 内点,外点和边界点
给定集合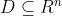 ,对
,对 ,如果满足”条件“,那么p是:
,如果满足”条件“,那么p是:
| 条件 | p的分类 |
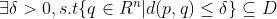 | D的内点 |
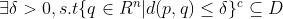 (c表示补集) (c表示补集) | D的外点 |
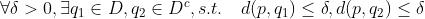 | D的边界点 |
1.2.1 性质
- P是D的内点<——>P是
 的外点
的外点 - P是D的边界点<——>任意以P为圆心的圆盘既有D的内点也有D的外点
1.3 函数的连续性

1.3.1 闭区间上的多元连续函数的基本性质
- 有界性
- 介值定理
- 设函数f(x)在闭区间[a,b]上连续,并且f(a)≠f(b),那么一定存在一个
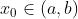 ,使得
,使得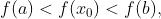 或者
或者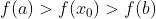
- 设函数f(x)在闭区间[a,b]上连续,并且f(a)≠f(b),那么一定存在一个
- 最值定理
- 设函数f(x)在闭区间[a,b]上连续,则函数f(x)在闭区间[a,b]上就一定存在最大值和最小值。
- 零点定理
- 设函数f(x)在闭区间[a,b]上连续,并且f(a)f(b)<0,那么至少存在一个
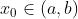 ,使得
,使得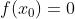
- 设函数f(x)在闭区间[a,b]上连续,并且f(a)f(b)<0,那么至少存在一个
1.4 夹逼定理

1.4.1 举例
而
所以
2 偏微商
如果 存在,那么
存在,那么 在
在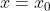 处连续
处连续
如果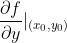 存在,那么
存在,那么 在
在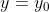 处连续
处连续
4 连续、可导、可微之间的关系
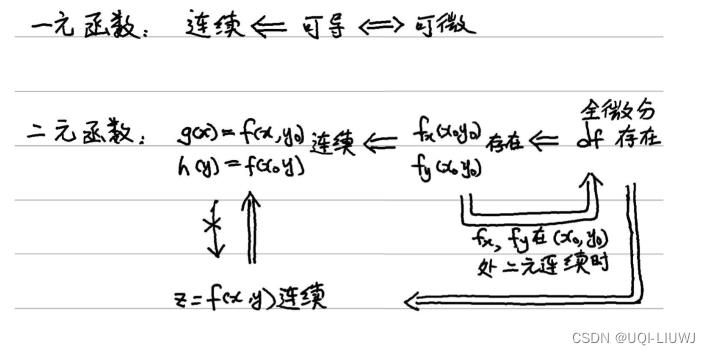
5 梯度
全微分: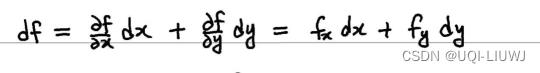
过
处的切平面P:
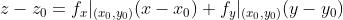
5.1 方向微商
给定直线l,过点
,方向为
,函数f在l方向上的变化率成为方向微商。
记为
如果df存在,那么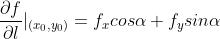
5.1.0 梯度的定义
定义向量
于是
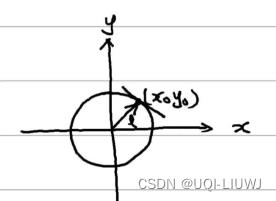
5.1.1 梯度的几何解释
- 梯度的方向是该点处改变最大的方向
- 梯度的模长是该方向的微商的绝对值
- 给定二元可微函数f,以及一个点M,如果grad(f)不是零向量,那么grad(f)和过M点的等高线的切线垂直

5.1.2 举例
求函数
在点
上沿与此点等高线垂直的方向导数
解:
方向向量
所以
5.2梯度的运算规则
u,v是函数,c是常数
- grad(u±v)=grad(u)±grad(v)
- grad(uv)=ugrad(v)+vgrad(u)
- grad(cu)=cgrad(u)
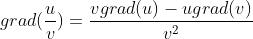

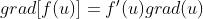
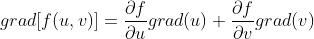
以上是关于数学知识整理:函数 & 梯度的主要内容,如果未能解决你的问题,请参考以下文章