多项式芝士总结

Posted 2022-05-11 Flame♡

欧拉公式：$e^{xi}=cosx+isinx$

当x取π的时候 有

$e^{\pi i}=cos\pi +isin\pi =1$

所以对于$x^n=1$

$x$ 可能的一个解是 $\frac{e^{2\pi i}}{n}$

$w_n=e^{\frac{2\pi i}{n}}$

那么解集是$w_n^k|k\in [0,n)$ (证明考虑欧拉公式） 别忘了是n次方，之所以范围是[0,n) 是因为等于n的时候 可以整体减去2π 答案不变

$w_n^n=1$

有以下性质：

① $w_n^k$是互异的，保证用于插值的个数是对的

② $w_{2n}^{2k}=w_n^k$ (一分两半值不变 可以分治)

③ $w_n^{\frac{n}{2}+k}=-w_n^k$ （直角坐标系上单位圆） （前半可以推后半）

以上都是在fft求点值的过程中用的 最后还需要从点值变回系数

④ $k\ne 0,\sum _{i=0}^{n-1}(w_n^k{)}^i=0$ (感性理解 奇数次数和偶数次数相同)

两个复数相乘，模等于两个模相乘，辅角相加

具体来说 例如两个模是$\sqrt{a^2+b^2}$ $\sqrt{c^2+d^2}$

那么新的模式$\sqrt{a^2+b^2}\times \sqrt{c^2+d^2}$

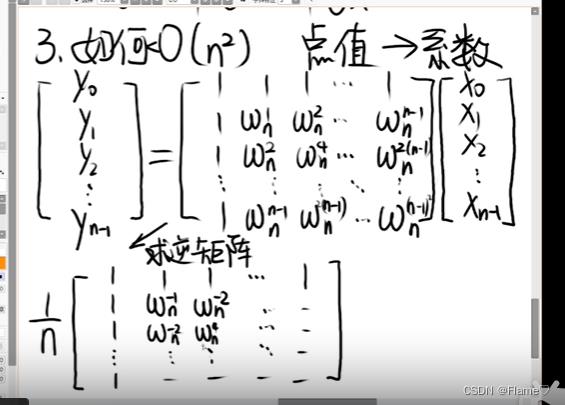
逆矩阵里是取倒数

之所以FFT时 ab数组是对应位置相乘 原因在于 本质上ab相乘对应卷积没有实际含义，只是为了求逆的方便，因此对应位置相乘

写代码的时候之所以写的是$\pi /mid$ 是因为本来应该是$(2\pi )/(2mid)$ 刚好约一下

NTT的时候 则$g_n^k=x^{k(p-1)/n}$,其中 n是长度，k是幂 p是质数，x是p的一个原根

NTT常用质数：998244353,469762049,1004535809 原根都是3