潘周聃之Python分聃 -----数字雨加入潘周聃运动曲线

Posted 2022-05-11 勇敢di牛牛

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了潘周聃之Python分聃 -----数字雨加入潘周聃运动曲线相关的知识，希望对你有一定的参考价值。

😽作者：勇敢di牛牛
🚀个人项目地址：englishlearningapp
个人简介：有一年工作经验的大学生。
工作：汽车系统应用开发（阿里集团）
个人网站：牛牛の小窝
🚏独学而无友，则孤陋而寡闻

前言

相信各位同学最近一定被潘周聃刷屏和洗脑了，互联网上也出现了这种各样的模仿者，做为思维活跃的IT人，网上冲浪先进分子，以及整活小能手，我们当然也不能落伍，话不多说，整活开始。

什么是潘周聃运动曲线

首先，这个在曲线在热点时间出现之前是不存在的，这条曲线是博主勇敢di牛牛在总结了潘周聃的起身动作特点后总结出来的。下面详细介绍曲线产生的过程。

模型求解：

原视频动作分析

【潘中单】潘周聃走路⚡️原版

上面是原版视频，通过对比其他模仿者的视频，我们可以发现此次热点动作的核心在于潘同学起身时，身体重心相对于起始轴的偏移
首先我们对该动作的重心变化做一个简单的分析：这是普通人

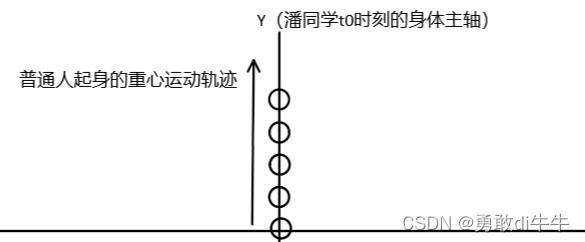
可以看到重心一般情况是垂直上升的，并不会突然产生偏移。
这是潘同学：

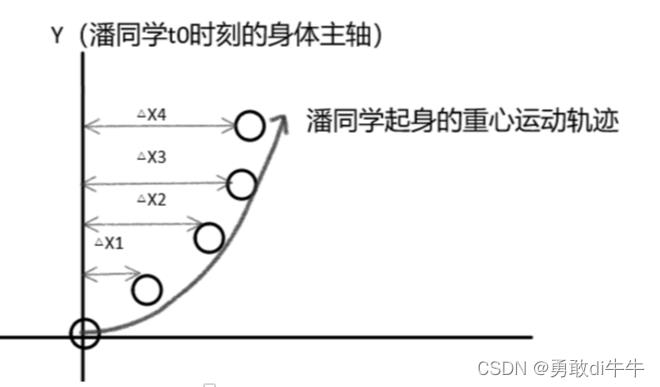
当然，这只是一个粗略的轨迹，真正的轨迹有待进一步拟合，
要想较好的拟合出运动轨迹，我们需要知道两个参数。

相对与主轴的偏移量随时间t的变化：
△x = f(t)
垂直方向的运动分量：
y = f(t)

垂直方向运动模型求解：

首先是比较简单的垂直方向，在初中我们学习过，人在起立的时候是先加速后减速，
设速度为V(t)，则
y = V(t)t
我们暂且先用一个先增后减的函数来模拟速度：

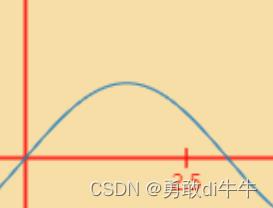
假设：V(t) = sin(t),
这时聪明的你肯定会说，当 t>π 时速度不就小于0了，总不能再坐回去吧？
所以说为了防止它坐回去，我们设起身运动的总时间为T，那么完成起身动作后有：
v = 0且t = T，根据三角函数特性我们很容易得出：
$V(t) = sin(tπT^-1)$
不同的身高H对应不同的时间T，所以这里还需要一个常数：设为β
则有：
$\\int_0^Tβsin(tπT^-1)dt\\,.$
一个很简单的定积分方程，很容易解的：
$β = H π / 4 T$
所以垂直方向的轨迹我们就暂时搞定：
$Hπ/4T\\int_0^tsin(tπT^-1)dt\\,.$
而上面的方程也符合我们生活中的一条现象：
不同身高的人完成起身动作的时间其实是差不多的
因为当y = H/2 时，T与H无关。

水平方向运动模型求解：

动态不好分析，我们先来看一张图片

是不时感觉似曾相识，没错，他和我们的tanX较为相似：

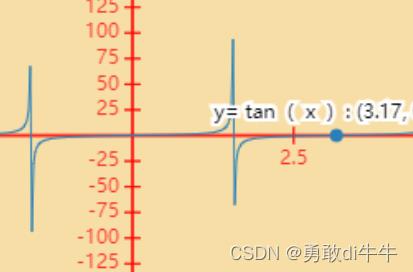
这样还不是很直观，没关系，让我们把他倒过来：

我们肯定也不能直接用这个函数，需要对他做一下变换，取出我们想要的东西，
首先这个函数我们只需要一部分，我们的X是从0开始，所以我们做如下变化：

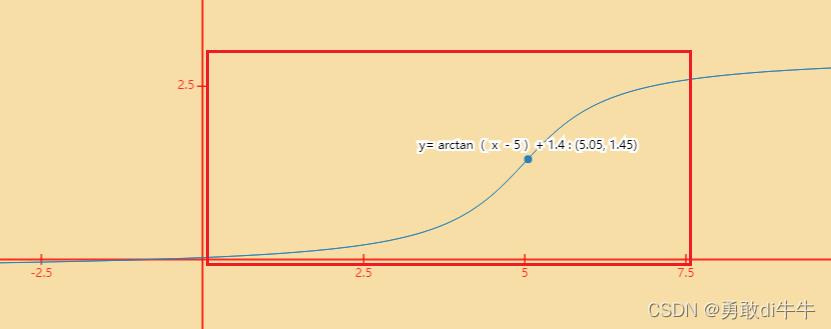
我们取上面的 $\\quad\\forall x\\in\\mathbb [0, 9]$
需要注意：这里的y是随X变化，并不是t
对其求反函数我们算出相对于X轴的偏移速率，即潘同学重心相对于初始身体轴的偏移速率：
得出：
$Δ X = a r c t a n (x - 5) + 1.4$
因为为了方便观察，我们之前去了反函数，这里需要换回去。
对应的： $\\quad\\forall y\\in\\mathbb [0, 9]$
这里的9是我们的模型终点，即我们起身动作重心的垂直偏移量：得到
$y m a x = H / 2$
即： $\\quad\\forall y\\in\\mathbb [0,H/2]$
重心的水平偏移量大概为身高的1/4，函数本身已经满足这个特性，我们这里不再考虑。将此模型取一个单位，考虑到身高后的方程为：
$Δ X = H / 18 a r c t a n (18 y / H - 5) + 1.4$
有细心同学可能会问这里为什么是18，别忘了我们变换最大区间的时候那个9没了，所以要补偿在这里，才能保持形状不变，这里是初二知识了。

模型验证

静态验证

下面我们使用Python的matplotlib库绘图，对轨迹进行一个验证，

import matplotlib.pyplot as plt
import numpy as np


def path(H):
    # H是我们测试模型的身高
    y = np.arange(0.1, H / 2, 0.1)  # y方向区间

    # x = pow((pow(y,2) - 10*y + 26),-1)
    x = H / 18 * (np.arctan(18 * y / H - 5) + 1.4)
    plt.plot(x, y)
    plt.show()


path(180)

path(90)

path(160)

这是180 的你

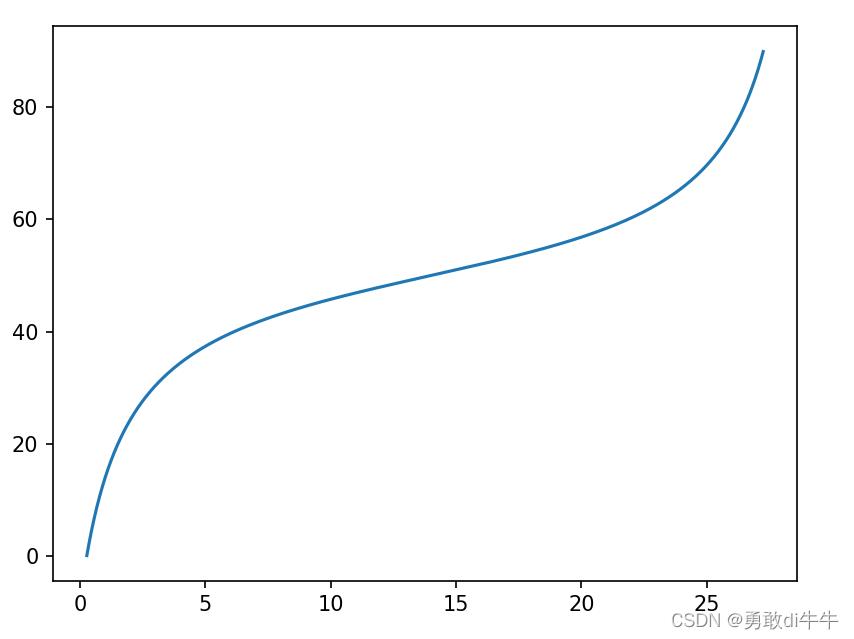
这是你一米二的弟弟：

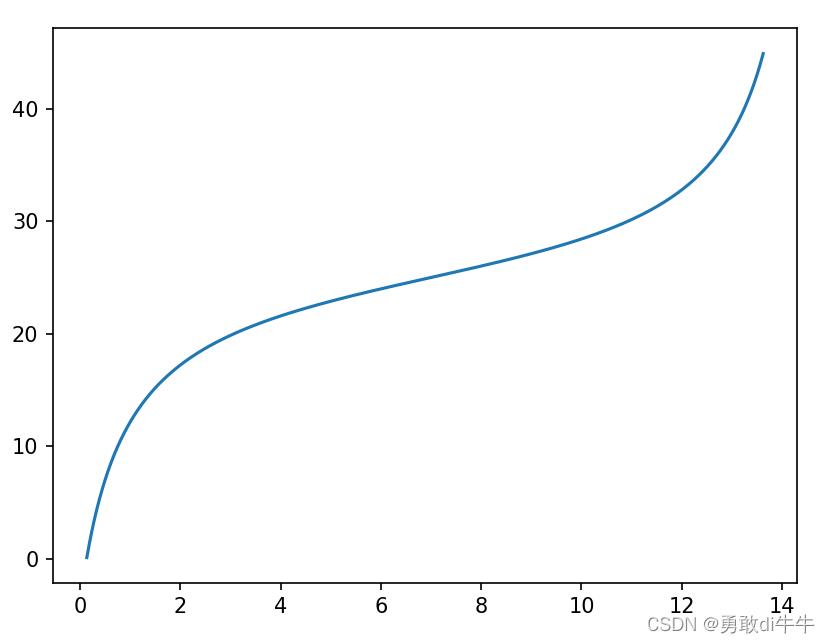
这是你一米六的女朋友：

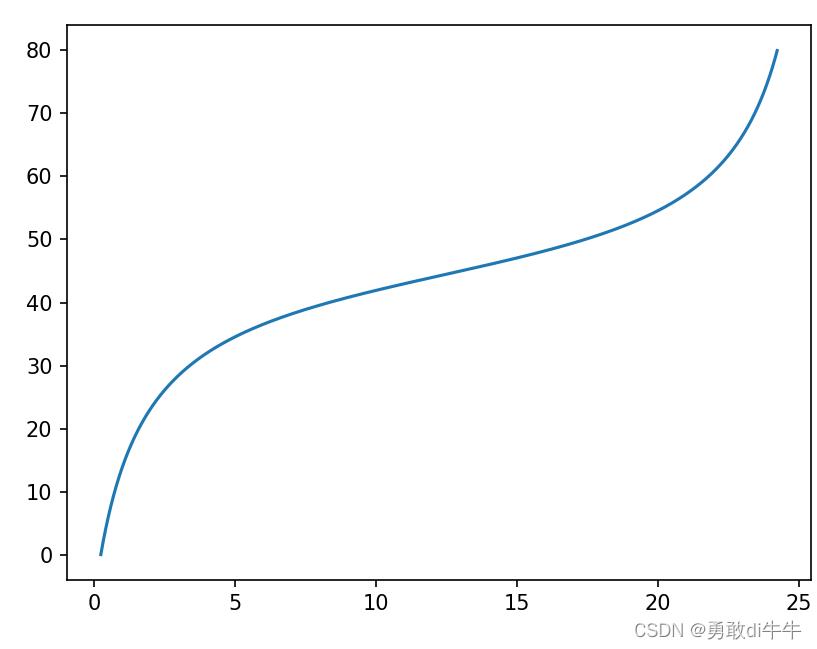
可以发现我们变换模型的身高，都保持了一致的曲线。

动态验证

我们每相隔0.1s打印一次，路径点：结果如图：

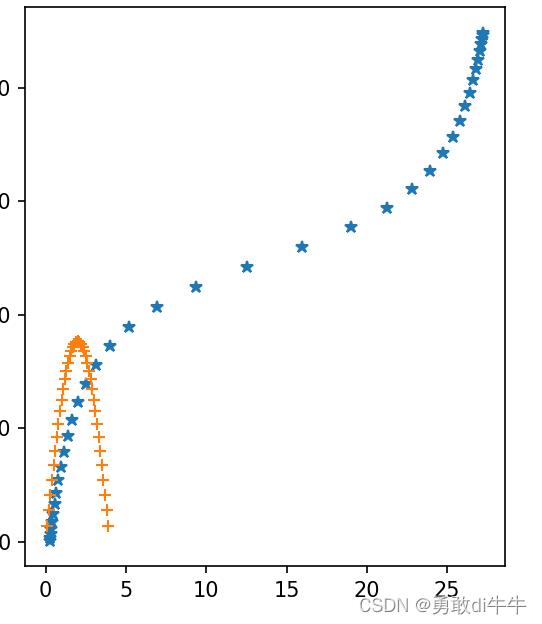
可以观察到中间的点较为稀疏，和我们的预期效果一样，这里我并没有直接用上面的微分方程，而是用微元法算的路径，原理很简单，我们小时候就学过，这里不再赘述，并且更换H，与T之后，误差也很小。
贴上代码：

import numpy as np
from matplotlib import pyplot as plt
import gif

H = 180

def path(H, T):
    # H是我们测试模型的身高
    listy = []
    t = np.arange(0.1,T,0.1)
    ys = H*(np.pi)/(4*T)*np.sin(t*np.pi/T)
    s = 0
    s0 = 0
    for i in ys:
        s = s + (i+s0)*0.1/2
        listy.append(s)
        s0 = i
    y = np.array(listy)

    # x = pow((pow(y,2) - 10*y + 26),-1)
    x = H / 18 * (np.arctan(18 * y / H - 5) + 1.4)
    return x,y,t,ys

x,y,t,ys= path(H,4)
print(y)

plt.plot(x,y,"*")
plt.plot(t,ys,"+")
plt.show()
    #plt.pause(0.01)片

制作偏移量生成工具

我们知道，数字雨的每一个数字都会在每一帧进行垂直移动，我们只要在想要进行潘周聃曲线的时候插入上面的偏移量即可。
原理是上面的这里直接上代码：

import numpy as np

def path(H, T, t0):
    # H是我们测试模型的身高
    listy = []
    t = np.arange(0, T, t0)
    ys = H * (np.pi) / (4 * T) * np.sin(t * np.pi / T)  # 垂直方向的速度函数
    y0 = 0
    for i in ys:
        s0 = (i + y0) * t0 / 2  # 垂直方向单位时间内移动距离
        listy.append(s0)
        y0 = i  # 记录前一次的速度
    s0 = 0
    s = 0
    listy0 = []
    for i in ys:
        s = s + (i+s0) * t0 / 2  # 垂直总路程
        listy0.append(s)
        s0 = i
    y = np.array(listy0)
    x = H / 18 * (np.arctan(18 * y / H - 5) + 1.4)
    x0 = 0
    listx = []
    for i in x:
        s0 = i - x0  # 水平方向单位时间内移动距离
        listx.append(s0)
        x0 = i  # 保存前一次的X坐标
    return listx, listy


print(path(100,5,0.1))

数字雨效果制作

哈哈哈，到这里我们的数字雨就变得妖娆起来啦，是不是有潘周耼的风范呢了，上代码：

import pygame
import random

# !/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Date  : 2018/10/23


import numpy as np

import random

import pygame


def path(H, T, t0):
    # H是我们测试模型的身高
    listy = []
    t = np.arange(0, T, t0)
    ys = H * (np.pi) / (4 * T) * np.sin(t * np.pi / T)  # 垂直方向的速度函数
    y0 = 0
    for i in ys:
        s0 = (i + y0) * t0 / 2  # 垂直方向单位时间内移动距离
        listy.append(s0)
        y0 = i  # 记录前一次的速度
    s0 = 0
    s = 0
    listy0 = []
    for i in ys:
        s = s + (i + s0) * t0 / 2  # 垂直总路程
        listy0.append(s)
        s0 = i
    y = np.array(listy0)
    x = H / 18 * (np.arctan(18 * y / H - 5) + 1.4)
    x0 = 0
    listx = []
    for i in x:
        s0 = i - x0  # 水平方向单位时间内移动距离
        listx.append(s0)
        x0 = i  # 保存前一次的X坐标
    return listx, listy


PANEL_width = 600
PANEL_highly = 500
FONT_PX = 15

pygame.init()

# 创建一个可视化窗口
winSur = pygame.display.set_mode((PANEL_width, PANEL_highly))

font = pygame.font.SysFont("123.ttf", 25)

bg_suface = pygame.Surface((PANEL_width, PANEL_highly), flags=pygame.SRCALPHA)

pygame.Surface.convert(bg_suface)

bg_suface.fill(pygame.Color(0, 0, 0, 28))

# winSur.fill((0, 0, 0))

# 数字版
# letter = [font.render(str(i), True, (0, 255, 0)) for i in range(10)]

# 字母版
letter = ['q', 'w', 'e', 'r', 't', 'y', 'u', 'i', 'o', 'p', 'a', 's', 'd', 'f', 'g', 'h', 'j', 'k', 'l', 'z', 'x', 'c',
          'v', 'b', 'n', 'm']
texts = [
    font.render(str(letter[i]), True, (0, 255, 0)) for i in range(26)
]

# 按屏幕的宽带计算可以在画板上放几列坐标并生成一个列表
column = int(PANEL_width / FONT_PX)
drops = [0 for i in range(column)]
print(drops)
pan = -1
x0 = 0
y0 = 0
i0 = 0
dropsx = [0 for i in range(column)]
dropsy = [0 for i in range(column)]
listx, listy = path(400, 2, 0.1)

kk = 0  # 获取之前的坐标
finsh = False
allfinish =False
while True:
    # 从队列中获取事件
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            exit()
        elif event.type == pygame.KEYDOWN:

            chang = pygame.key.get_pressed()
            if chang[32]:  # 按下空格键
                pan = 1000
                i0 = 5   # 取消密集点
    if pan > 0:
        pygame.time.delay(100)
        winSur.blit(bg_suface, (0, 0))
        pan = pan - 1
        if i0 < len(listx):
            x0 = listx[i0]
            y0 = listy[i0]
        else:
            finsh = True
        i0 = i0 + 1
        if kk == 0:
            for i in range(len(drops)):
                dropsx[i] = i * FONT_PX
                dropsy[i] = drops[i] * FONT_PX
            kk = 1

        if finsh:
            allfinish = True
            for i in range(len(drops)):
                text = random.choice(texts)
                dropsy[i] = dropsy[i] + FONT_PX
                dropsx[i] = dropsx[i]
                # 重新编辑每个坐标点的图像
                winSur.blit(text, (dropsx[i], dropsy[i]))
                if dropsy[i] > PANEL_highly and allfinish:  # 到头了
                    allfinish = True
                else:
                    allfinish =False
        for i in range(len(drops)):
            text = random.choice(texts)
            dropsy[i] = dropsy[i] + y0
            dropsx[i] = dropsx[i] + x0
            # 重新编辑每个坐标点的图像
            winSur.blit(text, (dropsx[i], dropsy[i]))
            # if drops[i] * 10 > PANEL_highly:  # 到头了，或者运气不好
            # drops[i] = 0
        if allfinish:
            pan = -1
            drops = [0 for i in range(column以上是关于潘周聃之Python分聃 -----数字雨加入潘周聃运动曲线的主要内容，如果未能解决你的问题，请参考以下文章 
 Python代写，Python作业代写，代写Python，代做Python
 Python开发
 Python,python,python
 Python 介绍
 Python学习之认识python
 python初识