区块链与密码学第8-3讲：AOS环签名算法

Posted 2022-05-09 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

8.3AOS环签名算法

2002年，Abe等基于离散对数问题开发了一种新型的环签名，他们使用因果环来达到效果。与早期的环签名相比，这种因果环的使用使签名的大小显著减少了（50%左右）。Abe等给出了一种通用环签名构造方法，利用该方法可以把任意数字签名转换为环签名，这里只介绍他们提出的基于Schnorr签名的环签名算法。首先回顾一下Schnorr签名算法：

假设p和q是大素数，且q能被p-1整除，q是大于等于160 bit的整数，p是大于等于512 bit的整数，保证GF(p)中求解离散对数困难；g是GF(p)中元素，且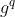≡1 mod p

密钥生成

①Alice选择随机数x为私钥，其中1<x<q

②Alice计算公钥y≡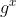 (mod p)

 

签名算法

①Alice首先随机数k，这里1<k<q

②Alice计算c=h(M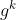， mod p) 

③Alice计算s=k - x · c ( mod q) 

④Alice输出签名(c,s)

验证算法

①Bob计算e = 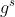 ·  mod p

②Bob验证c=h(M,e)是否成立，如果成立输出「Accept」，否则输出「Reject」

环签名算法

 

环验证算法

今天的课程就到这里啦，下节课我们将开始学习ZK环签名算法，敬请期待！

同学们可以关注点宽学园，每周持续更新区块链系列课程，小宽带你进入区块链世界。我们下节课见啦。

【区块链与密码学】课堂回顾：

区块链与密码学系列文章合集

创作打卡挑战赛 赢取流量/现金/CSDN周边激励大奖