强化学习 马尔可夫决策过程(MDP)是什么
Posted 软件工程小施同学
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了强化学习 马尔可夫决策过程(MDP)是什么相关的知识,希望对你有一定的参考价值。
2016 年上半年,李世石和 AlphaGo 的“人机大战”掀起了一波人工智能浪潮,也引起了大家对于人工智能的热烈讨论。本文主要学习人工智能中的强化学习,它是计算机以“试错”的方式进行学习,通过与环境进行交互获得的奖赏指导行为,目标是使计算机获得最大的奖赏。
以围棋为例,一个强化学习问题通常包含如下要素:
- 动作空间(Action Space):A,可以采取的所有合法动作的集合,所有合法的落子。
- 状态空间(State Space):S;所有的状态的集合称为状态空间,所有的棋盘布局。
- 奖励(Reward):R;胜利正向奖励,输了负向奖励。
- 状态转移概率矩阵(Transition):P。预判出对手可能的落子点,给每一种情况赋予一个概率。
而强化学习的目的就是让智能体通过不断的学习,找到解决问题的最好的步骤序列,这个“最好”的衡量标准就是智能体执行一系列动作后得到的累积奖励。
马尔可夫决策过程(Markov Decision Processes,MDP)是对强化学习中环境的形式化的描述,或者说是对于智能体所处的环境的一个建模。在强化学习中,几乎所有的问题都可以形式化地表示为一个马尔可夫决策过程。
“Frozen Lake”游戏的场景是一个结了冰的湖面(即 4×4 大小的方格),要求从开始点“Start”走到目标点“Goal”,且不能掉进冰窟窿里。

游戏有两种模式:“有风”模式和“无风”模式。两种模式的区别是,在“有风”模式下,智能体的移动会受到风的影响,例如,智能体当前的位置是 S3,智能体选择向右走一步,“无风”模式下智能体会到达 S4状态,而在“有风”模式下,智能体的位置就不确定了,有可能会被风吹到任意状态,例如 S7。
在“Frozen Lake”游戏中,智能体从“Start”走到目标点“Goal”需要经过一个序列的中间状态,同时也需要根据策略做出一系列的动作。通常根据智能体执行完一个序列的动作后所获得的累积奖励来评判这个策略的优劣,累积得到的奖励越大,则认为策略越优。
计算累积奖励有两种方式,一种是计算从当前状态到结束状态的所有奖励值之和:
Gt=rt+1+rt+2+...+rt+T
上面适用于有限时界(Finite-horizon)情况下的强化学习,但是在有些无限时界(Finite-horizon)情况,智能体要执行的可能是一个时间持续很长的任务,比如自动驾驶,如果使用上式计算累积奖励值显然是不合理的。
需要一个有限的值,通常会增加一个折扣因子,如下式:
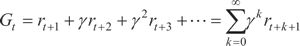
在上式中,0≤γ≤1 。当 γ 的值等于 0 时,则智能体只考虑下一步的回报;当 γ 的值越趋近于 1,未来的奖励就会被越多地考虑在内。需要注意的是,有时候我们会更关心眼下的奖励,有时候则会更关心未来的奖励,调整的方式就是修改 γ 的值。
先简化一下“Frozen Lake”(无风模式),并且不考虑起点和终点,如图 1 所示。

简化的“Frozen Lake”游戏
右侧的状态转换图,表示从每个状态转移到下一个状态的概率及能获得的相应奖励。例如在状态 S1 时,可以转移到 S2 状态,也可以转移到 S3 状态,或者不移动,留在 S1 状态,其概率分别为 0.3、0.5 和 0.2,获得的相应奖励分别为 2、2 和 1。对于每一个状态来说,出边的概率和必为 1。
1. 马尔可夫过程(Markov Process)
在一个随机过程 s0,s1,…,sn 中,已知时刻 ti 所处的状态 si,如果在时刻 ti+1 时的状态 si+1 只与状态 si 相关,而与 ti 时刻之前的状态无关,则称这个过程为马尔可夫过程(类递推)。
例如图 1 中的例子,智能体从 S1 状态移动到 S3 状态后,至于下一个状态是什么已经与 S1 无关了,只取决于当前的 S3 状态。这种特性称为随机过程的马尔可夫性(或称为“无后效性”)。具有马尔可夫性的随机过程 s0,s1,…,sn 称为马尔可夫链(Markov Chain)。
2. 马尔可夫回报过程(Markov Reward Process)
最简单的情况下,每执行一个动作后,到达的下一个状态是确定的,因此仅需要将智能体每一步获得的奖励累加起来。
然而,很多时候,状态是不确定的,例如在“Frozen Lake”游戏的“有风”模式下,智能体执行一个动作后会以一定的概率转移到另一个状态,因此,得到的奖励也与这个概率相关。所以在计算累积奖励的时候,通常是计算奖励的期望,用 V 表示奖励的期望,则状态 s 的期望奖励值表示为:V(s)=E[Gt|St=s]
所以 Gt=rt+1+rt+2+...+rt+T 可表示为如下形式:

“累积奖励”的第二个公式考虑折扣因子则表示为:

3. 马尔可夫决策过程(Markov Decision Process)
在简化游戏 中只考虑了“Frozen Lake”游戏的“无风”模式,因为在“无风”模式下,智能体执行了一个动作后到达的下一个状态是确定的,所以只考虑状态的转移而无须考虑具体的动作。然而在“有风”模式下,根据执行的动作不同,状态的转移概率也不同。
依然以简化后的“Frozen Lake”游戏例子,假如当前状态为 S1,在“有风”模式下,根据执行的动作不同,状态转移概率如表 1 所示。

什么是马尔可夫决策过程?我们将马尔可夫决策过程定义为一个五元组:M=(S,A,R,P,γ)
- S:状态空间,例如在“Frozen Lake”游戏中,总共有 16 个状态(Start,S2,…,S15,Goal);
- A:动作空间,在“Frozen Lake”游戏中,每个状态下可以执行的动作有四个(上、下、左和右);
- R:奖励函数,在某个状态 St 下执行了一个动作并转移到下一个状态 St+1,就会得到一个相应的奖励 rt+1;
- P:状态转移规则,可以理解为我们之前介绍的状态转移概率矩阵。在某个状态 St 下执行了一个动作,就会以一定的概率转移到下一个状态 St+1。
现在总结一下,强化学习要解决的问题是:智能体需要学习一个策略 π,这个策略 π 定义了从状态到动作的一个映射关系 π:S→A,也就是说,智能体在任意状态 st 下所能执行的动作为 at=π(st),并且有

。
用价值 Vπ 来衡量这个策略 π 的好坏,价值 Vπ(st) 代表的是智能体从状态 st 开始,在遵循策略 π 的前提下执行一系列动作后获得的累积奖励的期望值(事实上,当策略 π 确定后,MDP 中的状态转移概率也就确定了,此时可以简单地看成马尔可夫回报过程,即可使用求解马尔可夫回报过程的方法求解回报):
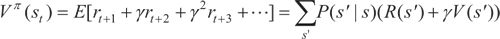
这里的价值是在遵循策略 π 的情况下的价值。
参考文章:
强化学习的基本概念(实例讲解)_Python教程网www.92python.com/view/409.html正在上传…重新上传取消
马尔可夫决策过程(MDP)_Python教程网www.92python.com/view/410.html正在上传…重新上传取消
发布于 2021-05-17 23:12
工种号:微程序学堂
以上是关于强化学习 马尔可夫决策过程(MDP)是什么的主要内容,如果未能解决你的问题,请参考以下文章