C++AVL Tree总结

Posted 2022-04-22 SuchABigBug

文章目录

• 一、AVL Tree概念
• 二、左/右单旋
• 三、左/右双旋

---

一、AVL Tree概念

上次我们介绍的二叉搜索树也有弊端，如果数据是有序或接近有序二叉搜索树将退化为单枝，相当于查找时在顺序表中搜索元素，效率变的很低。

我们这里介绍的AVL是一颗高度平衡的二叉搜索树，如果他有n个节点，其高度保持在O(log2n)，搜索时间复杂度为O(log2n)。

AVL树的要求是，保证每个节点的左右子树高低之差绝对值不超过1

具体在树的结构里面加入一个平衡因子，去衡量二叉树的左右高度差是不是超过1，通过右边高度来减左边高度

平衡因子 = 右树的高度 - 左树的高度

---

我们在做插入操作时和普通的二叉搜索树的区别：

现在思考一个问题，插入到9的左边或者右边有什么区别，parent的平衡因子会发生上面变化？

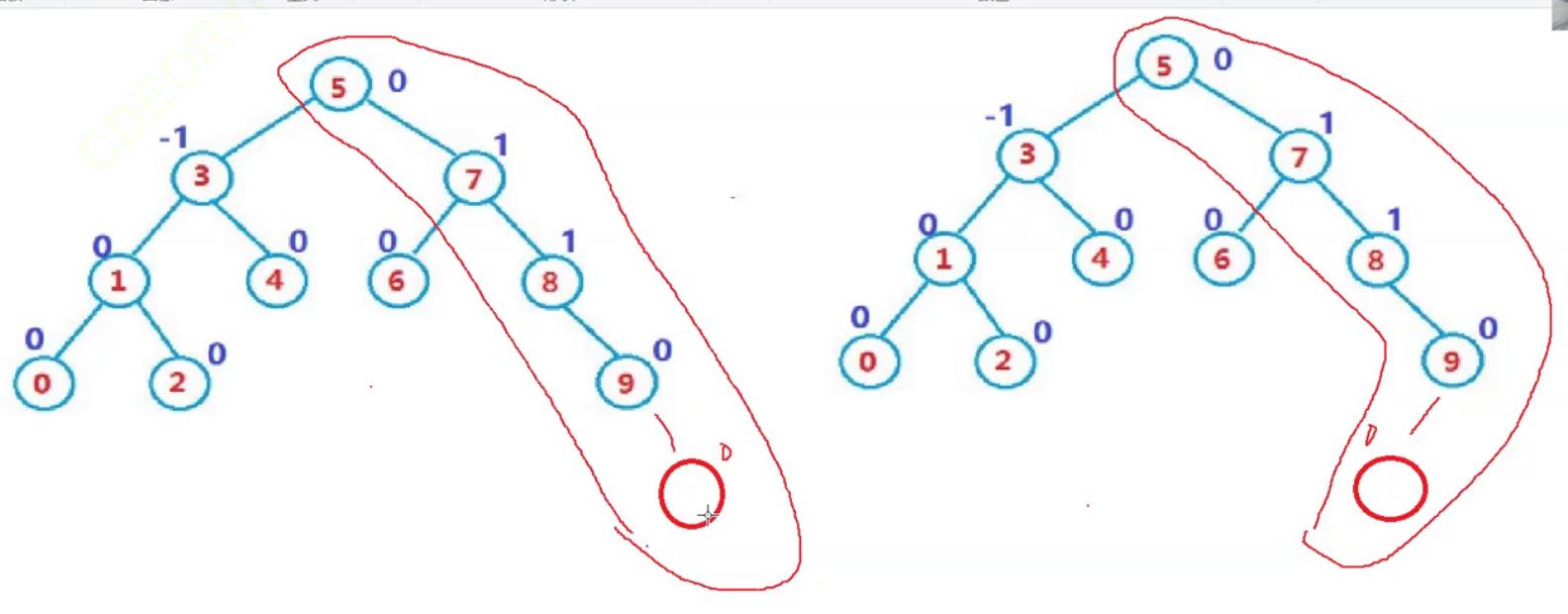
平衡因子 = 右 - 左， 父因子如果是1说明右边高了一个，-1说明左边高了一个

插入在9的左边，9的平衡因子 --，为 -1， 如果插入到右边，平衡因子++，为1

插入一个节点后，对新节点的祖先可能会有影响，需要更具体的分析：

1. 插入更新的节点在父亲的左边，父亲的平衡因子–
2. 插入更新的节点在父亲的右边，父亲的平衡因子++
3. 如果父亲的平衡因子更新后是1，或者-1，说明父亲所有子树高度变了，需要继续向上更新
4. 如果父亲平衡因子更新后，是0，说明父亲所有子树的高度没有变，不需要继续往上更新
5. 更新到根节点就不需要再更新
6. 更新后父亲的平衡因子是2或者-2，说明父亲所有的子树已经不平衡，需要旋转处理，让他们保持平衡

下面我们就需要讨论一下如何旋转，以达到平衡的目的

二、左/右单旋

给个右单旋的例子:

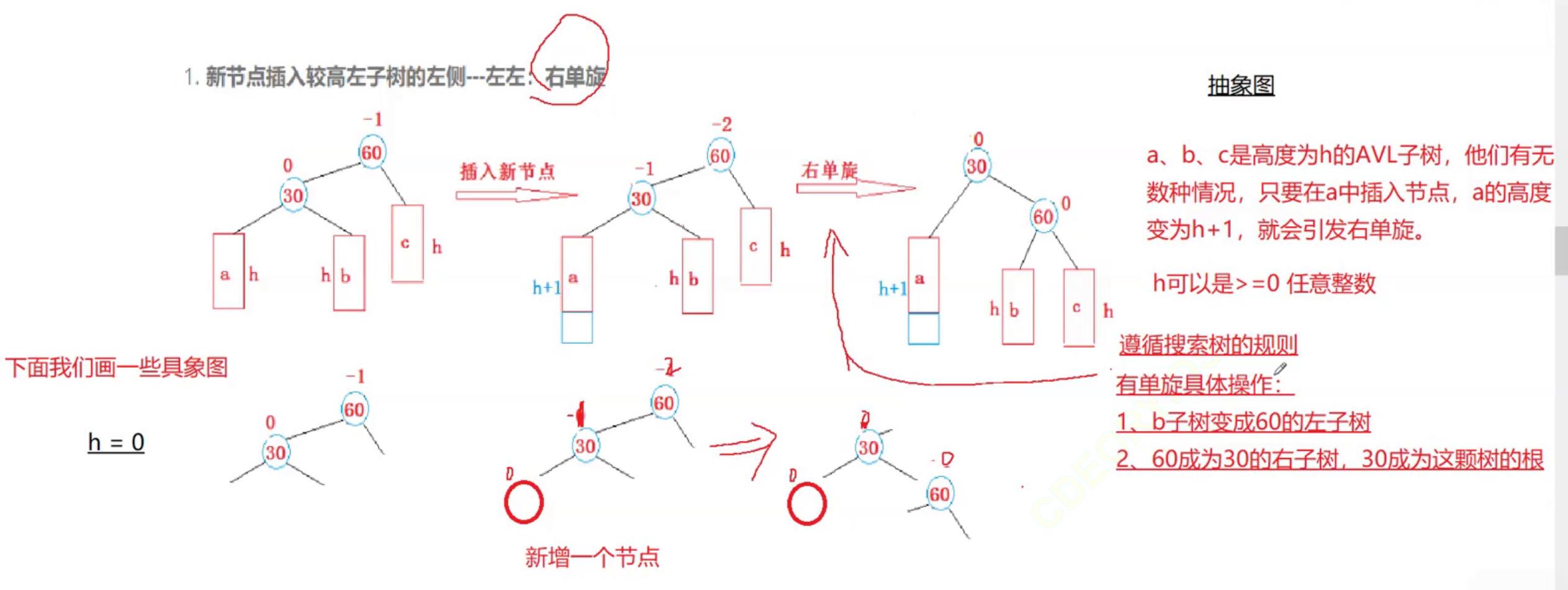
我们来一步步分析：

1. 根节点的平衡因子当前为-1，当我们在左子树的左边插入一个节点后引发右单旋
2. 此时节点30的平衡因子为-1，继续往上更新，根节点平衡因子更新成2，引发右单旋
3. 这里a、b、c是一个抽象的概念指高度为h的AVL子树(h>=0任意整数)，b子树变成60的左子树
4. 60成为30的右子树，此时30称为这棵树的根
5. 我们再看此时的根节点平衡因子就更新成了0时，停止更新

代码实现：

void RotateRight(Node* parent) 
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		//注意subLR有可能是空指针
		if (subLR) 
			subLR->_parent = parent;
		
		
		//假如当前的parent不是根，上面还有很多node
		Node* ppNode = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		//如果parent就是根
		if (parent == _root) 
			_root = subL;
			subL->_parent = nullptr;
		
		else 
			//判断当前的parent是在ppnode的左边还是右边
			if (ppNode->_left == parent) 
				ppNode->_left = subL;
			
			else 
				ppNode->_right = subL;
			
			subL->_parent = ppNode;
		

		//最后更新平衡因子
		parent->_bf = subL->_bf = 0;
	

同理左旋亦是如此。

三、左/右双旋

单旋的规律是线状的，那么双旋则是折线状的

上图可能比较容易混淆，我们来一步步分析：

1. 当前根节点平衡因子为-1，我们下步操作是在节点60下b子树中，增加一个节点后，节点30平衡因子为-1，根节点平衡因子变为-2，引发双旋
2. 我们先进行一个左单旋，然后再进行右单旋
3. 把b子树给节点30的右边，节点60成为节点90的左边，节点60的左边是节点30，此时30的bf为0，节点60和90的bf为-2
4. 再进行一个右单旋，把节点60的右子树c给节点90的左边，让节点60的左边指向节点30，节点60的右边指向节点90

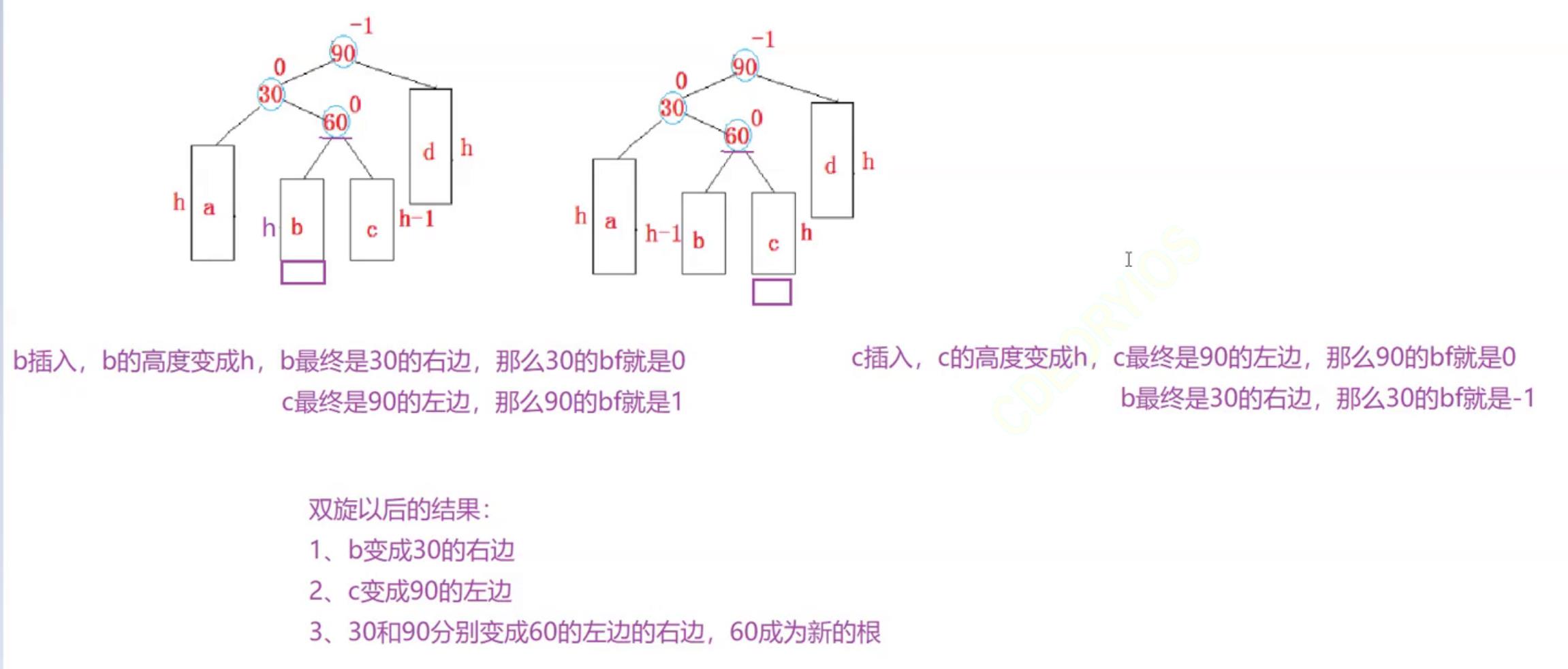
代码实现：

void RotateLeftThenRight(Node* parent) 
		
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		//先提前记录平衡因子
		int bf = subLR->_bf;

		RotateLeft(parent->_left);
		RotateRight(parent);

		//分三种情况
		//1. 如果是0，就说明本身就是一个新增
		if (bf == 0) 
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		
		else if (bf == -1) 
		//2. 如果是-1，说明在b插入，高度由原来的h-1变为h。 而30的左高度也是h，那么30bf为0
		
			subL->_bf = 0;
			parent->_bf = 1; // 左边为h，右边为h-1
			subLR->_bf = 0; // 任何情况都为0
		
		else if (bf == 1) 
			//说明在c插入
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		
		else 
			assert(false);
		

	

总结：

AVL的删除分三步：

1. 按照二叉搜索树的思路进行删除
2. 更新平衡因子
3. 如果出现不平衡树，进行旋转

---

click here Gitee链接🔗 🔗 🔗
👉 👉 👉 AVL Tree Gitee source code 👈 👈 👈

创作不易，如果文章对你帮助的话，点赞三连哦:)