数学之美：维特比和维特比算法

Posted 2022-04-22 青盏

维特比算法，现代数字通信中使用最频繁的算法，也是很多自然语言处理中的解码算法。由维特比大牛创建，今天的CDMA 3G通信标准就是由维特比创建的高通公司制定的。厉害的不行。维特比算法是一种特殊的但应用最广的动态规划算法。利用动态规划可以解决任何一个图中的最短路径问题，而维特比算法则是针对一种特殊的图——篱笆网络的有向图的最短路径问题提出的。之所以重要，是因为凡是使用隐马尔可夫模型描述的问题都可以用它来解码。

以拼音转汉字为例：

上图是一个很简单的隐马尔科夫模型，没有状态跳跃，也没有状态自环的问题。这个地方要说明一下，如果x认为是拼音的话，那么y就是对应的x的汉字，但是y并不是确定的。因为同一拼音可以有多种可能性的汉字，因此我们可以认为y输出的是一个关于拼音可能汉字字典的分布。这样我们可以假设xij为状态xi的第j个可能性取值，也就是y的取值。从而我们可以把上图转成如下篱笆图：

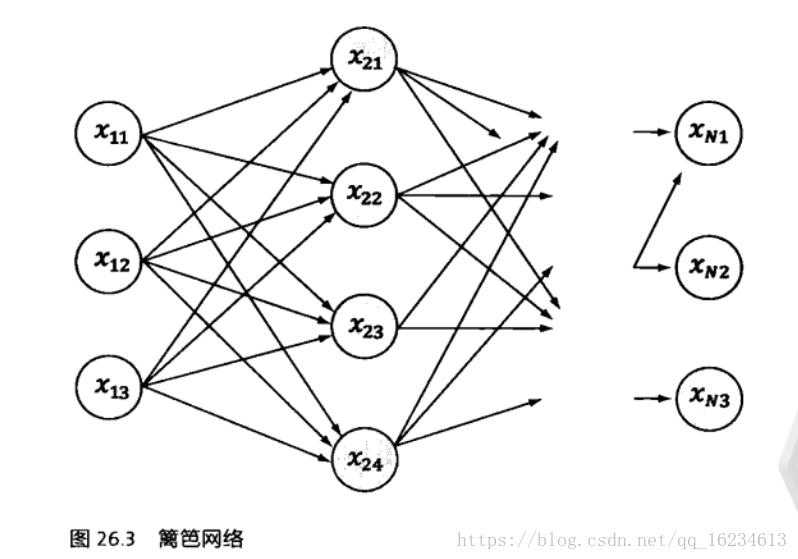
也就是每一列代表xi的可能性取值，x1与x2之间的连接，代表两个汉字之间存在的关系。从开始状态到最终状态可以产生很多条路径，每一条路径都代表一个可能的汉字序列。我们需要做的就是找出可能性最大的汉字序列。我们可以使用前面的公式计算出所有路径概率，选取最大的。但显然这些组合数非常多，使得序列状态数呈指数增长模式。因此需要一个最好能跟状态数成正比的算法。而维特比算法就于1967年提出。维特比算法具有如下特点：

学过图最短路径算法的很容易理解该算法。篱笆图有个特点，那就是不管最短路径是哪条，它必须通过篱笆图的每一列，也就是当i确定时，最短路径肯定要通过xij中的某一个j。这就有一个优点，就是我们只需要把每个xi中对应的所有j取值的当前最短路径记录下来，就可以在xi+1状态时很容易计算出xi+1状态所对应的j取值的最短路径计算出来。流程如下：

这种算法还有个优点就是解码过程是实时的。每打入一个拼音，算法就是解析出在该拼音xi下当前所有可能的最短路径。