SS-CA-APPLE:什么是柯西积分公式?
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SS-CA-APPLE:什么是柯西积分公式?相关的知识,希望对你有一定的参考价值。

§01 数学原理
1.1 柯西积分公式
1.1.1 定理
如果 f ( z ) f\\left( z \\right) f(z) 在区域 D D D 内处处解析, C C C 为 D D D 内的任意一条正向简单闭曲线,它的内部完全包含于 D D D , z 0 z_0 z0 为 C C C 内的任意点,那么 f ( z 0 ) = 1 2 π i ∮ C f ( z ) z − z 0 d z f\\left( z_0 \\right) = 1 \\over 2\\pi i\\oint_C f\\left( z \\right) \\over z - z_0 dz f(z0)=2πi1∮Cz−z0f(z)dz
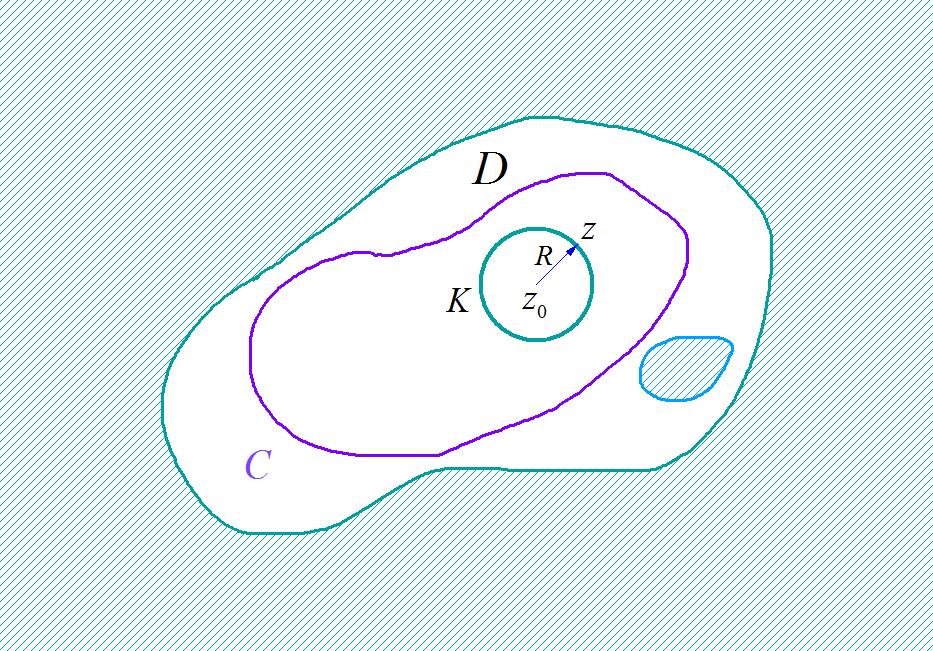
▲ 图1.1 柯西积分公式
证明: 由于 f ( z ) f\\left( z \\right) f(z) 在 z 0 z_0 z0 连续,任意给 ε > 0 \\varepsilon > 0 ε>0 ,必有一个 δ ( ε ) > 0 \\delta \\left( \\varepsilon \\right) > 0 δ(ε)>0 ,当 ∣ z − z 0 ∣ < δ \\left| z - z_0 \\right| < \\delta ∣z−z0∣<δ 时, ∣ f ( z ) − f ( z 0 ) ∣ < ε \\left| f\\left( z \\right) - f\\left( z_0 \\right) \\right| < \\varepsilon ∣f(z)−f(z0)∣<ε 。设以 z 0 z_0 z0 为中心, R R R 为半径的圆周 K : ∣ z − z 0 ∣ = R K:\\left| z - z_0 \\right| = R K:∣z−z0∣=R 全部位于 C C C 的内部,且 R < δ R < \\delta R<δ ,那么 ∮ C f ( z ) z − z 0 d z = ∮ K f ( z ) d z z − z 0 = ∮ K f ( z 0 ) d z z − z 0 + ∮ C f ( z ) − f ( z 0 ) z − z 0 d z \\oint_C f\\left( z \\right) \\over z - z_0 dz = \\oint_K f\\left( z \\right)dz \\over z - z_0 = \\oint_K f\\left( z_0 \\right)dz \\over z - z_0 + \\oint_C f\\left( z \\right) - f\\left( z_0 \\right) \\over z - z_0 dz ∮Cz−z0f(z)dz=∮Kz−z0f(z)dz=∮Kz−z0f(z0)dz+∮Cz−z0f(z)−f(z0)dz = 2 π i f ( z 0 ) + ∮ K f ( z ) − f ( z 0 ) z − z 0 d z = 2\\pi if\\left( z_0 \\right) + \\oint_K f\\left( z \\right) - f\\left( z_0 \\right) \\over z - z_0 dz =2πif(z0)+∮K以上是关于SS-CA-APPLE:什么是柯西积分公式?的主要内容,如果未能解决你的问题,请参考以下文章