计算机视觉教程0-3：为何拍照会有死亡视角？详解相机矩阵与畸变

Posted 2022-04-18 Mr.Winter`

---

目录

• 0 拍照的死亡角度
• 1 透视相机模型
• 2 相机矩阵
• 3 镜头畸变

0 拍照的死亡角度

拍照死亡角度一般指的是将自己脸盆子拍得特别大，拍出用鼻孔看人的狰狞面目，比如下面这张照片。在拍照的死亡角度下，镜头畸变会产生失真，让你的体态更圆润、厚实，因此部分美颜软件里人像修正中会有“去畸变”这一项功能。本文就从计算机视觉的角度谈一谈镜头畸变原理。

1 透视相机模型

透视相机模型描述了三维空间中的点与二维图像平面上像素间的映射关系。

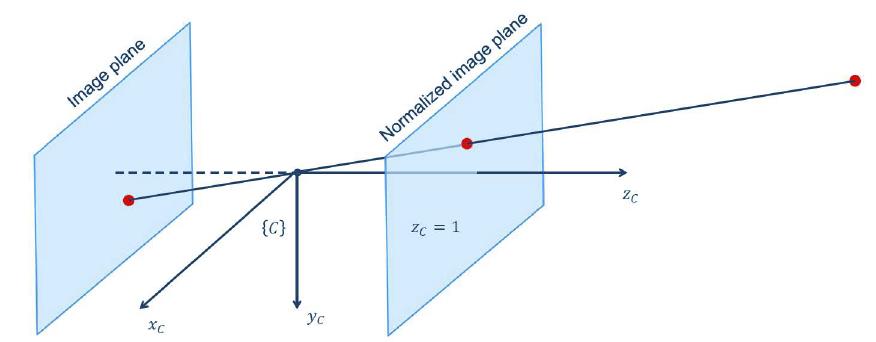
根据小孔成像原理，透视相机的成像点与空间点之间方向相反，如图所示。为得到与空间点方向相同的成像点，将成像面沿着光轴移动到归一化成像面，接下来的讨论以归一化成像面为准。

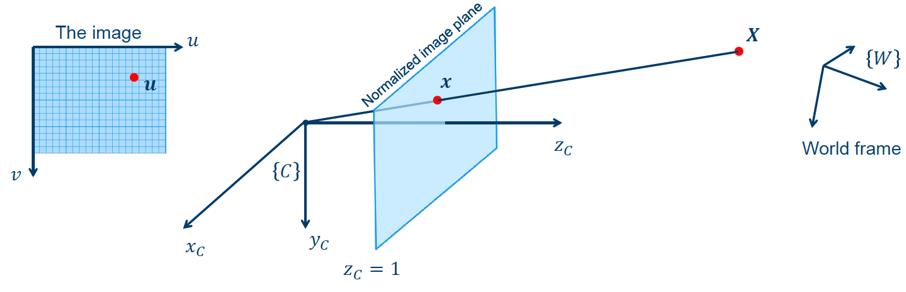
在确定归一化成像面后，从空间点${}^W\tilde{X}$到像素点$\tilde{u}$的映射可分为两步：

1. 将${}^W\tilde{X}$映射到归一化成像面的成像点${}^C\tilde{x}$，对应的映射关系称为相机外参(Extrinsic)；
2. 将${}^C\tilde{x}$映射到像素平面的像素$\tilde{u}$，对应的映射关系称为相机内参(Intrinsic)。上述各点均处于投影空间，采用齐次坐标。

2 相机矩阵

设世界坐标系$\mathbf{W}$相对于透视相机坐标系$\mathbf{C}$的位姿为

$${}_{\mathbf{W}}^{\mathbf{C}}\mathbf{T}=\left[\begin{array}{cc}{}_{\mathbf{W}}^{\mathbf{C}}\mathbf{R}& {}^{\mathbf{C}}{\mathbf{p}}_{w_0}\\ 0& 1\end{array}\right]$$

考虑到从三维空间降维到二维平面，设世界坐标值${\left[\begin{array}{cccc}{}^{\mathbf{W}}X& {}^{\mathbf{W}}Y& {}^{\mathbf{W}}Z& 1\end{array}\right]}^T$，则

$${}^{\mathbf{C}}\tilde{x}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]{,}_{\mathbf{W}}^{\mathbf{C}}{\mathbf{T}}^{\mathbf{W}}\tilde{X}=\left[\begin{array}{c}{}^{\mathbf{C}}X\\ {}^{\mathbf{C}}Y\\ {}^{\mathbf{C}}Z\end{array}\right]$$

在上述推导过程中，称

$${\mathbf{M}}_{\mathbf{E}}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]{,}_{\mathbf{W}}^{\mathbf{C}}\mathbf{T}=\left[\begin{array}{cc}{}_{\mathbf{W}}^{\mathbf{C}}\mathbf{R}& {}^{\mathbf{C}}{\mathbf{p}}_{w_0}\end{array}\right]$$

为相机外参矩阵。通常令尺度因子${}^{\mathbf{C}}Z=1$，${}^{\mathbf{C}}\tilde{x}=[\begin{array}{c}\frac{{}^{OpenGL\; 与\; OpenCV\; 相结合的计算机视觉教程\; [关闭]}}{{}^{\mathbf{C}}Z}\end{array}$

计算机视觉教程2-7：天使与恶魔?图文详解图像形态学运算(附代码)

计算机视觉教程3-1：全面详解图像边缘检测算法(附Python实战)

计算机视觉系列教程2-2：详解图像滤波算法(附Python实战)

PyTorch 计算机视觉的迁移学习教程代码详解 （TRANSFER LEARNING FOR COMPUTER VISION TUTORIAL ）

SLAM入门之视觉里程计：基础矩阵的估计