十大经典排序算法

Posted 2022-04-17 yangbocsu

十大经典排序算法

• 一、冒泡排序
• • 1.1 思想
  • 1.2 参考代码
  • 1.3 复杂度
• 二、选择排序
• • 2.1 思想
  • 2.2 参考代码
  • 2.3 复杂度
• 三、插入排序
• • 3.1 思想
  • 3.2 参考代码
  • 3.3 复杂度
• 四、希尔排序
• • 4 .1 思想
  • 4.2 参考代码
  • 4.3 复杂度
• 五、快速排序
• • 5.1 思想
  • 5.2 参考代码
  • 5.3 复杂度
• 六、归并排序
• • 6.1 思想
  • 6.2 参考代码
  • 6.3 复杂度
• 七、桶排序
• • .1 思想
  • .2 参考代码
  • .3 复杂度
• 八、堆排序
• • .1 思想
  • .2 参考代码
  • .3 复杂度
• 九、计数排序
• • .1 思想
  • .2 参考代码
  • .3 复杂度
• 十、基数排序
• • .1 思想
  • .2 参考代码
  • .3 复杂度

---

默认从小排到大。

---

一、冒泡排序

1.1 思想

• 两两相互比较；
• 大数都往后扔；

1.2 参考代码

	// 冒泡排序
    public static int[] BubbleSort(int[] nums)
        for (int i = 0; i < nums.length; i++) 
            for (int j = 0; j < nums.length-1-i; j++) 
                if(nums[j]> nums[j+1])
                    int temp = nums[j];
                    nums[j] = nums[j+1];
                    nums[j+1] = temp;
                
            
        
        return nums;
    

1.3 复杂度

时间复杂度: O(n²)
空间复杂度：O(1)

由于冒泡排序只会交换相邻的元素，它不会出现两个相等的元素，后面的元素被交换到前面去的情况，所以冒泡排序是稳定的。

---

二、选择排序

2.1 思想

• 每一轮找出最小元素的下标；
• 再与当前索引位置元素进行交换。

2.2 参考代码

	// 选择排序
    public static int[] SelectSort(int[] nums)
        for (int i = 0; i < nums.length; i++) 
            int minIndex = i;
            for (int j = i; j < nums.length; j++) 
                if(nums[j] < nums[minIndex])
                    minIndex = j;
                
            
            int temp = nums[i];
            nums[i] = nums[minIndex];
            nums[minIndex] = temp;
        
        return nums;
    

2.3 复杂度

时间复杂度: O(n²)
空间复杂度：O(1)

由于选择排序只会选择最小的元素进行交换，如果我们可以保证我们每次选择到的最小元素是第一次出现的（就算后面出现大小相等的元素我们也不会选择后面的），那么就可以保证它的稳定性，所以选择排序是可以做到稳定的。

---

三、插入排序

3.1 思想

• 依次选择一个元素，插入到前面已经排好序的数组中去；

3.2 参考代码

    //插入排序
    public static int[] InsertSort(int[] nums)
        // 默认第一个元素是有序的，从第二个元素开始遍历
        for (int i = 1; i < nums.length; i++) 
            int temp = nums[i];
            int j = i-1;
            // 如果当前元素比前一个元素小，则将前一个元素后移一位
            while (j >= 0 && nums[j] > temp)
                nums[j+1] = nums[j];
                j--;
            
            nums[j+1] = temp;
        
    

3.3 复杂度

时间复杂度: O(n²)
空间复杂度：O(1)

由于插入排序只会选择元素插入到适合的位置，只要我们按照原来的顺序遍历，即使相等的两个元素最后排完顺序之后，也会保持原有的相对顺序，所以插入排序是稳定的。

---

四、希尔排序

4 .1 思想

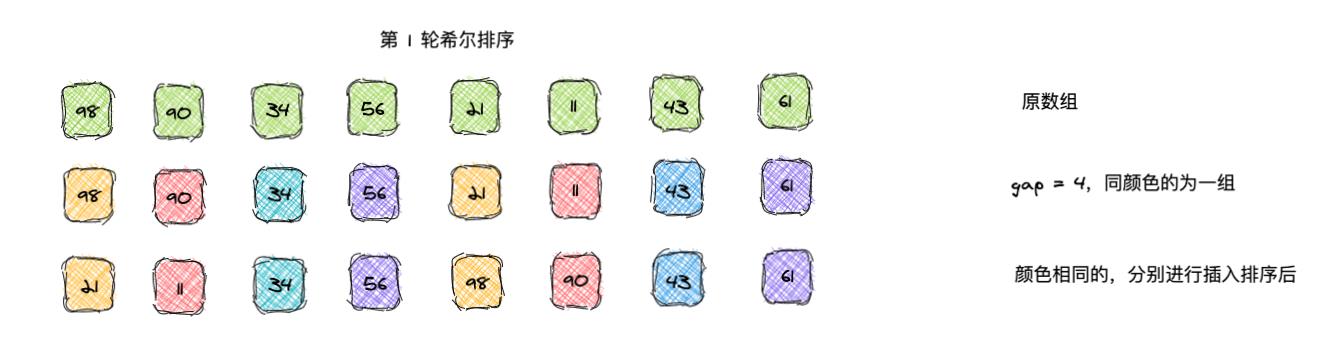
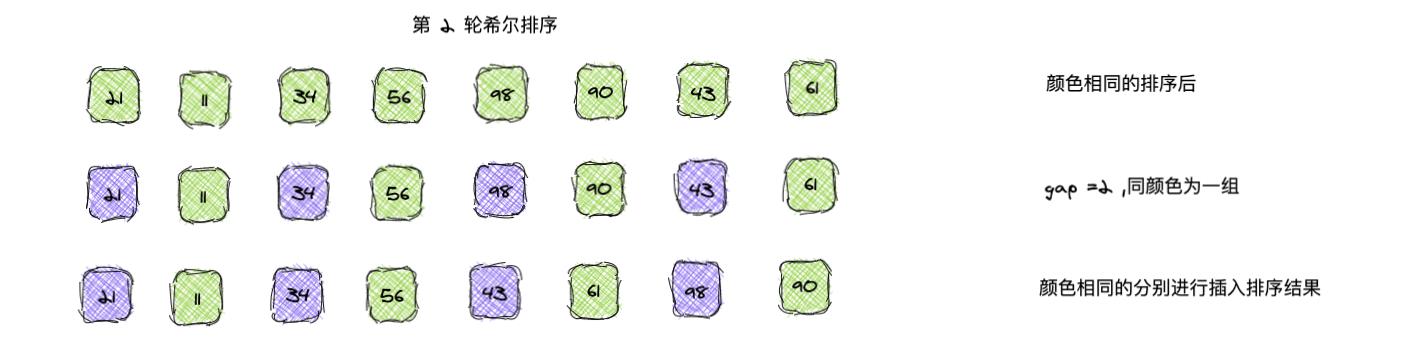
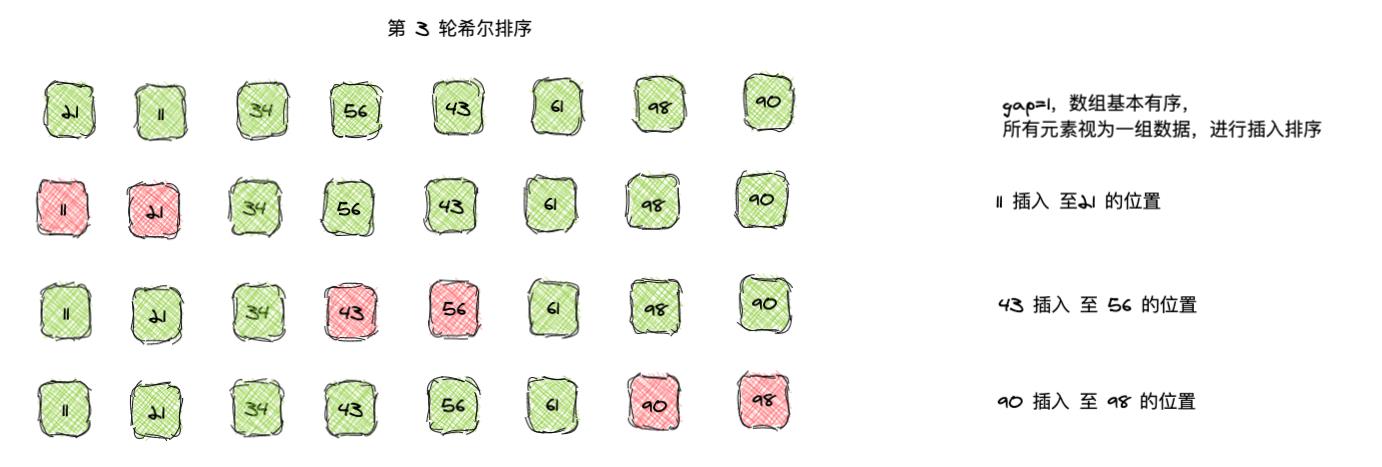
• 希尔排序是在数组中采用跳跃式分组，按照某个增量 gap 进行分组，分为若干组，每一组分别进行插入排序。
• 再逐步将增量 gap 缩小，再每一组进行插入排序，循环这个过程，直到增量为 1。

数组 [98，90，34，56，21，11，43，61]

4.2 参考代码

    // 希尔排序
    public static int[] ShellSort(int[] nums)
        for (int gap = nums.length; gap >0 ; gap /= 2) 
            for (int i = gap; i < nums.length ; i++) 
                int temp = nums[i];
                int j = i-gap;
                while (j >= 0 && nums[j] > temp)
                    nums[j+gap] = nums[j];
                    j -= gap;
                
                nums[j+gap] = temp;
            
        
        return nums;
    

4.3 复杂度

平均时间复杂度:O(n^3/2)
空间复杂度：O(1)

由于希尔排序，在分组的时候，会将后面的元素间隔性的调动到前面，所以会打乱原本两个相等的数之间的相对顺序，所以希尔排序是不稳定的排序算法。

---

五、快速排序

5.1 思想

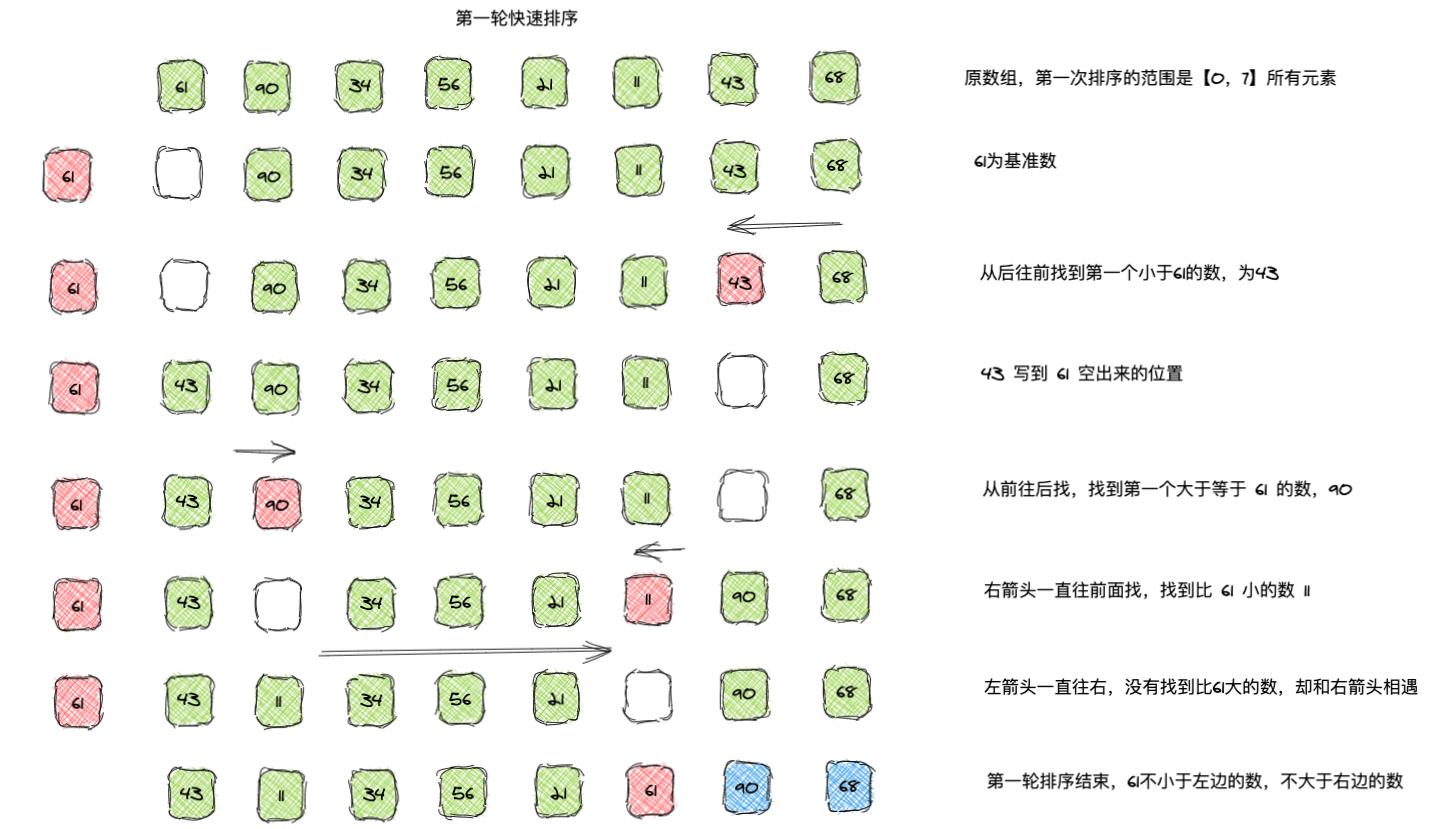
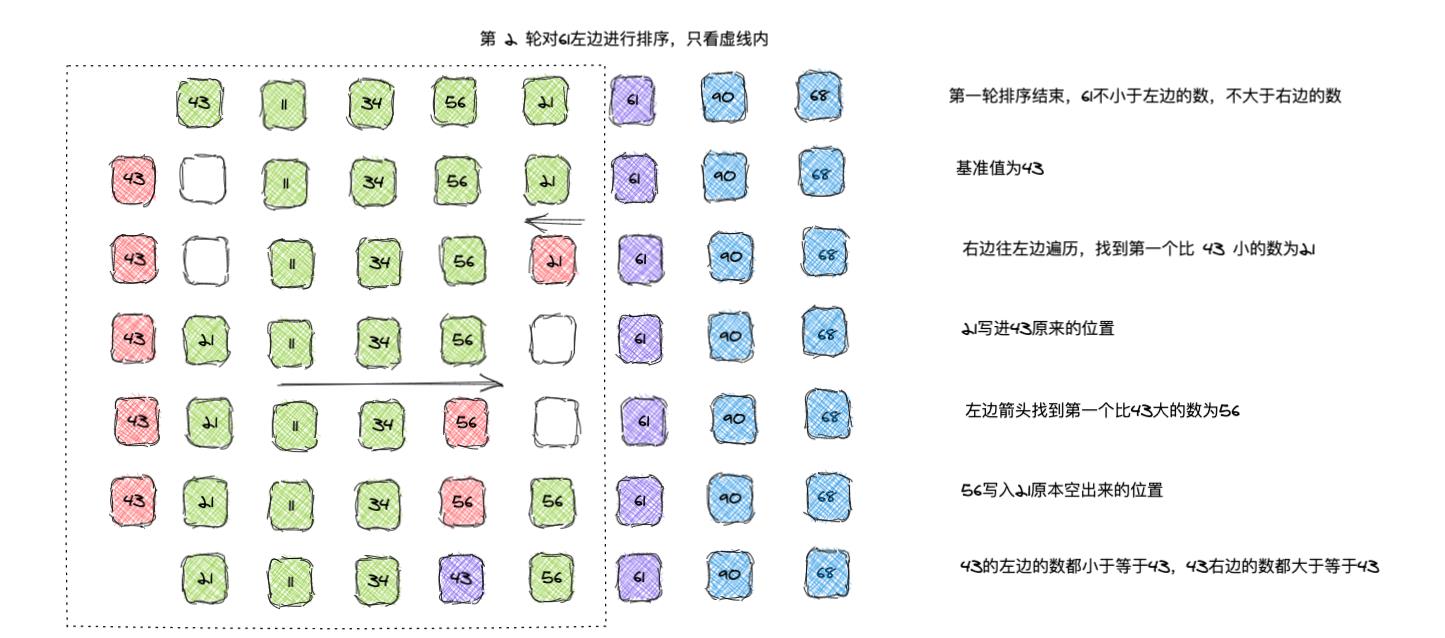
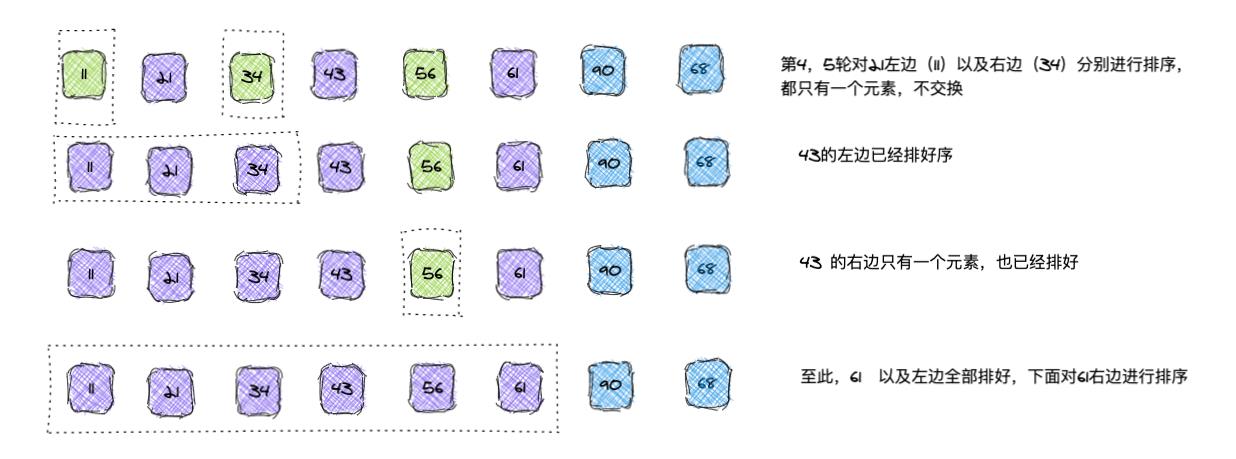
• 选择数组的一个数作为基准数，一趟排序，将数组分割成为两部分，一部分均小于/等于基准数，另外一部分大于/等于基准数；
• 然后分别对基准数的左右两部分继续排序，直到数组有序；
• 这体现了分而治之的思想，其中还应用到挖坑填数的策略。

5.2 参考代码

    // 快速排序
    public static int[] QuickSort(int[] nums)
        quickSort(nums, 0, nums.length-1);
        return nums;
    
    public static void quickSort(int[] nums, int left, int right)
        if(left >= right)
            return;
        
        // 取基准数
        int standardNum = nums[left];
        int i = left;
        int j = right;
        //
        while (i < j)
            // 如果 当前数 比 基准数 大，则继续向前找
            while (i < j && nums[j] >= standardNum)
                j--;
            
            nums[i] = nums[j];// 将比基准数小的数放到前面
            while (i < j && nums[i] <= standardNum)
                i++;
            
            nums[j] = nums[i];
        // 当i=j时，循环结束，i和j相等，此时i和j位置的数就是基准数
        
        nums[i] = standardNum;
        
        quickSort(nums, left, i-1);//对基准数左边的数组进行排序
        quickSort(nums, i+1, right);//对基准数右边的数组进行排序
    

5.3 复杂度

由于快速排序会将一个数大间隔的移动到一边，大的数放在右边，小的数放在左边，所以会破坏两个相等的元素的相对顺序，所以它是不稳定的排序算法。

---

六、归并排序

6.1 思想

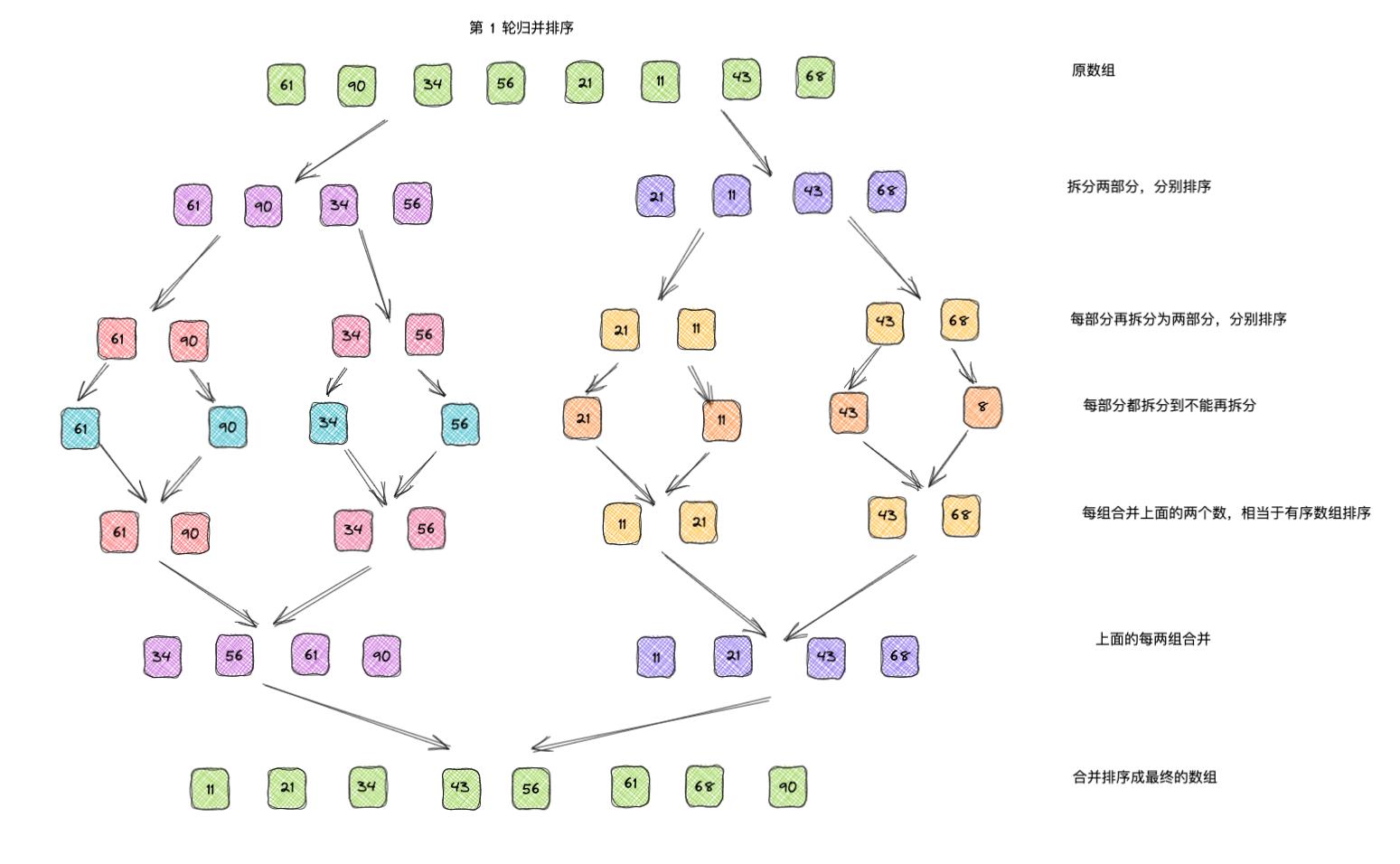
• 先将数组分割，再分割 … 分割到一个元素，然后再两两归并排序，做到局部有序；
• 不断地归并，直到数组又被全部合起来。
  

6.2 参考代码

    // MergeSort 归并排序
    public static int[] mergeSort(int[] arr, int l, int r) 
        if (l < r) 
            int mid = (l + r) / 2;
            // 左边归并排序
            mergeSort(arr, l, mid);
            // 右边归并排序
            mergeSort(arr, mid + 1, r);
            // 合并
            merge(arr, l, mid, r);
        
        return arr;
    

    public static void merge(int[] arr, int l, int mid, int r) 
        // 申请临时数组
        int[] temp = new int[r - l + 1];
        int i = l;
        int j = mid + 1;
        int k = 0;
        //比较左右两部分的元素，哪个小，就把那个元素填入temp中
        while (i <= mid && j <= r) 
            // 左边的元素小
            if (arr[i] < arr[j]) 
                temp[k++] = arr[i++];
            
            // 右边的元素小
            else 
                temp[k++] = arr[j++];
            
        
        // 如果左边还有元素剩下，则全部合并过去
        while (i <= mid) 
            temp[k++] = arr[i++];
        
        // 如果右边还有元素剩下，则全部合并过去
        while (j <= r) 
            temp[k++] = arr[j++];
        

        // 将temp中的元素全部拷贝到原数组中
        for (int m = 0; m < temp.length; m++) 
            arr[l + m] = temp[m];
        
    

6.3 复杂度

时间复杂度: O(nlog2n)
空间复杂度：O(n)

由于归并排序只会在相邻的子数组做合并操作，而且是严格按照从左到右的顺序，不会出现跳跃交换的情况，所以归并算法是稳定的排序算法。

---

七、桶排序

.1 思想

.2 参考代码

.3 复杂度

---

八、堆排序

.1 思想

.2 参考代码

.3 复杂度

---

九、计数排序

.1 思想

.2 参考代码

.3 复杂度

---

十、基数排序

.1 思想

.2 参考代码

.3 复杂度

---