Python: 向量矩阵和多维数组(基于NumPy库)
Posted 肉丸不肉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python: 向量矩阵和多维数组(基于NumPy库)相关的知识,希望对你有一定的参考价值。
参考文章:
- 数值 Python: 向量、矩阵和多维数组
- Numpy 中的矩阵向量乘法
- 对NumPy中dot()函数的理解
- np.random.rand()函数
- numpy.array函数详解
- numpy常用函数之arange函数
- 对NumPy中dot()函数的理解
- Python之numpy库——numpy.exp()函数
一/numpy数组对象
- 创建数组
- 在许多情况下,需生成一些元素遵循某些给定规则的数组,例如填充常量值,增加整数,统一间隔数字,随机数等。

- numpy.array函数详解:numpy.array(object, dtype=None, copy=True, order=‘K’, subok=False, ndmin=0)
- 作用:创建一个数组。
- 返回值:out:ndarray

- 填充常量的数组:np.zeros((2, 3)) 或者 np.zeros((2,3), dtype=np.float32)
In [11]: np.zeros((2, 3)) 或者 np.zeros((2,3),dtype=np.float32)
Out[11]:
array([[0., 0., 0.],
[0., 0., 0.]])
In [12]: np.ones(4)
Out[12]: array([1., 1., 1., 1.])
In [13]: np.ones(4, dtype=np.int64)
Out[13]: array([1, 1, 1, 1], dtype=int64)
- 由增量序列填充的数组:
In [24]: np.arange(0.0, 10, 1)
Out[24]: array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
In [26]: np.linspace(0, 10, 11)
Out[26]: array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
In [28]: np.linspace(0, 10, 21)
Out[28]:
array([ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. ,
5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5, 10. ])
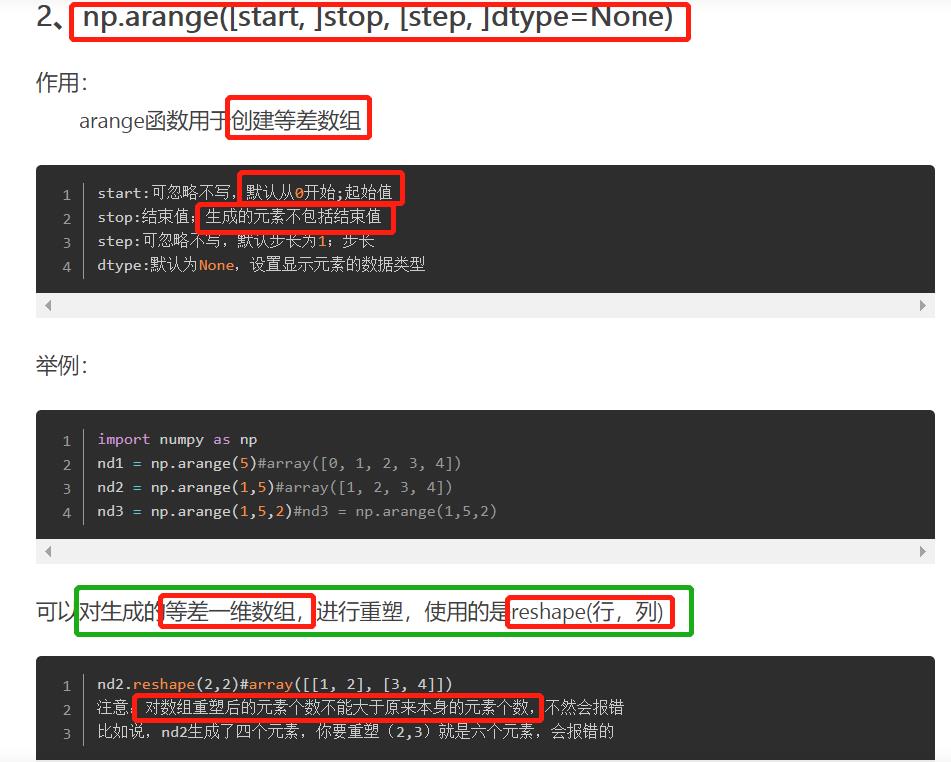
- 以数组形式处理数据时,对数组进行重新排列是很常见的。下表给出了 NumPy 中一些处理重排的函数。

- numpy提供了numpy.concatenate((a1,a2,…), axis=0)函数。能够一次完成多个数组的拼接。其中a1,a2,…是数组类型的参数。
>>> a=np.array([1,2,3])
>>> b=np.array([11,22,33])
>>> c=np.array([44,55,66])
>>> np.concatenate((a,b,c),axis=0) # 默认情况下,axis=0可以不写
array([ 1, 2, 3, 11, 22, 33, 44, 55, 66]) #对于一维数组拼接,axis的值不影响最后的结果
>>> a=np.array([[1,2,3],[4,5,6]])
>>> b=np.array([[11,21,31],[7,8,9]])
>>> np.concatenate((a,b),axis=0)
array([[ 1, 2, 3],
[ 4, 5, 6],
[11, 21, 31],
[ 7, 8, 9]])
>>> np.concatenate((a,b),axis=1) #axis=1表示对应行的数组进行拼接
array([[ 1, 2, 3, 11, 21, 31],
[ 4, 5, 6, 7, 8, 9]])
重排数组不需要修改底层数组数据,它只是通过重新定义数组的 strides 属性,改变了数据的解释方式。
In [24]: data = np.array([[1, 2], [3, 4]])
In [25]: np.reshape(data, (1, 4))
Out[25]: array([[1, 2, 3, 4]])
In [26]: data.reshape(4)
Out[26]: array([1, 2, 3, 4])
所指定的新形状必须与原始数组元素总数相匹配。需要注意的是,重排数组产生的是视图,如果需要数组的独立副本,则必须显式复制(例如,使用 np.copy)。
np.ravel(及其相应的 ndarray 方法)是重排的一种特殊情况,它会折叠数组的所有维并返回扁平的一维数组,其长度与原始数组中的元素总数相对应。ndarray 的方法 flatten 具有相同的功能,但返回的是副本而不是视图。
In [27]: data = np.array([[1, 2], [3, 4]])
In [28]: data
Out[28]:
array([[1, 2],
[3, 4]])
In [29]: data.flatten()
Out[29]: array([1, 2, 3, 4])
In [30]: data.flatten().shape
Out[30]: (4,)
-
NumPy 中多维数组的主要数据结构是 ndarray 类。除了存储在数组中的数据之外,该数据结构还包含有关数组的重要元数据,例如其形状、大小、数据类型以及其他属性。有关这些属性的更详细说明,请参阅下表。ndarray docstring 中提供了具有描述的完整属性列表,在 Python 解释器中通过 np.ndarray 调出;在 IPython 控制台通过 np.ndarray? 调出。

-
数据类型:
下表中展示了 NumPy 支持的基本数值数据类型:
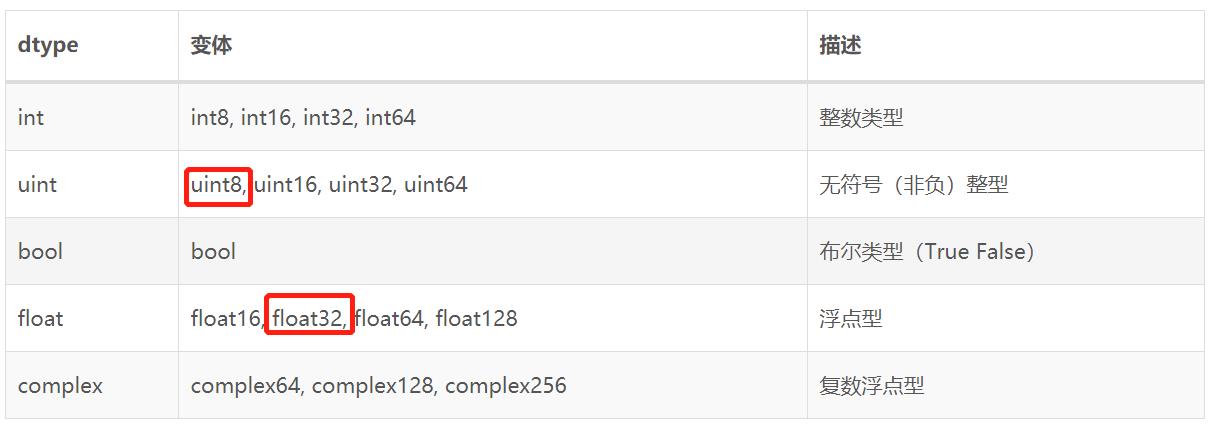
- NumPy 数组一旦创建其 dtype 就不能改变,但可以使用 type-casted 创建一个拷贝(也可以使用 ndarray 的 astype 属性)。
- 使用 NumPy 数组进行计算时,如果需要,数据类型可能会发生转换。
In [11]: np.array([1, 2, 3], dtype=np.int)
Out[11]: array([1, 2, 3])
In [18]: data.astype(np.float)
Out[18]: array([1., 2., 3.])
二/索引与切片
NumPy 数组的元素和子数组可以使用标准的方括号表示法来访问,该表示法也用于 Python 列表。在方括号内,各种不同的索引格式用于不同类型的元素选择。通常,括号内的表达式是一个元组,元组中每一项都指定了数组中相应维(轴)需要选择哪些元素。
- 一维数组
沿着单个轴,使用整数来选择单个元素,并且使用所谓的切片来选择元素的范围和序列。正整数用于从数组的开头索引元素(索引从 0 开始),负整数用于从数组末尾索引元素,最后一个元素用 -1 索引,倒数第二个元素用 -2 索引,依此类推。
切片的使用:符号也用于 Python 列表。 在这种表示法中,可以使用像 m: n 这样的表达式来选择一系列元素,选择的是以 m 开头并以 n-1 结尾的元素(注意不包括第 n 个元素)。 切片 m: n 也可以更明确地写为 m: n: 1,其中数字 1 表示应该选择 m 和 n 之间的每个元素。要从 m 和 n 之间每两个元素选择一个,请使用 m: n: 2,p 个元素,则使用 m: n: p。 如果 p 为负数,则元素以从 m 到 n+1 的反序返回(这意味着 m 大于 n)。有关 NumPy 阵列的索引和分片操作的概述,请参见下表。

In [58]: a = np.arange(0, 10)
In [59]: a
Out[59]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [60]: a[::-1]
Out[60]: array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
- 多维数组
array([[ 0, 1, 2, 3, 4, 5],
[10, 11, 12, 13, 14, 15],
[20, 21, 22, 23, 24, 25],
[30, 31, 32, 33, 34, 35],
[40, 41, 42, 43, 44, 45],
[50, 51, 52, 53, 54, 55]])
可以使用切片和整数索引的组合从这个二维数组中提取列和行:
In [64]: A[:, 1]
Out[64]: array([ 1, 11, 21, 31, 41, 51])
In [65]: A[1, :]
Out[65]: array([10, 11, 12, 13, 14, 15])
In [66]: A[:3, :3]
Out[66]:
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22]])
In [67]: A[::2, ::2]
Out[67]:
array([[ 0, 2, 4],
[20, 22, 24],
[40, 42, 44]])
In [69]: A[1::2, 1::3]
Out[69]:
array([[11, 14],
[31, 34],
[51, 54]])

三/向量化表达式
将数值数据存储在数组中的目的是为了能够使用简洁的向量化表达式来处理数据。向量化表达式的有效使用消除了许多使用显式 for 循环的必要。减少了冗长代码,具有更好的可维护性和更高的性能。
- 算术运算
In [43]: x = np.array([[1, 2], [3, 4]])
In [44]: y = np.array([[5, 6], [7, 8]])
In [45]: x + y
Out[45]:
array([[ 6, 8],
[10, 12]])
In [46]: x - y
Out[46]:
array([[-4, -4],
[-4, -4]])
In [47]: x * y
Out[47]:
array([[ 5, 12],
[21, 32]])
In [48]: y / x
Out[48]:
array([[5. , 3. ],
[2.33333333, 2. ]])
In [49]: x * 2
Out[49]:
array([[2, 4],
[6, 8]])
In [50]: 2 ** x
Out[50]:
array([[ 2, 4],
[ 8, 16]], dtype=int32)
In [51]: y / 2
Out[51]:
array([[2.5, 3. ],
[3.5, 4. ]])
In [52]: (y / 2).dtype
Out[52]: dtype('float64')
下表给出了 NumPy 数组算术运算操作符的汇总。这些运算符使用 Python 中的标准符号。

- 逐元素操作(element-wise)函数
NumPy 提供向量化函数,对许多基本数学函数和运算进行逐元素地评估。下表给出了 NumPy 中的基本数学函数的总结。这些函数都将单个数组(任意维)作为输入,在对应元素上应用相应的函数,并返回一个具有相同形状的新数组。输出数组的数据类型不一定与输入数组的数据类型相同。


In [72]: x = np.linspace(-1, 1, 11)
In [73]: x
Out[73]: array([-1. , -0.8, -0.6, -0.4, -0.2, 0. , 0.2, 0.4, 0.6, 0.8, 1. ])
In [74]: y = np.sin(np.pi * x)
In [75]: np.round(y, decimals=4)
Out[75]