数学之路-机器学习-机器学习算法-神经网络[11]
Posted 麦好
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学之路-机器学习-机器学习算法-神经网络[11]相关的知识,希望对你有一定的参考价值。
多层感知器的代码,需要一个比较复杂的调试过程,不过也有一些方法来加快这一速度,其中有几个地方要注意:
1、输入层、输出层、中间层的学习率和动量参数不能一样,
2、3个层的权值策略不能一样
输入层的权值的最好效果是能将相差较大的输入样本,输出成分布不能太接近饱和的输出
关于权值初始化的问题,可以考虑 Nguyen-Widrow algorithm,这也是matlab的权值矩阵初始化策略
采用tanh函数,要意识到,它的输出极限是[-a,+a]
3、在输出层外加上一个硬限幅层,保证输出为需要的结果
硬限幅层要灵活,不一定是下面这种形式
if v>=0:
return 1
else:
return 0
因为我们的输出值只有2个,所以可以暂时先设为这种形式,以后进行改进:
def o_func(myy):
myresult=[]
for i in xrange(0,len(myy)):
mean=np.mean(myy)
if myy[i]>mean:
myresult.append(1.0)
else:
myresult.append(0.0)
return np.array(myresult)
本博客所有内容是原创,未经书面许可,严禁任何形式的转载
http://blog.csdn.net/u010255642
最后,总结一下,多层感知器网络是门艺术,不能说是一个非常严谨的科学,带有随机性,虽然有梯度下降,动量调整的数学基础
下面是对下面这组输入 数据进行训练,最后对未知样本进行仿真
x = [[4,11],[7,340],[10,95],[3,29],[7,43],[5,128]]
d =[[1,0],[0,1],[1,0],[0,1],[1,0],[0,1]]
结果如下:
.......
......
-------开始第33次训练---------
-------开始第1个样本----------
前向计算中...
反向计算中...
-------开始第2个样本----------
前向计算中...
反向计算中...
-------开始第3个样本----------
前向计算中...
反向计算中...
-------开始第4个样本----------
前向计算中...
反向计算中...
-------开始第5个样本----------
前向计算中...
反向计算中...
-------开始第6个样本----------
前向计算中...
反向计算中...
训练成功,正在进行检验
仿真计算中
仿真计算中
仿真计算中
仿真计算中
仿真计算中
仿真计算中
训练成功,误差为:0.000000
样本:4===11 =>
仿真计算中
[ 1. 0.]
=====正确目标值=====
[1, 0]
样本:7===340 =>
仿真计算中
[ 0. 1.]
=====正确目标值=====
[0, 1]
样本:10===95 =>
仿真计算中
[ 1. 0.]
=====正确目标值=====
[1, 0]
样本:3===29 =>
仿真计算中
[ 0. 1.]
=====正确目标值=====
[0, 1]
样本:7===43 =>
仿真计算中
[ 1. 0.]
=====正确目标值=====
[1, 0]
样本:5===128 =>
仿真计算中
[ 0. 1.]
=====正确目标值=====
[0, 1]
测试值:9.000000===80.000000
仿真计算中
[ 1. 0.]
正确目标值:[1,0]
测试值:6.500000===272.000000
仿真计算中
[ 0. 1.]
正确目标值:[0,1]
>>>
同时因为输入数据五花八门,在训练之前要对数据进行预处理,通过预处理权值矩阵使其数值不能过大或过小,这样能较好得保证,
在随后的训练中通过S型非线性神经元,输出不会太接近极限
如下面输入的 数据分布
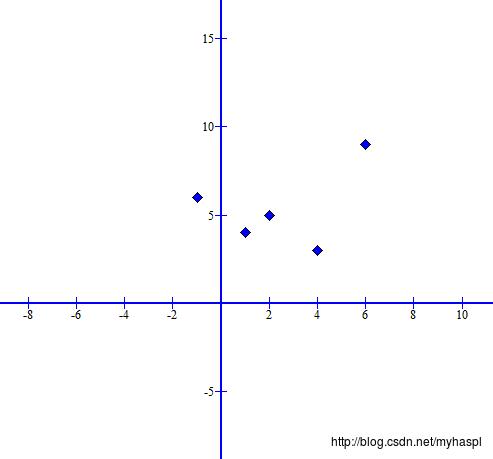
通过调整后转换成下面的均匀分布,将更有助于后面的训练
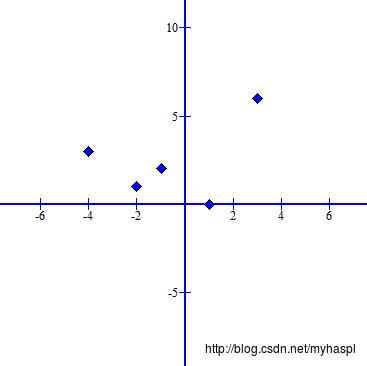
以上是关于数学之路-机器学习-机器学习算法-神经网络[11]的主要内容,如果未能解决你的问题,请参考以下文章