利用反向推理来解决“到达终点”问题

Posted 2022-04-14 &小小白&

七、到达终点

7.1、题设要求

​​  给定四个整数 sx , sy ，tx 和 ty，如果通过一系列的转换可以从起点 (sx, sy) 到达终点 (tx, ty)，则返回 true，否则返回 false。从点 (x, y) 可以转换到 (x, x+y) 或者 (x+y, y)。

示例 1:
输入: sx = 1, sy = 1, tx = 3, ty = 5
输出: true

解释:
可以通过以下一系列转换从起点转换到终点：
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)

示例 2:
输入: sx = 1, sy = 1, tx = 2, ty = 2 
输出: false

示例 3:
输入: sx = 1, sy = 1, tx = 1, ty = 1 
输出: true

提示:
1 <= sx, sy, tx, ty <= 109

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reaching-points

7.2、解题思路

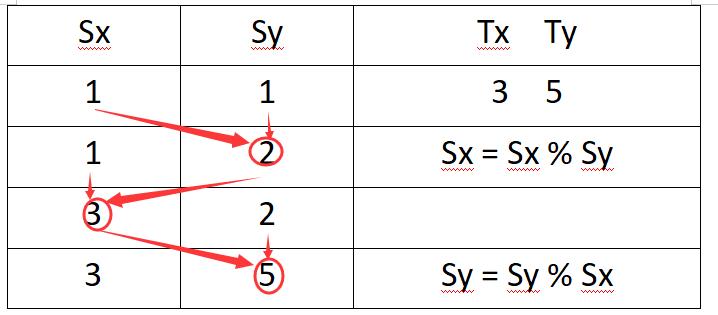
​​  此题使用反向推理操作，先将(tx,ty)进行反向操作，直到无法进行反向操作（最终将会推至(sx,sy)的下一个状态），就可以进行下一步操作，将上述结论推出的状态与(sx,sy)进行计算与判断，得出boolean值。

7.3、算法

class Solution 
    public boolean reachingPoints(int sx, int sy, int tx, int ty) 
        //将(tx,ty)进行反向操作，直到无法进行反向操作，就可以进行下一步
        //最终将会推至(sx,sy)的下一个状态
        while(tx > sx && ty > sy && tx != ty)
            if(tx > ty)
                //上一个状态为(tx - ty,ty)
                tx %= ty;
            else
                //上一个状态为(tx,ty - tx)
                ty %= tx;
        
        //将上述结论推出的状态与(sx,sy)进行计算与判断，得出boolean值
        if(tx == sx && ty == sy)
            //两组数均相对应的相等，故两数组相等
            return true;
        else if(tx == sx)
            return ty > sy && (ty - sy) % tx == 0;
        else if(ty == sy)
            return tx > sx && (tx - sx) % ty == 0;
        else
            return false;