弗洛伊德（Floyd）算法求图的最短路径

Posted 2022-04-13 JeffCoding

弗洛伊德基本思想

弗洛伊德算法作为求最短路径的经典算法，其算法实现相比迪杰斯特拉等算法是非常优雅的，可读性和理解都非常好。

基本思想：
弗洛伊德算法定义了两个二维矩阵：

1. 矩阵D记录顶点间的最小路径
   例如D[0][3]= 10，说明顶点0 到 3 的最短路径为10；
2. 矩阵P记录顶点间最小路径中的中转点
   例如P[0][3]= 1 说明，0 到 3的最短路径轨迹为：0 -> 1 -> 3。

它通过3重循环，k为中转点，v为起点，w为终点，循环比较D[v][w] 和 D[v][k] + D[k][w] 最小值，如果D[v][k] + D[k][w] 为更小值，则把D[v][k] + D[k][w] 覆盖保存在D[v][w]中。

概念是比较难理解的，我们来看图：

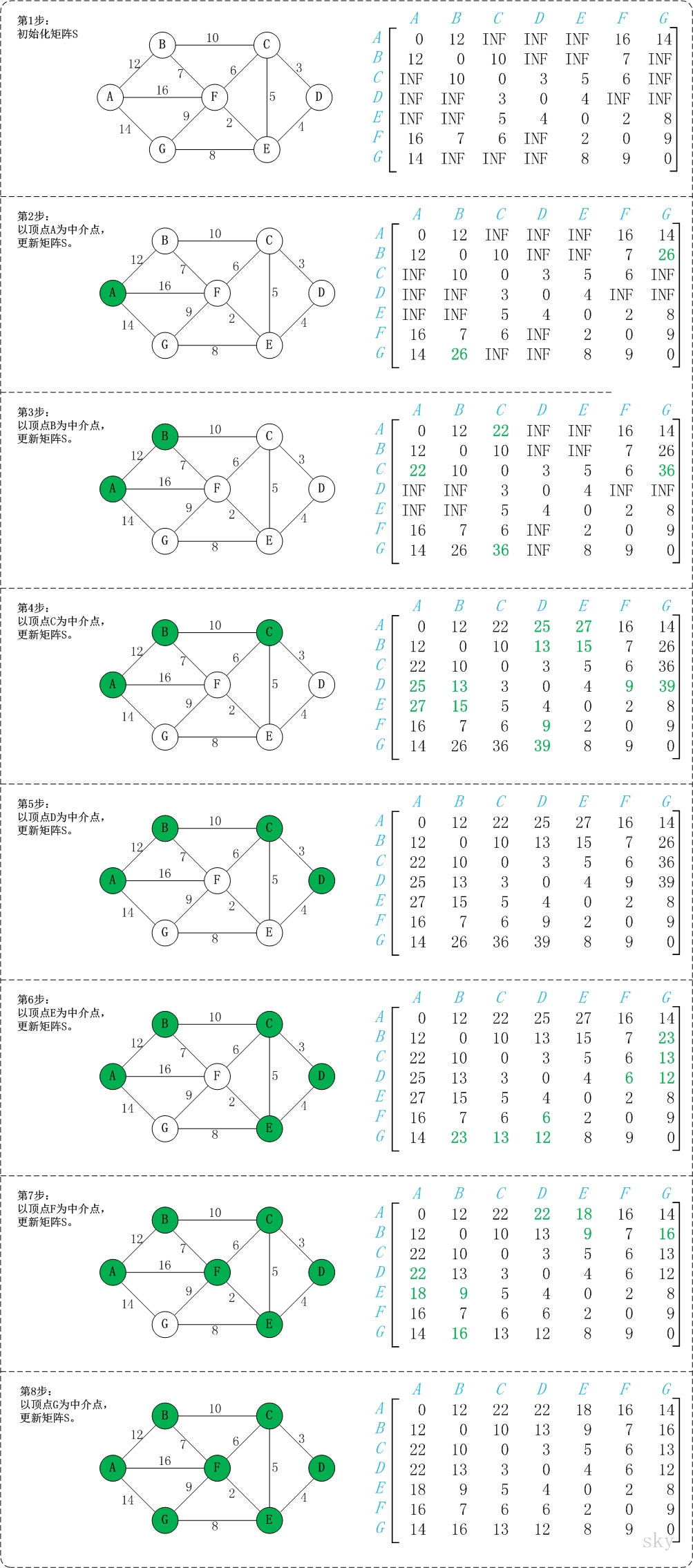
顶点名称和下标的对应
A B C D E F G
0 1 2 3 4 5 6

第2步：
以A为中间点，原D矩阵中，D[B][G]的值为INF，即不存在B->G的最小路径，但是通过A为中间点，D[B][A] + D[A][G] = 12 + 14 = 26 小于 D[B][G] = INF， 所以D[B][A] + D[A][G] 为 B -> G的最小值，因此覆盖D[B][G] 为 26。

第3步：
以B为中间点，第2步后的D矩阵中，D[A][C]的值为INF， 但是通过B，D[A][B] + D[B][C] = 12 + 10 = 22 小于 D[A][C] = INF，所以D[A][B] + D[B][C] 为 A->C的最小路径，覆盖D[A][C]的值为22， 以此类推。

第4步….

代码实现

我们就对上面的图进行弗洛伊德算法求最短路径，并且我们求A到D的最小路径，即v = 0， w = 3；

结构定义

typedef struct struct_graph
    char vexs[MAXN];
    int vexnum;//顶点数 
    int edgnum;//边数 
    int matirx[MAXN][MAXN];//邻接矩阵 
 Graph;

弗洛伊德算法

//这里是弗洛伊德算法的核心部分 
    //k为中间点 
    for(k = 0; k < G.vexnum; k++)
        //v为起点 
        for(v = 0 ; v < G.vexnum; v++)
            //w为终点 
            for(w =0; w < G.vexnum; w++)
                if(D[v][w] > (D[v][k] + D[k][w]))
                    D[v][w] = D[v][k] + D[k][w];//更新最小路径 
                    P[v][w] = P[v][k];//更新最小路径中间顶点 
                
            
        
    

求A 到 D的最短路径

    v = 0;
    w = 3;
    //求 0 到 3的最小路径
    printf("\\n%d -> %d 的最小路径为：%d\\n", v, w, D[v][w]);
    k = P[v][w];
    printf("path: %d", v);//打印起点
    while(k != w)
        printf("-> %d", k);//打印中间点
        k = P[k][w]; 
    
    printf("-> %d\\n", w);

完整代码

#include <stdio.h>
#include <stdlib.h>

#define MAXN 10 
#define INF = 1000

typedef struct struct_graph
    char vexs[MAXN];
    int vexnum;//顶点数 
    int edgnum;//边数 
    int matirx[MAXN][MAXN];//邻接矩阵 
 Graph;

int pathmatirx[MAXN][MAXN];//记录对应点的最小路径的前驱点，例如p(1,3) = 2 说明顶点1到顶点3的最小路径要经过2 
int shortPath[MAXN][MAXN];//记录顶点间的最小路径值

void short_path_floyd(Graph G, int P[MAXN][MAXN], int D[MAXN][MAXN])
    int v, w, k;
    //初始化floyd算法的两个矩阵 
    for(v = 0; v < G.vexnum; v++)
        for(w = 0; w < G.vexnum; w++)
            D[v][w] = G.matirx[v][w];
            P[v][w] = w;
        
    

    //这里是弗洛伊德算法的核心部分 
    //k为中间点 
    for(k = 0; k < G.vexnum; k++)
        //v为起点 
        for(v = 0 ; v < G.vexnum; v++)
            //w为终点 
            for(w =0; w < G.vexnum; w++)
                if(D[v][w] > (D[v][k] + D[k][w]))
                    D[v][w] = D[v][k] + D[k][w];//更新最小路径 
                    P[v][w] = P[v][k];//更新最小路径中间顶点 
                
            
        
    

    printf("\\n初始化的D矩阵\\n");
    for(v = 0; v < G.vexnum; v++)
        for(w = 0; w < G.vexnum; w++)
            printf("%d ", D[v][w]);
        
        printf("\\n");
    

    printf("\\n初始化的P矩阵\\n");
    for(v = 0; v < G.vexnum; v++)
        for(w = 0; w < G.vexnum; w++)
            printf("%d", P[v][w]);
        
        printf("\\n");
    

    v = 0;
    w = 3;
    //求 0 到 3的最小路径
    printf("\\n%d -> %d 的最小路径为：%d\\n", v, w, D[v][w]);
    k = P[v][w];
    printf("path: %d", v);//打印起点
    while(k != w)
        printf("-> %d", k);//打印中间点
        k = P[k][w]; 
    
    printf("-> %d\\n", w);


int main()
    int v, w;
    Graph G;
    printf("请输入顶点数:\\n");
    scanf("%d", &G.vexnum);
    printf("请输入初始矩阵值：\\n");
    for(v = 0; v < G.vexnum; v++)
        for(w = 0; w < G.vexnum; w++)
            scanf("%d", &G.matirx[v][w]);
        
    
    printf("\\n输入的矩阵值：\\n");
    for(v = 0; v < G.vexnum; v++)
        for(w = 0; w < G.vexnum; w++)
            printf("%d ", G.matirx[v][w]);
        
        printf("\\n");
    
    short_path_floyd(G, pathmatirx, shortPath);

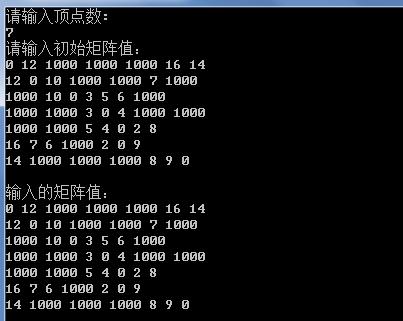
操作结果

初始化操作

弗洛伊德算法后的D矩阵和P矩阵

求得的最短路径