机器学习中的距离计算方法
Posted 小葵花幼儿园园长
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习中的距离计算方法相关的知识,希望对你有一定的参考价值。
机器学习中的距离计算方法?
在做很多研究问题时常常需要估算不同样本之间的相似性度量(
Similarity Measurement),这时通常采用的方法就是计算样本间的“距离”(Distance)。采用什么样的方法计算距离是很讲究,甚至关系到分类的正确与否。
1. 欧式距离
欧氏距离是一个通常采用的距离定义,指两个点之间的真实距离
二维:

三维:
n维:
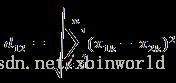
2. 曼哈顿距离
我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离,也就是:
- 在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
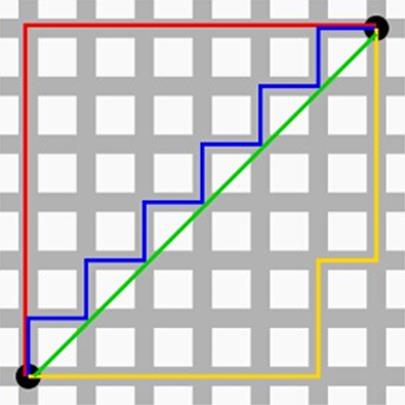
在平面上,坐标点(x1,y1)与坐标点(x2,y2)的曼哈顿距离为:
d
(
i
,
j
)
=
∣
x
1
−
x
2
∣
+
∣
y
1
−
y
2
∣
d(i,j)=|x_1 - x_2|+|y_1 - y_2|
d(i,j)=∣x1−x2∣+∣y1−y2∣
3.余弦距离
- 一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小
- 余弦值接近1,夹角趋于O,表明两个向量越相似
- 余弦值接近于0,夹角趋于90度,表明两个向量越不相似。
c o s = x 1 ∗ x 2 + y 1 ∗ y 2 x 1 2 + y 1 2 ∗ x 2 2 + y 2 ∗ 2 cos = \\fracx_1*x_2+y_1*y_2\\sqrtx_1^2+y_1^2* \\sqrtx_2^2+y_2*2 cos=x12+y12∗x22+y2∗2x1∗x2+y1∗y2
4.切比雪夫距离
切比雪夫距离是向量空间中的一种度量,二个点之间的距离定义是其各坐标数值差绝对值的最大值.
二维平面两点:
m
a
x
∣
x
1
−
x
2
∣
,
∣
y
1
−
y
2
∣
max\\|x_1-x_2|,|y_1-y_2|\\
max∣x1−x2∣,∣y1−y2∣
两个n维向量:
或者是
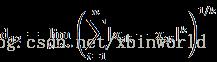
以上是关于机器学习中的距离计算方法的主要内容,如果未能解决你的问题,请参考以下文章