数学建模2018年全国大学生数学建模-热防护服的设计（附部分MATLAB代码）

Posted 2022-04-05 文宇肃然

蒙特卡罗方法简介

蒙特卡罗（Monte Carlo, abbr. MC）方法是利用独立重复的统计实验来对物理及数学问题求解的方法。一个简单的关于MC方法的应用即求解图形的面积。

完整代码详见

实战应用案例：热防护服的设计蒙特卡罗法求解热传导方程（MATLAB实现）

例：求解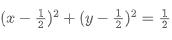的面积？

%投点次数
M = 1000;
A = rand(M,2);
r = sqrt((A(:,1) - 0.5).^2 + (A(:,2) - 0.5).^2);
total = sum(r < 0.5);
pr = total / M;
disp(pr)

%绘图
xt = @(t) 0.5*cos(t) +0.5;
yt = @(t) 0.5*sin(t) + 0.5;
fplot(xt,yt)
hold on
plot(A(:,1),A(:,2),\'.\');
grid on
axis equal
axis([0,1,0,1])

计算结果：0.7630