[数据结构读书笔记C++] 并查集详解
Posted 凌星An
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[数据结构读书笔记C++] 并查集详解相关的知识,希望对你有一定的参考价值。
介绍
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的 合并及查询 问题。
其主要操作为:
Union(合并) :将两个节点所在集合合并为一个集合
Find (查询) :查询某个节点属于哪个集合(即返回所在树的根节点)
图示:
通过上面的表述,恐怕我们并不清楚并查集到底是什么样子的?
下面我们用 图来表示一下
有四个节点我们编号为1,2,3,4,也可以有四棵树,每棵树只有一个节点,该节点即为根节点。这四棵树组成的集合(森林 就是我们所说的并查集

我们使用数组存储 ,上方所示即为
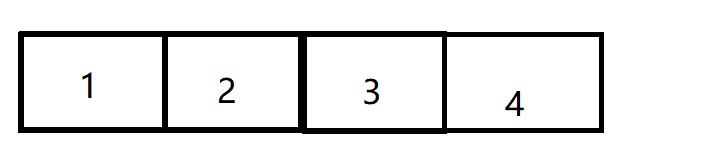
每个节点即为一个集合,每个集合的根节点为自己
合并: 所谓合并就是两棵树合并为一棵树,就是把上面两个节点联系在一起;比如我们合并1,2 两个节点,并且让2 为根节点(也可以1为根节点,这里以2为根节点示例)

经过合并之后,只有三个集合即三棵树 ,存储的数组变化为
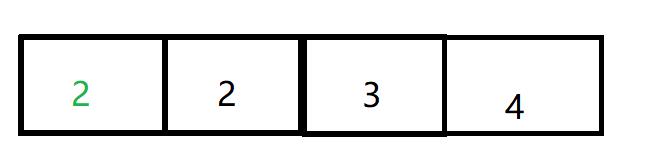
编号为1节点和编号为2的节点 为一个集合,且以2为根,故1号位置存储编号2
查询: 找到系欸但所在集合的根节点
以查询编号为1的节点为例:
我们在数组中找1号位置值为2 ,与编号不同
查找2号位置,值为2,与编号相同,所以编号为1的节点的根节点为2
代码实现
经过了上面的演示,相信大家对于并查集有了最基本的认识,下面我们进行代码实现。
并查集的基本实现
const int N ; //并查集中的节点个数
int p[N]; //存放节点所在树的根节点
void init()
//初始化,刚开始每个节点都是一棵树,根节点就是它自己
for(int i=1;i<=N;i++)
p[i]=i;
int Find(int x)
if(p[x]!=x)
//如果不相等,则根节点并非x , 那么去找p[x]的父节点
return find(p[x]);
return p[x];
void Union(int x,int y)
// 找到x,y所在树的根节点
int px=find(x),py=find(y);
//根节点不相同,则不是一棵树,进行合并
if(px!=py)
//合并后的根节点为py
p[px]=py;
代码优化
路径压缩
在并查集的操作当中,我们最常使用的是 Find 查询操作 。查询操作的复杂度决定了整体运行效率。
那么思考一下什么情况下,查询操作效率会很低呢?
思考一下树的高度很大的时候。
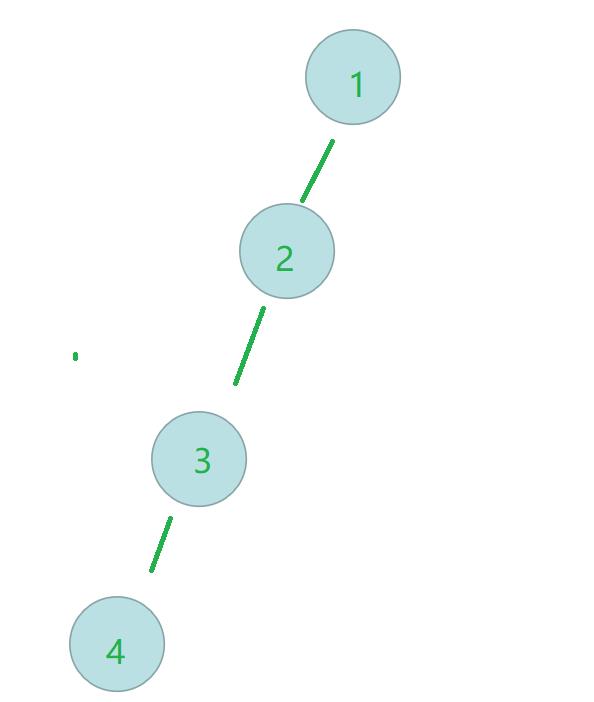
倘若我们查询4号节点,需要从4号节点往上进行查询,复杂度即为O(h),h为树的高度 ,倘若对于深处节点查询频繁的话,效率会很低。
因此,为了避免这种情况,出现了路径压缩的方式,其思想是将上面图片的树,改造为如下所示:
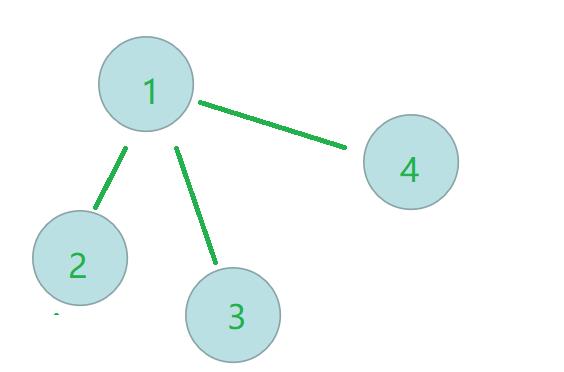
每个子节点的父节点即为根节点,查询操作复杂度O(1)即可
优化代码:
int Find(int x)
if(p[x]!=x)
//如果不相等,则向上查找;find函数返回的结果一定为根节点
// 查询结果赋值给p[x],设置当前节点x的父节点为根节点
p[x]=find(p[x]);
return p[x];
按秩合并
关于 秩 其实有两种解释 :一种是树的高度,另一种是树的节点个数(集合大小)我们这里采用的是 树 的高度。
按秩合并其实是一种启发式合并 即:把小的数据结构 合并到大的数据结构当中,并且只增加小的数据结构的 查询 代价 。
情况如图所示: 两个集合进行合并
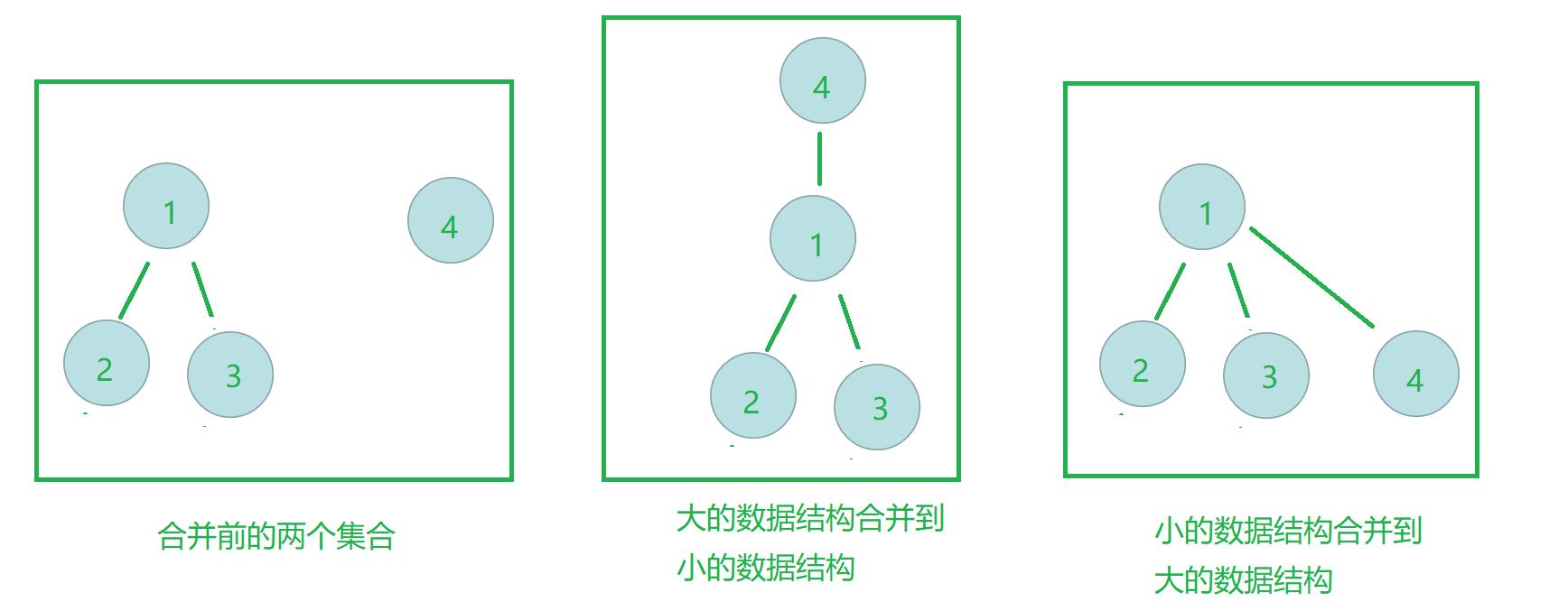
我们可以观察到最右边的图,合并后,进行查询,效率会更好,这种合并方式就是我们正在讨论的 按秩合并 。
优化代码
const int N ; //并查集中的节点个数
int p[N]; //存放节点所在树的根节点
int rank[N] ;//存放秩的数组,每个集合的秩进存放在根节点
void init()
//初始化,刚开始每个节点都是一棵树,根节点就是它自己
//每个节点的秩为1
for(int i=1;i<=N;i++)
p[i]=i;
rank[i]=1;
int Find(int x)
if(p[x]!=x)
//路径压缩 优化
p[x]= find(p[x]);
return p[x];
void Union(int x,int y)
// 找到x,y所在树的根节点
int px=find(x),py=find(y);
//根节点不相同,则不是一棵树,进行合并
if(px!=py)
// 按秩合并 优化
if(rank[px]<=rank[py])
p[px]=py;
//两个集合的秩相同,合并后的集合在原基础上加1
//原因如下图所示
rank[py]+=(rank[x]==rank[y]?1:0);
else
p[py]=px;

题目练习:
1250. 格子游戏
链接: https://www.acwing.com/problem/content/1252/
Alice和Bob玩了一个古老的游戏:首先画一个 n×n 的点阵(下图 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n 和 m。n表示点阵的大小,m 表示一共画了 m 条线。
以后 m 行,每行首先有两个数字 (x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 D,则是向下连一条边,如果是 R 就是向右连一条边。输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 m 步之后也没有结束,则输出一行“draw”。
数据范围
1≤n≤200 ,
1≤m≤24000
输入样例:
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
输出样例:
4
思路:
输入样例当中给了我们一个点,及其所画的方向 。其实根据这些信息,我们可以得到两个点的信息,那怎么判断是否形成封闭的圆呢?
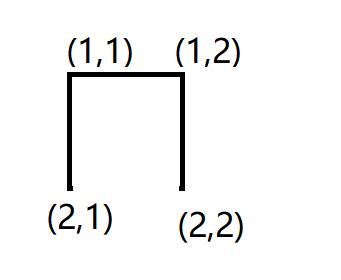
如图所示,我们只需要画一条线,线的两端为(2,1) (2,2) 即可以形成封闭的圆 。这种情况我们使用并查集是最为简单的,判断两个点是否在同一集合内,在的话可以形成封闭的圆。
代码:
#include<iostream>
#include<cstring>
using namespace std;
const int N=40000+10;
int p[N];
// 将二维坐标转换为唯一的数字表示
int get(int x,int y,int n)
x--,y--;
return x*n+y;
int find(int x)
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
int main()
int n=0,m=0;
cin>>n>>m;
//初始化
for(int i=0;i<n*n;i++)
p[i]=i;
for(int i=1;i<=m;i++)
int x=0,y=0;
char ch;
cin>>x>>y>>ch;
int a=get(x,y,n),b=0;
if(ch=='D')
b=get(x+1,y,n);
else if(ch=='R')
b=get(x,y+1,n);
int pa=find(a),pb=find(b);
if(pa==pb)
//如果在同意集合内,形成了封闭的圆,直接返回结果
printf("%d\\n",i);
return 0;
p[pa]=pb;
printf("draw\\n");
return 0;
1252. 搭配购买
链接:https://www.acwing.com/problem/content/1254/
Joe觉得云朵很美,决定去山上的商店买一些云朵。
商店里有 n 朵云,云朵被编号为 1,2,…,n,并且每朵云都有一个价值。
但是商店老板跟他说,一些云朵要搭配来买才好,所以买一朵云则与这朵云有搭配的云都要买。
但是Joe的钱有限,所以他希望买的价值越多越好。
输入格式
第 1 行包含三个整数 n,m,w,表示有 n 朵云,m 个搭配,Joe有 w 的钱。
第 2∼n+1行,每行两个整数 ci,di 表示 i 朵云的价钱和价值。
第 n+2∼n+1+m 行,每行两个整数 ui,vi,表示买 ui 就必须买 vi,同理,如果买 vi 就必须买 ui。
输出格式
一行,表示可以获得的最大价值。
数据范围
1≤n≤10000,
0≤m≤5000,
1≤w≤10000,
1≤ci≤5000,
1≤di≤100,
1≤ui,vi≤n
输入样例:
5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2
输出样例:
1
思路:
题目中给我们提供了一些物品的价格和价值;要求买u必须要买v,买v也必须买u ; 倘若买v还必须买w ,则u,v,w 可以认为是一个整体,要买一起买,不买则全部不买;如果把所有关联的物品全部看作一个整体,对于每个整体而言,只有买或者不买两种选择,求一定价钱内能买到物品的最大价值 即可转换为经典的01背包问题 。
而那些物品可以看作一个整体,则可使用并查集进行求取,根节点存储整个集合的价格和价值。
代码:
#include<iostream>
#include<cstring>
using namespace std;
const int N=10000+10;
int p[N];
int cost[N],value[N];
int find(int x)
if(p[x]!=x)
p[x]=find(p[x]);
return p[x];
int main()
int n=0,m=0,w=0;
scanf("%d%d%d",&n,&m,&w);
for(int i=0;i<n;i++)
p[i]=i;
for(int i=0;i<n;i++)
int c=0,d=0;
scanf("%d%d",&c,&d);
cost[i]=c,value[i]=d;
for(int i=0;i<m;i++)
int u=0,v=0;
scanf("%d%d",&u,&v);
u--,v--;
int pu=find(u),pv=find(v);
if(pu!=pv)
p[pu]=pv;
//根节点加上新加入节点对应的价格和价值
cost[pv]+=cost[pu];
value[pv]+=value[pu];
int dp[N];
memset(dp,0,sizeof dp);
for(int i=0;i<n;i++)
if(p[i]==i)
for(int j=w;j>=cost[i];j--)
dp[j]=max(dp[j],dp[j-cost[i]]+value[i]);
cout<<dp[w]<<endl;
return 0;
237. 程序自动分析
链接:https://www.acwing.com/problem/content/239/
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 x1,x2,x3,… 代表程序中出现的变量,给定 n 个形如 xi=xj 或 xi≠xj 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。
例如,一个问题中的约束条件为:x1=x2,x2=x3,x3=x4,x1≠x4,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式
输入文件的第 1 行包含 1 个正整数 t,表示需要判定的问题个数,注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第 1 行包含 1 个正整数 n,表示该问题中需要被满足的约束条件个数。
接下来 n 行,每行包括 3 个整数 i,j,e,描述 1 个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 e=1,则该约束条件为 xi=xj;若 e=0,则该约束条件为 xi≠xj。
输出格式
输出文件包括 t 行。
输出文件的第 k 行输出一个字符串 YES 或者 NO,YES 表示输入中的第 k 个问题判定为可以被满足,NO 表示不可被满足。
数据范围
1≤n≤10^5
1≤i,j≤10^9
输入样例:
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1
输出样例:
NO
YES
思路:
在这个题目当中,可以把输入分为两类,一类是相等的条件,另一类是不等的条件;倘若我们把相等的条件放在一遍,去看不等的条件,倘若不等的条件种两个变量出现在相等条件中,一定不被满足;倘若查询完毕后,没有出现刚才不满足情况,则一定是满足的。
把相等条件的变量全部放入并查集,查询不等的条件,倘若对应的两个变量在一个集合内部,则必不满足;不出现刚才必不满足的情况,则一定满足。
注: 数据量最大为 10^9 以此 来申请并查集的空间,则会超过题目给予的64MB大小;反观条件次数n为 10^6,则变量最多只有2 * 10^6 ,我们可以离散化处理,将大范围的变量处理到小范围上。
代码:
#include<iostream>
#include<cstring>
#include<vector>
#include<unordered_map>
using namespace std;
/*
注:数据量过大,需要进行离散化,将数据放在较小的定义域内
*/
const int N=2000010;
int p[N];
unordered_map<int,int> map;
int find(int x)
if(p[x]!=x)
p[x]=find(p[x]);
return p[x];
//离散化处理函数
int get(int x)
static int t=1;
if(map.count(x)==0)
map[x]=t++;
return map[x];
int main()
int t=0;
scanf("%d",&t);
while(t--)
for(int k=1;k<N;k++)
p[k]=k;
int n=0;
scanf("%d",&n);
vector<pair<int,int>> vec1;
vector<pair<int,int>> vec2;
for(int k=0;k<n;k++)
int i=0,j=0,e=0;
scanf("%d%d%d",&i,&j,&e);
if(e==0)
vec1.push_back(get(i),get(j));
else if(e==1)
vec2.push_back(get(i),get(j));
//处理相等的条件
for(int k=0;k<vec2.size();k++)
int i=vec2[k].first,j=vec2[k].second;
int pi=find(i),pj=find(j);
if(pi!=pj)
p[pi]=pj;
//遍历不等的条件,继续判断
int flag=true;
for(int k=0;k<vec1.size();k++)
int i=vec1[k].first,j=vec1[k].second;
int pi=find(i),pj=find(j);
if(pi==pj)
flag=false;
break;
if(flag)
puts("YES");
else
puts("NO");
return 0;
238. 银河英雄传说
链接: https://www.acwing.com/problem/content/240/
有一个划分为 N 列的星际战场,各列依次编号为 1,2,…,N。
有 N 艘战舰,也依次编号为 1,2,…,N,其中第 i 号战舰处于第 i 列。
有 T 条指令,每条指令格式为以下两种之一:
M i j,表示让第 i 号战舰所在列的全部战舰保持原有顺序,接在第 j 号战舰所在列的尾部。
C i j,表示询问第 i 号战舰与第 j 号战舰当前是否处于同一列中,如果在同一列中,它们之间间隔了多少艘战舰。
现在需要你编写一个程序,处理一系列的指令。
输入格式
第一行包含整数 T,表示共有 T 条指令。
接下来 T 行,每行一个指令,指令有两种形式:M i j 或 C i j。
其中 M 和 C 为大写字母表示指令类型,i 和 j 为整数,表示指令涉及的战舰编号。
输出格式
你的程序应当依次对输入的每一条指令进行分析和处理:
如果是 M i j 形式,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息;
如果是 C i j 形式,你的程序要输出一行,仅包含一个整数,表示在同一列上,第 i 号战舰与第 j 号战舰之间布置的战舰数目,如果第 i 号战舰与第 j 号战舰当前不在同一列上,则输出 −1。
数据范围
N≤30000,T≤500000
输入样例:
4
M 2 3
C 1 2
M 2 4
C 4 2
输出样例:
-1
1
思路:
对于判断是否是同一列,我们可以使用并查集,通过判断是否属于同一个结合来进行判断。
如果属于同一列(即同一集合),还需要输出之间的距离是多少,这个需要怎么处理呢?
倘若我们有一个数组d[ ] 记录并查集中每个节点到它所属集合的根节点的距离。根节点,我们设置为每列的第一个战舰。
则 对于两艘战舰x,y (x在y前面)而言,他们的距离为 d[y]-d[x]-1 则可以直接得到结果。
因此,我们只需要维护一个数组d[ ] ;
而维护d[ ] 主要在集合合并的时候,进行更新,那怎么更新呢?
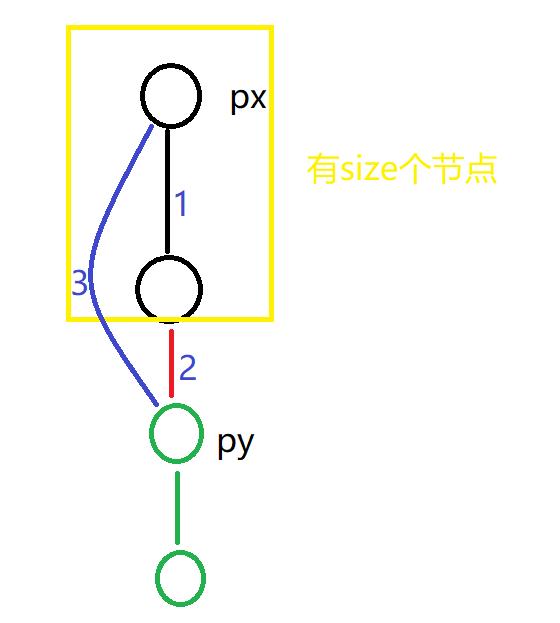
对于py集合而言,每个节点到根节点的距离只需要加上 3 的长度即可
而3的长度 ,如图所示为2 + 1的结果,线段2的长度为1 ,而线段1的长度为整个px集合节点个数
因此,还需要维护一个数组 Size [ ] 存放每个集合的节点数目
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
const