LeetCode算法技巧汇总 -- 持续更新，学无止境！

Posted 木兮同学

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode算法技巧汇总 -- 持续更新，学无止境！相关的知识，希望对你有一定的参考价值。

此篇是本人 LeetCode 算法刷题技巧总结，还包括刷过的算法题分类，自己记录以便后续二刷三刷，也分享给大家欢迎一起交流探讨。话说现在非常遗憾大学期间没能坚持搞 ACM，出来社会才越发觉得后悔，但是遗憾归遗憾，我还是相信种一棵树是十年前，其次是现在，所以重新再来为时不晚！刷起！！！

文章目录

一、数组、链表、跳表

二、栈、队列、树

三、递归、分治、回溯、DFS、BFS

四、贪心算法

五、二分查找

六、动态规划

七、字典树

  • 小技巧

    • 字典树，即 Trie 树，又称单词查找树或键树，是一种树形结构（每个父节点最多只有26个子节点）。典型的应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。
    • 优点是最大限度的减少无谓的字符串比较，查询效率比哈希高。
    • 核心代码：
      class Trie 

    private Trie[] children;
    private final Integer R = 26;
    private boolean end;

    Trie() 
        children = new Trie[R];
    

    public void insert(String word) 
        Trie node = this;
        for (int i = 0; i < word.length(); i++) 
            char c = word.charAt(i);
            int index = c - 'a';
            if (node.children[index] == null) 
                node.children[index] = new Trie();
            
            node = node.children[index];
        
        node.end = true;
    

    public boolean search(String word) 
        Trie node = this.searchWith(word);
        return node != null && node.end;
    

    public boolean startsWith(String word) 
        Trie node = this.searchWith(word);
        return node != null;
    

    private Trie searchWith(String word) 
        Trie node = this;
        for (int i = 0; i < word.length(); i++) 
            char c = word.charAt(i);
            int index = c - 'a';
            if (node.children[index] != null) 
                node = node.children[index];
             else 
                return null;
            
        
        return node;

  • 实战

八、并查集

  • 小技巧

    • 适用场景：组团、配对问题
    • 核心代码：
      private class UnionFind 
    /**
     * 连通分量的个数
     */
    private int count;
    private int[] parent;

    public int getCount() 
        return count;
    

	/*
	 * 一开始各个节点都是指向自己
	 */
    public UnionFind(int n) 
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) 
            parent[i] = i;
        
    

	/*
	 * 查询根节点
	 */
    private int find(int x) 
        while (x != parent[x]) 
            parent[x] = parent[parent[x]];
            x = parent[x];
        
        return x;
    

	/*
	 * 合并节点
	 */
    public void union(int x, int y) 
        int xRoot = find(x);
        int yRoot = find(y);
        if (xRoot == yRoot) 
            return;
        

        parent[xRoot] = yRoot;
        count--;

  • 实战

九、AVL树、红黑树

  • AVL树
    • 即平衡二叉树，任何节点左右子树高度差不超过 1，通过旋转来进行平衡
      • 左旋
      • 右旋
      • 左右旋
      • 右左旋
  • 红黑树
    • 是近似平衡的二叉搜索树，任何节点左右子树高度差小于 2 倍。它满足以下条件：
      • 每个节点要么是红色要么是黑色
      • 根节点是黑色
      • 每个叶子节点是黑色
      • 不能有相邻的两个红色节点
      • 从任一节点到每个叶子节点的路径都包含相同数目的黑色节点。

十、位运算

判断m是否是奇数：(m & 1) == 1 // 奇数，或者除2余数不为0：m % 2 != 0
x除以2：x >> 1 // mid = (left + right) / 2 --> mid = (left + right) >> 1
清零x最低位的1：x = x & (x - 1) // 10010 -> 10000 、0001000 -> 0000000
得到x最低位为1的x：x = x & -x
将x最右边的n位清零：x & (~0 << n)
获取x的第n位值：(x >> n) & 1
获取x的第n位的幂值：x & (1 << (n-1))
将第n位设为1：x | (1 << n)
将第n位设为0：x & (~(1 << n))
将x最高位至第n位（含）清零：x & ((1 << n) - 1)
将第n位至第0位（含）清零：x & (~((1 << (n + 1))-1))

十一、布隆过滤器、LRU 缓存

  • 布隆过滤器
    • 一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。
    • 优点：空间效率和查询效率都远远超过一般的算法。
    • 缺点：有一定的误识别率（能确定“一定不在”，但不能确定“一定在”）和删除困难。
    • 例如下图，能确定 C 一定不是目标元素，但不确定 A 和 B 是目标元素，虽然都在布隆过滤器能找到，但是实际上 B 并非目标元素。
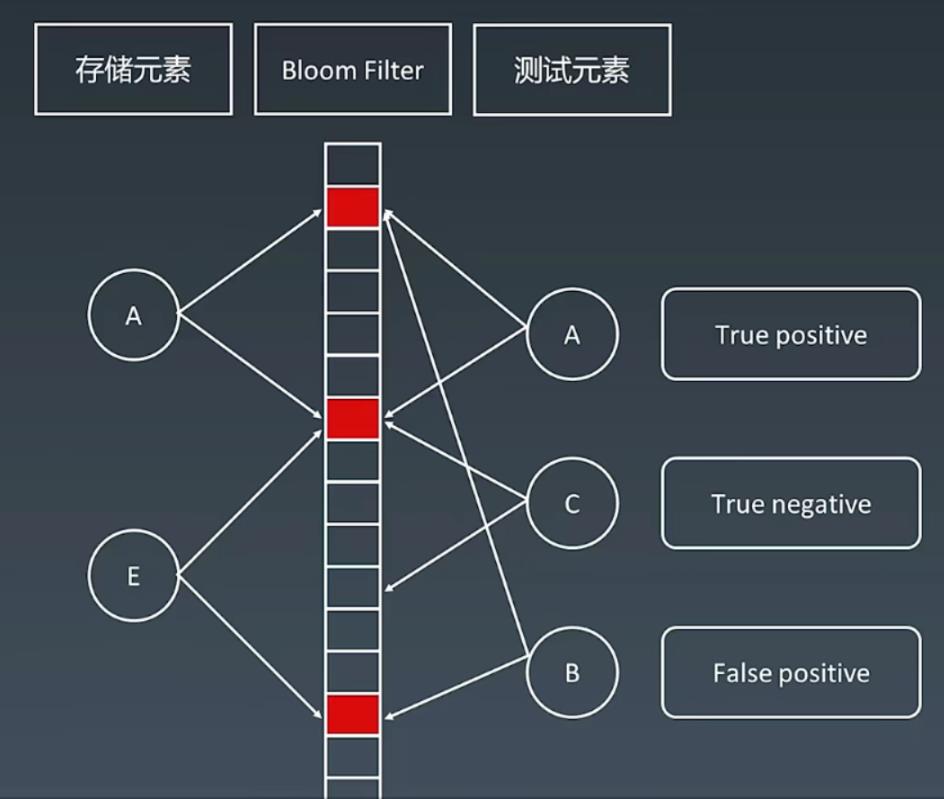
  • LRU 缓存
    • 全称：least recently used，即最少最近使用到的。
    • LFU：least frequently used，最近最不常用置换算法。
  • 实战

十二、排序算法

  • 十大排序算法，详情请点击 这里 。

十三、算法常用库函数小技巧（Java版）

数组排序：Arrays.sort(nums) // 对nums数组排序
数组填充：Arrays.fill(chars, '-') // 将chars数组全部填充为"-"
数组Copy：Arrays.copyOfRange(chars, 0, 10) // 复制chars中0（包含）-10（不包含）位为一个新数组
翻转字符串：new StringBuilder(strTmp).reverse().toString() // 将strTmp字符串翻转
拼接字符串：String.join(".", tmp) // 用"."拼接tmp（Iterable子类）中的数据为一个串
字符型数字转成Integer数字：减字符0 // 例如'5' - '0' 会等于 5
未完待续...

以上是关于LeetCode算法技巧汇总 -- 持续更新，学无止境！的主要内容，如果未能解决你的问题，请参考以下文章

leetcode算法228.汇总区间

LeetCode题解分类汇总（包括剑指Offer和程序员面试金典，持续更新）

Android常用技巧汇总(持续更新)

python使用小技巧汇总（持续更新）

LeetCode Animation 题目图解汇总(持续更新中...)

IDEA 常用的小技巧汇总，JAVA 新手上路必备，快上车！(持续更新)