信号与系统 2022 春季学期第五次作业
Posted 卓晴
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了信号与系统 2022 春季学期第五次作业相关的知识，希望对你有一定的参考价值。
◎ 本文网络下载链接： 2022年春季第第五次作业 : https://zhuoqing.blog.csdn.net/article/details/123712642
关于提交作业的基本要求，请参见： 通过提交两份作业综述对提交作业的基本要求 。
§01 基础作业
1.1 傅里叶级数分解
1.1.1 计算傅里叶级数并画出频谱
（1）题目内容
计算下面各图所示的周期信号的傅里叶级数分解系数，并绘制出频谱图。要求：
- 写出三角函数形式傅里叶级数分解系数，包括 a n , b n , c n , θ n a_n ,b_n ,c_n ,\\theta _n an,bn,cn,θn， n ≥ 0 n \\ge 0 n≥0 。
- 写出复指数形式傅里叶级数分解系数， F n , − ∞ < n < + ∞ F_n , - \\infty < n < + \\infty Fn,−∞<n<+∞ 。
- 绘制出双边频谱（幅度谱： ∣ F n ∣ \\left| F_n \\right| ∣Fn∣ ， 相位谱： θ n \\theta _n θn ）
▲ 图1.1.1 第一小题
▲ 图1.1.2 第二小题
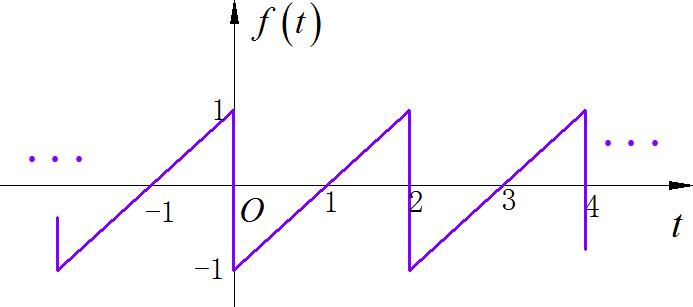
▲ 图1.1.3 第三小题
▲ 图1.1.4 第四小题
▲ 图1.1.5 第五小题
（2）题目要求
-
选做与必做：
-
必做题目：1、2、4
选做题：3、5
1.1.2 分析周期信号频谱
已知周期信号的傅里叶级数表达式为：
f
(
t
)
=
2
+
3
cos
2
t
+
4
sin
2
t
+
2
sin
(
3
t
+
3
0
o
)
−
cos
(
5
t
+
12
0
o
)
f\\left( t \\right) = 2 + 3\\cos 2t + 4\\sin 2t + 2\\sin \\left( 3t + 30^o \\right) - \\cos \\left( 5t + 120^o \\right)
f(t)=2+3cos2t+4sin2t+2sin(3t+30o)−cos(5t+120o)
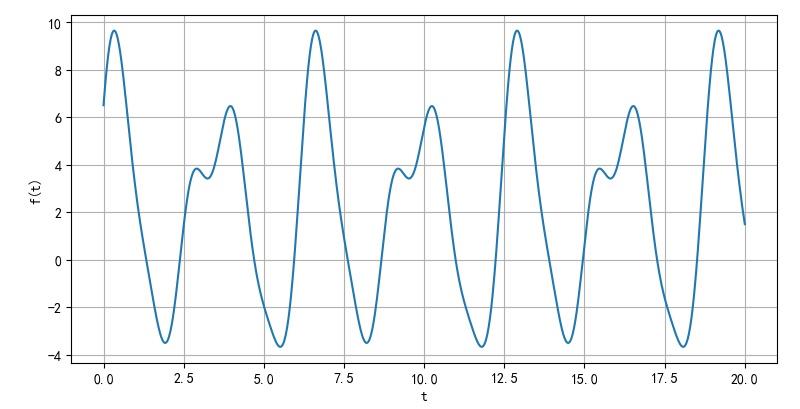
▲ 图1.1.6 f(t)信号波形
（1） 求
f
(
t
)
f\\left( t \\right)
f(t) 的基频；
（2） 绘制出
f
(
t
)
f\\left( t \\right)
f(t) 的幅度谱和相位谱；
注：
第一问需要根据已知信号中各个谢波德频谱找到该信号的主频率，也就是基波频率。它应该是信号中除了直流分量之外，其它各个交流分量周期（频谱）的最大公约数（最小公倍数）。
第二问要求绘制出幅度谱和相位谱。要求将信号表示为 c n cos ( n ω 1 t + θ n ) c_n \\cos \\left( n\\omega _1 t + \\theta _n \\right) cncos(nω1t+θn) 的形式，其中 c n c_n cn 需要大于等于0. θ n \\theta _n θn 取值在 [ − 18 0 o , 18 0 o ] \\left[ - 180^o ,180^o \\right] [−180o,180o] 之间的值。
1.2 傅里叶级数分解对称性
1.2.1 信号中的谐波分量
（1）必做题
已知周期电压信号
f
(
t
)
f\\left( t \\right)
f(t) 的波形如下图所示。其中
τ
=
5
μ
s
\\tau = 5\\mu s
τ=5μs ，
T
=
10
μ
s
T = 10\\mu s
T=10μs 。请问改矩形脉冲电压信号中是否存在如下的频率分量？
100
k
H
z
,
200
k
H
z
,
250
k
H
z
,
300
k
H
z
,
400
k
H
z
100kHz,\\,\\,200kHz,\\,\\,250kHz,\\,\\,300kHz,\\,\\,400kHz
100kHz,200kHz,250kHz,300kHz,400kHz
▲ 图1.2.1 电压信号波形
（2）选做题
请问，上述周期方波电压信号通过如下三个电路，哪些电路输出信号中存在 200 k H z 200kHz 200kHz 的频率分量？
▲ 图1.2.2 电路（1）
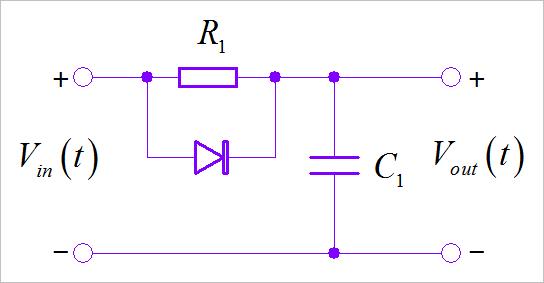
▲ 图1.2.3 电路（2）
▲ 图1.2.4 电路（3）
注：单稳态电路在每次触发后，输出时间为 1 μ s 1\\mu s 1μs 的高电平脉冲。
1.2.2 补齐周期信号
已知周期信号 f ( t ) f\\left( t \\right) f(t) 在其四分之一周期内的信号波形如下图所处：
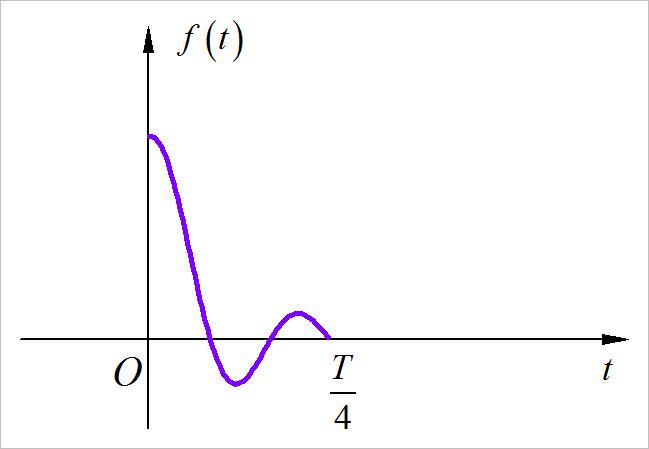
▲ 图1.2.5 周期信号中四分之一周期的波形
下面给出了该信号四种可能的存在的谐波分量。针对每一种情况分别绘制出改信号的一个周期内的完整波形。
（1） 信号为偶函数，只包含奇次谐波；
（2） 信号为奇函数，只包含偶次谐波；
（3） 信号为奇函数，只包含奇次谐波；
（4） 信号为偶函数，只包含偶次谐波；
1.2.3 判断信号中频率成分
（1）必做题
利用信号的对称性，确定下面个信号的傅里叶级数所含有的频率成分：
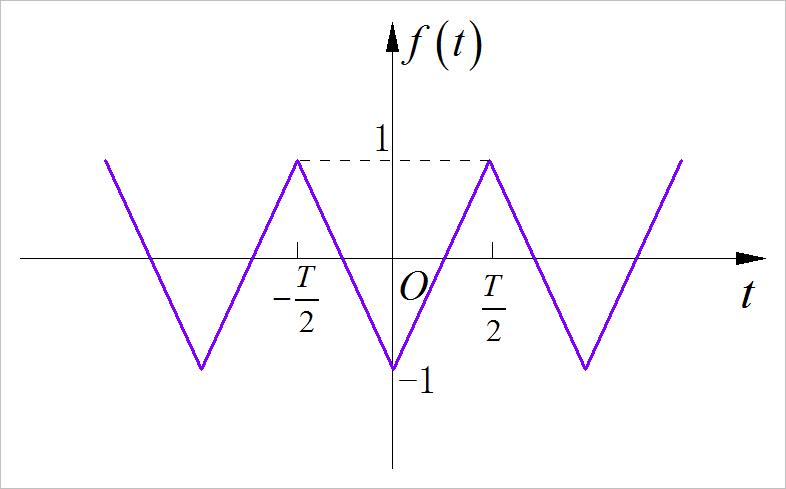
▲ 图1.2.6 第一小题
▲ 图1.2.7 第二小题
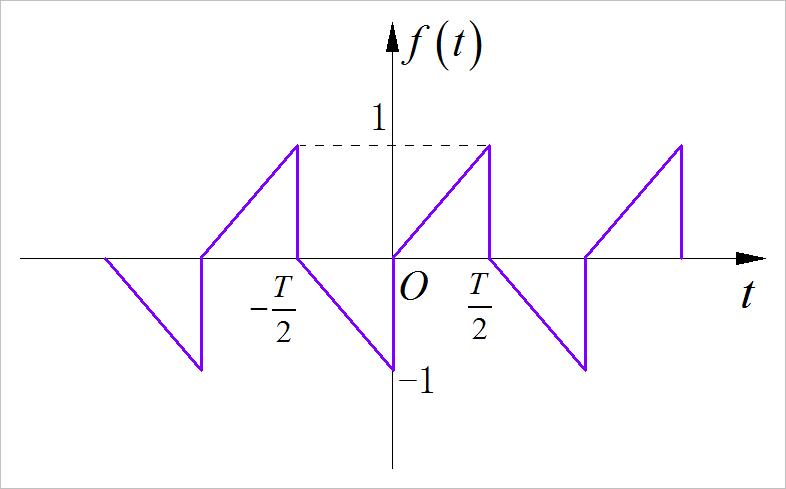
▲ 图1.2.8 第三小题
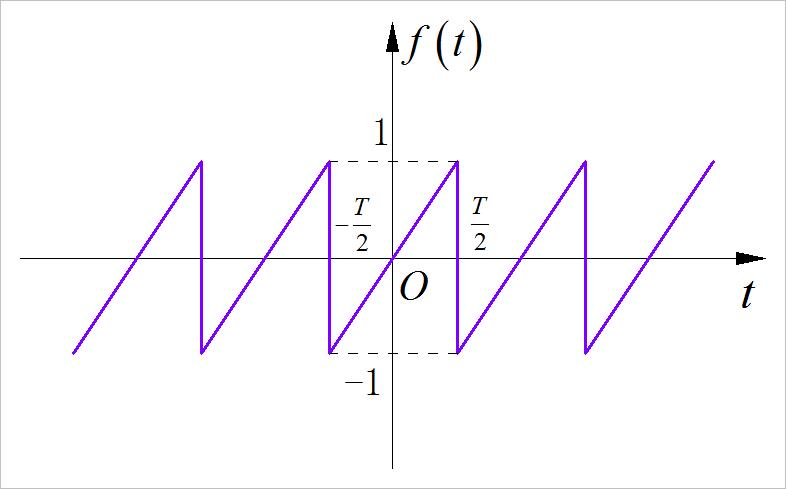
▲ 图1.2.9 第四小题
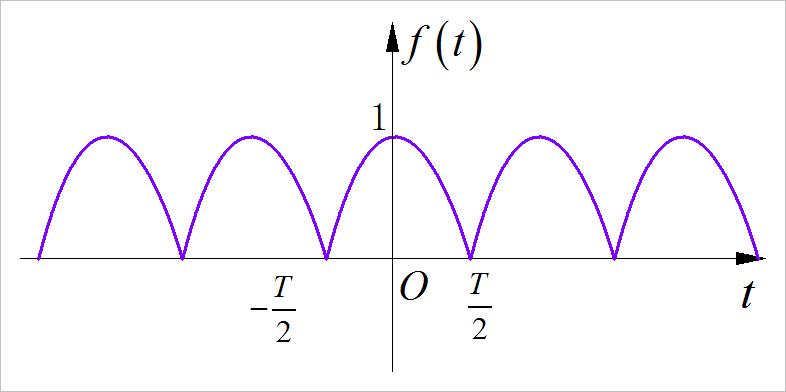
▲ 图1.2.10 第五小题
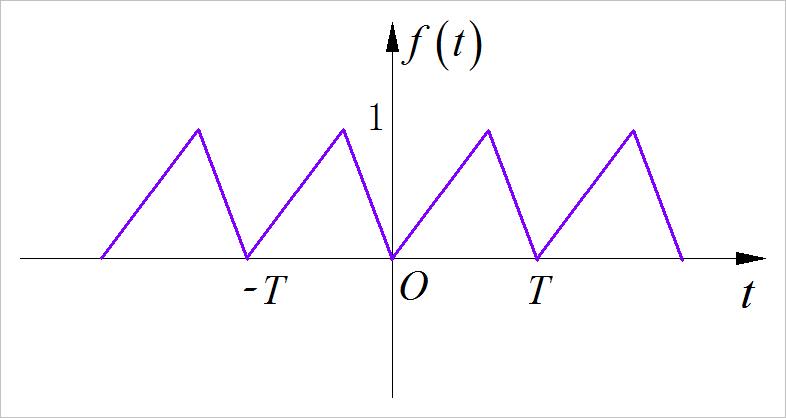
▲ 图1.2.11 第六小题
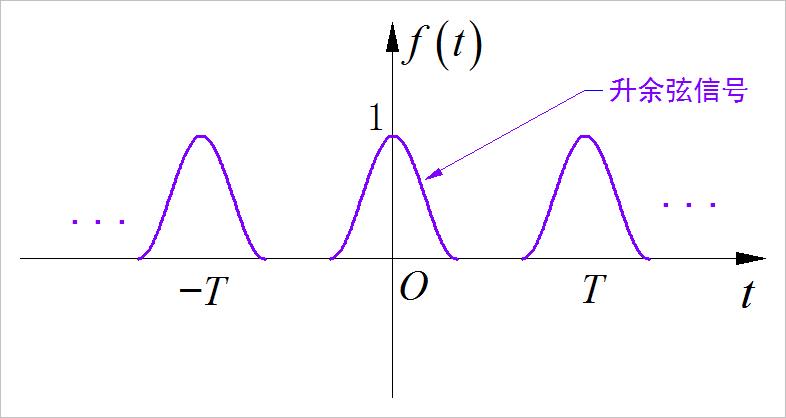
▲ 图1.2.12 第七小题
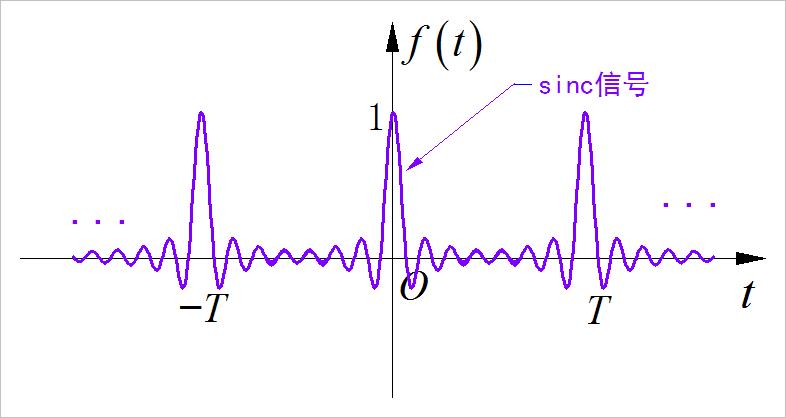
▲ 图1.2.13 第八小题
（2）选做题
请根据信号波形的光滑性，判断上述信号谐波衰减规律，即谐波幅值随着 n n n 增加而衰减的大致规律。
1.3 傅里叶级数分解性质
1.3.1 傅里叶级数分解微分特性
设 f ( t ) f\\left( t \\right) f(t) 为 [ − π , π ] \\left[ - \\pi ,\\pi \\right] [−π,π] 上的光滑函数，满足： f ( − π ) = f ( π ) f\\left( - \\pi \\right) = f\\left( \\pi \\right) f(−π)=f(π) 且 a n , b n a_n ,b_n an,bn 为 f ( t ) f\\left( t \\right) f(t) 的傅里叶级数系数。 a n ′ , b n ′ a'_n ,b'_n an′,以上是关于信号与系统 2022 春季学期第五次作业的主要内容，如果未能解决你的问题，请参考以下文章
2021年春季学期-信号与系统-第十五次作业参考答案-第二小题参考答案
2021年春季学期-信号与系统-第十五次作业参考答案-第五小题参考答案