全列举二叉搜索树 - 以太祖长拳打飞江湖第一流高手

Posted 2022-03-21 程序员超时空

全列举二叉搜索树 - 一个有意思的问题

给定一个正整数n，返回所有的二叉搜索树，每棵二叉搜索树都包含了 1-n 这n个数字。

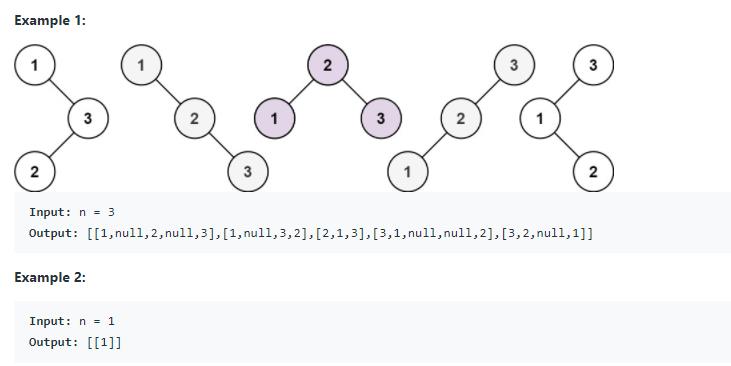
这题一看，比较容易这么想： 给定1-n个数字，先构造出一棵二叉搜索树； 然后再想办法推广这个方法，列举出所有的二叉搜索树。
这是一个简单直接的想法，程序员们往往也很乐意先去思考如何利用 1-n 构造出一棵二叉搜索树。
然而，根据笔者尝试的经验，这么做很费力，而且到最后不仅代码复杂，还很可能遇到设计上难以解决的问题。
因此，这种想法应该就是一个坑了； 它会误导程序员在错误递归的道路上走远，虽然最后可能会发现这原来是个坑。

如果碰壁过，那么会意识到，这里似乎不应该去递归地构造一棵树。
于是重新审题 - “返回所有的二叉搜索树” - 注意，这里返回的是一个集合，集合中的每个元素是一棵树。
于是进一步想到，是否能递归产生所有的左子树和所有的右子树呢？
如果能的话，那么拿到所有左子树和所有右子树之后，能做什么呢？
第二个问题很好回答，当拿到所有左子树和所有右子树之后， 2重for循环自然就列举出了所有的二叉搜索树。
问题是第一个问题，是否能递归产生所有的左子树和所有的右子树呢？ 试着写写代码，发现其实递归还是满好写的。

这里最大的一个坎，就是需要想到“递归产生所有的子树”。
因为这一点比较地反常识。常识是，递归操作一棵树，而这里是递归产生一个集合的树。属于一种更高层次的递归。
直觉上会觉得似乎太复杂，于是潜意识里很可能都没有了尝试的意愿。
但是，这里有2个lessons to learn：

• 递归不用在乎复杂度，直接去尝试就好。
• 一棵树看起来复杂，但其实会简化为一个root节点；（之后对root的递归，属于低层次递归，比如打印）

那么，究竟是如何用“递归去产生一个树林”呢？
首先要给定树林的范围，比如 1-n, 可泛化为 [beg, end ]
然后是递归的退出条件：

• beg > end : 这是不可能的情况，可直接退出 （但实际写程序的时候，会发现这里需要返回的一个只包含了一个 nullptr 的数组)
• beg = end : 这表示只需要为一个数字产生一个树林，于是直接返回一个只有一个元素的数组即可
• beg < end : 这是比较普遍的情况，此时最终产生的树林是 [beg, end] 里每个元素为root时的所有树，于是递归在此处发生

下面是基本数据结构和核心代码。真正的核心代码只有30行左右。

struct TreeNode 
    int val;
    TreeNode * left;
    TreeNode * right;
    TreeNode() : val(0), left(nullptr), right(nullptr) 
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) 
;

vector<TreeNode *> _genTreesBasedOnNums(int beg, int end) 
    vector<TreeNode *> trees;
    
    // Not possible, add nullptr to tree
    if(beg > end) 
        trees.push_back(nullptr);
        return trees;
    
    // Only one element in the subtree, so just add it
    if(beg == end) 
        trees.push_back(new TreeNode(beg));
        return trees;
    
    
    for(int i=beg; i<=end; i++) 
        // Each element in the 2 vectors stands for one Tree 
        vector<TreeNode *> leftTrees  = _genTreesBasedOnNums(beg, i-1);
        vector<TreeNode *> rightTrees = _genTreesBasedOnNums(i+1, end);
        
        for(int j=0; j<leftTrees.size(); j++) 
            for(int k=0; k<rightTrees.size(); k++) 
                TreeNode * root = new TreeNode(i);
                root->left = leftTrees[j];
                root->right = rightTrees[k];
                trees.push_back(root);
            
        
    
    return trees;


vector<TreeNode *> generateTrees(int n) 
    return _genTreesBasedOnNums(1, n);

下面再给出一个完整版（含测试）的代码。里面还会有一些打印的技巧。

#include <vector>
#include <queue>
#include <iostream>
using namespace std;

#define NO_NODE_VAL_NUM -9999

struct TreeNode 
    int val;
    TreeNode * left;
    TreeNode * right;
    TreeNode() : val(0), left(nullptr), right(nullptr) 
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) 
;


void layered_print_tree(TreeNode * root) 
    if (root == nullptr) return;
    
    vector<int> result;
    
    queue<TreeNode *> nodeQueue;
    nodeQueue.push(root);
    
    while (!nodeQueue.empty()) 
        TreeNode * tmp = nodeQueue.front();
        nodeQueue.pop();
        
        if (tmp == nullptr) 
            result.push_back(NO_NODE_VAL_NUM);
        
        else 
            result.push_back(tmp->val);
            
            if (tmp->left == nullptr && tmp->right == nullptr) continue; 
            
            nodeQueue.push(tmp->left);
            nodeQueue.push(tmp->right);
        
    
    
    while (!result.empty() and result.back() == NO_NODE_VAL_NUM) 
        result.pop_back();
    
    
    cout << "[";
    
    for(int i=0; i<result.size(); i++) 
        if (result[i] != NO_NODE_VAL_NUM) cout << result[i];
        else cout << "null"; 
        if (i != result.size()-1 ) cout << ", "; 
    
    
    cout << "]";


void print_trees(const vector<TreeNode *> & vec) 
    cout << "There are " << vec.size() << " trees generated" << endl;
    
    cout << "["; 
    for (int i=0; i<vec.size(); i++) 
        layered_print_tree(vec[i]);
        if (i < vec.size()-1) cout << ", ";
    
    cout << "]" << endl;


void destruct_tree(TreeNode * root) 
    if (root == nullptr) return;
    destruct_tree(root->left);
    destruct_tree(root->right);
    delete root;


//
// This function generates trees based on the given consequencial numbers
// 
// Parameters:
//      int beg       the begin number 
//      int end       the end number 
// Return:
//      A vector of TreeNode *
//      Each element is one tree's root 
//      Each tree contains all the numbers from beg to end 
//      Each number in [beg, end] could be root 
//
vector<TreeNode *> _genTreesBasedOnNums(int beg, int end) 
    vector<TreeNode *> trees;
    
    // Not possible, add nullptr to tree
    if(beg > end) 
        trees.push_back(nullptr);
        return trees;
    
    // Only one element in the subtree, so just add it
    if(beg == end) 
        trees.push_back(new TreeNode(beg));
        return trees;
    
    
    for(int i=beg; i<=end; i++) 
        // Each element in the 2 vectors stands for one Tree 
        vector<TreeNode *> leftTrees  = _genTreesBasedOnNums(beg, i-1);
        vector<TreeNode *> rightTrees = _genTreesBasedOnNums(i+1, end);
        
        for(int j=0; j<leftTrees.size(); j++) 
            for(int k=0; k<rightTrees.size(); k++) 
                TreeNode * root = new TreeNode(i);
                root->left = leftTrees[j];
                root->right = rightTrees[k];
                trees.push_back(root);
            
        
    
    return trees;


vector<TreeNode *> generateTrees(int n) 
    return _genTreesBasedOnNums(1, n);



int main()

    vector<TreeNode *> trees = generateTrees(3);
    print_trees(trees);
    
    for (auto & pTreeNode : trees) 
        destruct_tree(pTreeNode);
    
    
    return 0;

运行效果如下：

$ ./a.exe
There are 5 trees generated
[[1, null, 2, null, 3], [1, null, 3, 2], [2, 1, 3], [3, 1, null, null, 2], [3, 2, null, 1]]

本题的解法还是有点惊艳的。
普普通通的一套太祖长拳，直接打飞了江湖第一流的高手。
太祖长拳的取胜，在于更深的内力与从容的法度；
本题的解法，在于对更高层次递归的理解与运用。

(END)