ACM入门之组合数

Posted 2022-03-14 辉小歌

组合数模板一

const int N=2010;
const int mod=1e9+7;
int C[N][N],t,a,b;//C[i][j]  从i里面选j个
void init()

    for(int i=0;i<N;i++)
    
        for(int j=0;j<=i;j++)
        
            if(j==0) C[i][j]=1;
            else C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
        
    

组合数模板二

typedef long long int LL;
const int N=1e6+10;
const int mod=1e9+7;
LL f[N],inf[N],n;
LL quick_mi(LL a,LL b,LL p)

    LL sum=1;
    while(b)
    
        if(b&1) sum=sum*a%p;
        b>>=1;
        a=a*a%p;
    
    return sum%p;

void init()

    f[0]=1,inf[0]=1;
    for(int i=1;i<N;i++)
    
        f[i]=f[i-1]*i%mod;
        inf[i]=inf[i-1]*quick_mi(i,mod-2,mod)%mod;
    

LL query(LL a,LL b)//从a里面选b个

    return f[a]*inf[a-b]%mod*inf[b]%mod;

组合数模板三
0<=b<=a<=1e18

typedef long long int LL;
LL qmi(LL a,LL b, LL p)

	LL res=1;
	while(b)
	
		if(b&1) res=res*a%p;
		a=a*a%p;
		b=b>>1;
	
	return res;

LL C(LL a, LL b, LL p)

    if(b > a) return 0;
    if(b > a - b) b = a - b;
    LL x = 1, y = 1;
    for(int i = 0; i < b; i++)
    
        x = x * (a - i) % p;
        y = y * (i + 1) % p;
    
    return x * qmi(y, p - 2, p) % p;

LL lucas(LL a,LL b,LL p)

	if(a<p&&b<p) return C(a,b,p);
	return C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
 

组合数模板四
高精度

#include<bits/stdc++.h>
using namespace std;
const int N=5010;
int sum[N],prime[N],a,b,cnt;
bool st[N];
void init(int n)//打印质数表

    for(int i=2;i<=n;i++)
    
        if(!st[i]) prime[cnt++]=i;
        for(int j=0;prime[j]<=n/i;j++)
        
            st[prime[j]*i]=true;
            if(i%prime[j]==0) break;
        
    

int get(int n,int p)//求每个质数出现的次数

    int res=0;
    while(n) res+=n/p,n=n/p;
    return res;

vector<int> mul(vector<int> A,int b)

    vector<int> C;
    int t=0;
    for(int i=0;i<A.size()||t;i++)
    
        if(i<A.size()) t+=A[i]*b;
        C.push_back(t%10);
        t/=10;
    
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;

vector<int> ans;
int main(void)

    cin>>a>>b;
    init(a);
    ans.push_back(1);
    for(int i=0;i<cnt;i++) sum[i]=get(a,prime[i])-get(a-b,prime[i])-get(b,prime[i]);
    for(int i=0;i<cnt;i++) 
    
        for(int j=0;j<sum[i];j++) ans=mul(ans,prime[i]);
    
    for(int i=ans.size()-1;i>=0;i--) cout<<ans[i];
    return 0;

卡特兰数

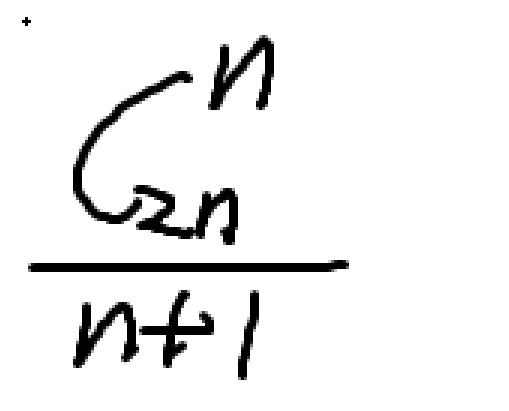
typedef long long int LL;
LL f[25],n;
LL get(int n)

    f[0]=1;
    for(int i=1; i<=n;i++) f[i]=f[i-1]*(4*i-2)/(i+1);
    return f[n];

885. 求组合数 I
886. 求组合数 II
887. 求组合数 III
888. 求组合数 IV