LeetCode 553 最优除法 HERODING的LeetCode之路[数学] HERODING的LeetCode之路

Posted 2022-03-01 HERODING23

解题思路：
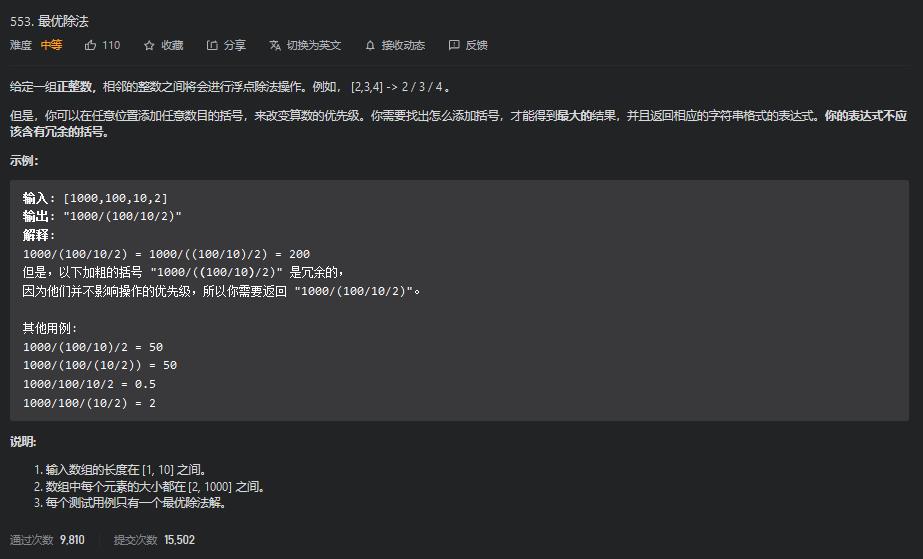
这道题本质是一个脑筋急转弯题目，仔细观察可以发现，分子是不变的，就是nums[0]，那么只要分母最小即可，什么时候分母最小呢，既然是一直除，那么分母也一直除就会越来越小，这样答案就明晰了，只要在第二个和末尾套括号即可，代码如下：

class Solution 
public:
    string optimalDivision(vector<int>& nums) 
        int n = nums.size();
        if(n == 1) 
            return to_string(nums[0]);
        
        if(n == 2) 
            return to_string(nums[0]) + '/' + to_string(nums[1]);
        
        string s = to_string(nums[0]) + "/(" + to_string(nums[1]);
        for(int i = 2; i < n; i ++) 
            s += '/' + to_string(nums[i]);
        
        s += ')';
        return s;
    
;