朝题夕解——DP之印章

Posted 2022-03-01 杨枝

🔔试题 算法训练 印章

• • 💒题目描述
  • 🌟解题报告
  • 🌻参考代码(C++版本)

💒题目描述

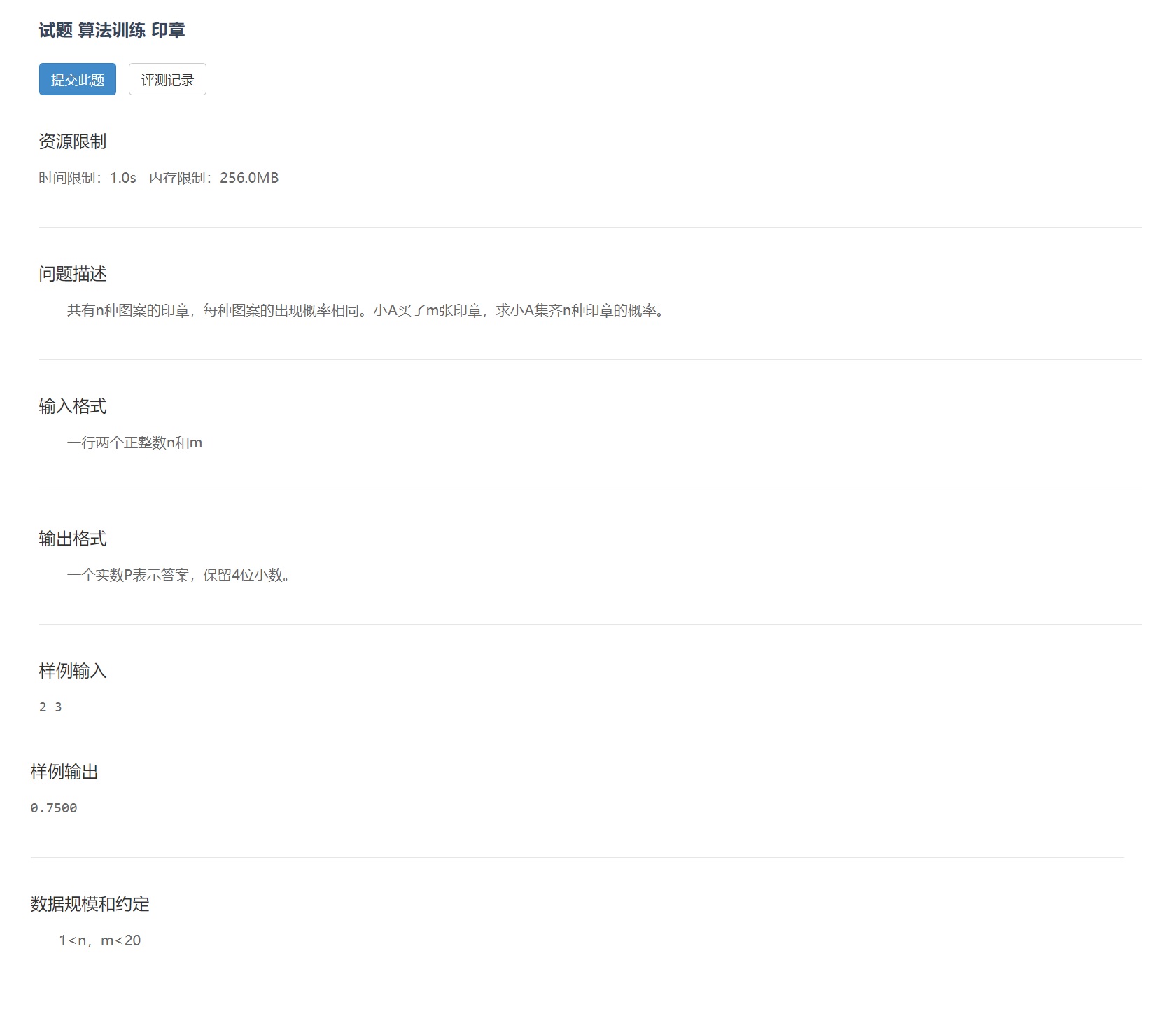
原题传送门
因为蓝桥的训练系统要登录，所以这个链接不一定跳转成功嗷~

🌟解题报告

一、锁定算法类型

问题描述是很简洁的，就洋洋洒洒的一句话，因为数据范围很小，再深思片刻，题目的意思应该是让我门找一个最优解，那么可以大致估计出来是一个DP问题。

二、状态表示

因为DP问题是自底向上的求解问题，那么我们就需要确定一个数组来记录其中状态，用于递推求解的过程。大多数的确定方式就是，题目问什么，就定一个数组表示这个问题。

我一般使用的是从集合的角度来分析DP问题。也就是大家耳熟能详的这是摘自某位小伙伴的总结——闫式DP分析法。感谢总结🌹🌹🌹

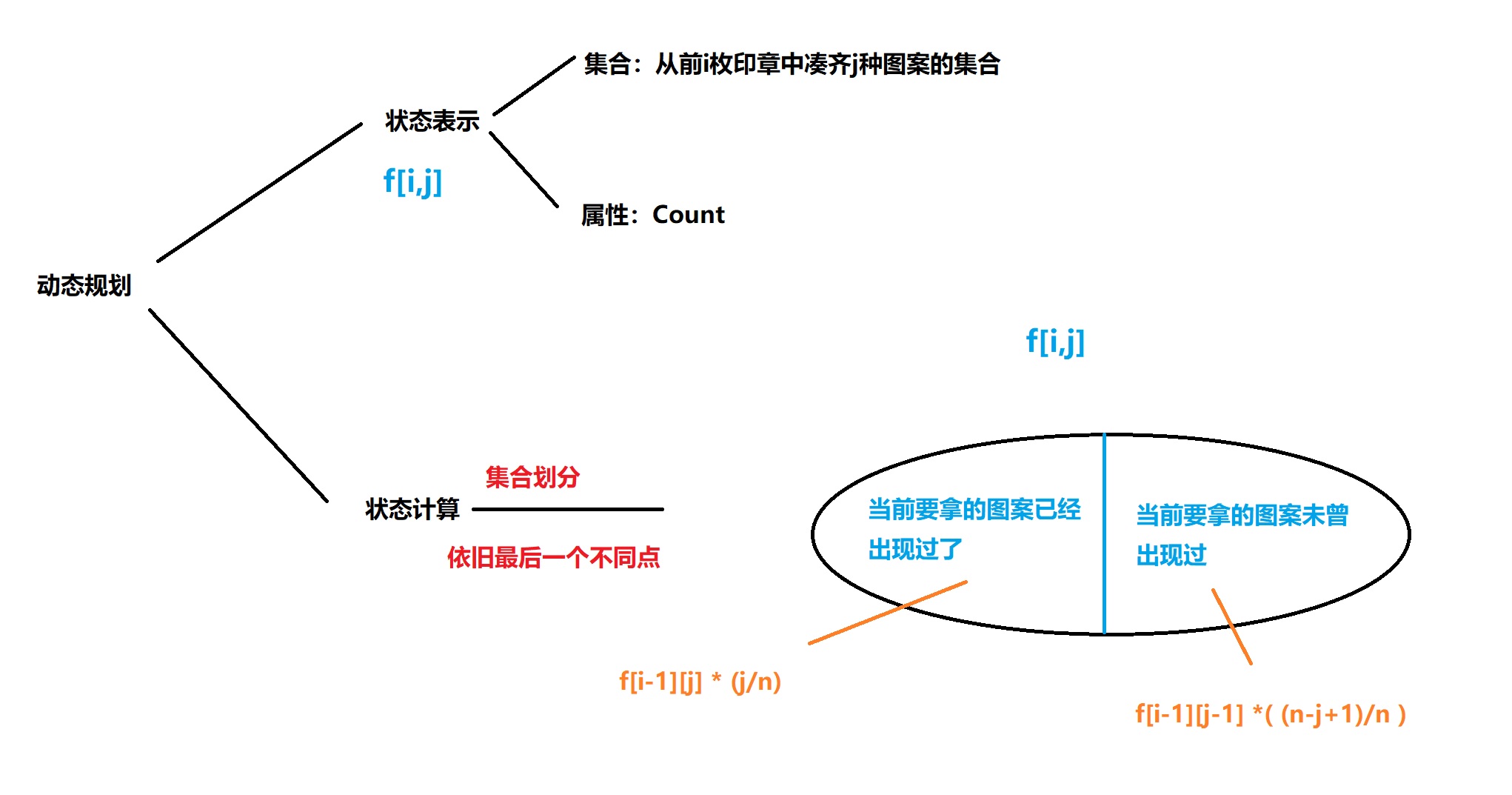
对于本题：
$f[i][j]$就表示从前$i$张印章凑齐$j$种图案的集合的概率。那么最后的答案也就是$f[m][n]$

三、状态计算

状态计算本质来说了，是对定义的这个集合进行划分的过程。划分的依据是最后一个不同点。


对于本题而言，最后一个不同点是：我现在正准备拿的这个图案是否已经和前面的重复了。


如果有重复，说明j种图案的印章已经凑齐了；如果没有重复，那就是还没有凑齐。

---

对于有重复：表示拿的前$i-1$枚印章中就已经凑出了$j$种图案，正要拿的这个第$i$枚印章，它上面的图案与之前拿的是有重复的了。所以获得图案的概率依旧是$j/n$
那么，状态转移方程为：f[i][j] = f[i-1][j]*(j/n)

---

对于无重复的：表示拿的前$i-1$枚印章中只是出现了$j-1$种图案，正要拿的这个第$i$枚印章应该是要凑齐的最后一种图案。因为前面已经出现了$j-1$种图案，剩下没有出现的就是总共有的$n$个图案减去已经出现的，即：$n-(j-1)$。这个时候，获得这枚图案的概率是：$(n-j+1)/n$
那么，状态转移方程为：f[i-1][j-1]*( (n-j+1)/n) )

---

觉得抽象的小伙伴可以重新想想这句话，动态规划是自底向上的递推。

我结合着无重复的情况进行带入演示。我现在总共要拿8种图案，我现在已经拿了2种图案，现在要递推到拿3种图案的情况。
那么我获得的这第3枚应该是在（8-2）= 6种进行选择嘛。我可能拿小脑虎，可能拿小花花，也可能是拿小太阳图案。总之，我获得它的概率是$6/8$

总结以上步骤，就可以得到如下这张图：

四、初始化
1、 $i<j$，就说明我们不可能凑齐，这个时候概率$fi][j]$=0

---

2、 $j=1$，就说明我们拿的$i$张印章里面，只要凑齐1种就行（ 是随便1种就可以了，就比如说 房子💒、星星🌟、花花🌻这三种，我拿房子图案出现1种概率，拿星星图案出现1种概率，拿花花图案也会出现1种，概率计算的时候就算的是这三种概率的和。）

其中$j=1$的时候我们也可以分两种情况：
①一种就是 $i=1$，这个时候就相当于我们的概率$f[i][j]=1$；

②另一种是 $i>1$，我有$i$种选择，每种选择会出现的概率是$1/n$，那么我们每个图案的概率都是$f[i][1]=(1/n{)}^i$；因为我们的图案不指定哪一种，所以我们的$f[i][j]$是$n$种图案的概率之和，倘若将$1/n$设定为$p$。那么概率就是$p^i\ast n$，化简之后就是$p^{i-1}$

🌻参考代码(C++版本)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>

using namespace std;
const int N = 25;
double f[N][N];//i张印章凑齐j种图案的概率
double p;//概率
int n,m;

int main()

	cin >> n >> m;
	p = 1.0/n;
	memset(f,0,sizeof(f));
	
	//DP
	for(int i = 1; i <= m;i++)//i张印章
		for(int j =1; j <= n;j++)//j种图案
		
			//当i小于j的时候，肯定是凑不齐的
			if(i < j) f[i][j] = 0;
			
			//当只用凑齐一个印章时
			//j只要所有图案中的一种就可以了，所以我们(1/n)^i还要再乘n，就是p^i-1
			else if(j == 1) f[i][1] = pow(p,i-1);
			
			//考虑当前这个j是否已经凑齐
			else f[i][j] = (f[i-1][j])*(j*p) + (f[i-1][j-1])*((n-j+1)*p);
		
	//输出结: m个印章，凑出n个图案
	printf("%.4lf\\n",f[m][n]);
	return 0;

总的来说，可能因为我现在写的DP题太少了，阐述起来还是挺啰嗦的。

还在慢慢精进。充满power~