NLP点滴——文本相似度，计算文本间的距离
Posted huanghanqian
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了NLP点滴——文本相似度，计算文本间的距离相关的知识，希望对你有一定的参考价值。
前言
在自然语言处理过程中，经常会涉及到如何度量两个文本之间的相似性，我们都知道文本是一种高维的语义空间，如何对其进行抽象分解，从而能够站在数学角度去量化其相似性。而有了文本之间相似性的度量方式，我们便可以利用划分法的K-means、基于密度的DBSCAN或者是基于模型的概率方法进行文本之间的聚类分析；另一方面，我们也可以利用文本之间的相似性对大规模语料进行去重预处理，或者找寻某一实体名称的相关名称（模糊匹配）。而衡量两个字符串的相似性有很多种方法，如最直接的利用hashcode，以及经典的主题模型或者利用词向量将文本抽象为向量表示，再通过特征向量之间的欧式距离或者皮尔森距离进行度量。本文围绕文本相似性度量的主题，从最直接的字面距离的度量到语义主题层面的度量进行整理总结，并将平时项目中用到的文本相似性代码进行了整理，如有任何纰漏还请指出，我会第一时间改正^v^。（ps.平时用的Java和scala较多，本文主要以Java为例。）
字面距离
提到如何比较两个字符串，我们从最初编程开始就知道：字符串有字符构成，只要比较比较两个字符串中每一个字符是否相等便知道两个字符串是否相等，或者更简单一点将每一个字符串通过哈希函数映射为一个哈希值，然后进行比较。但是这种方法有一个很明显的缺点，就是过于“硬”，对于相似性的度量其只有两种，0不相似，1相似，哪怕两个字符串只有一个字符不相等也是不相似，这在NLP的很多情况是无法使用的，所以下文我们就“软”的相似性的度量进行整理，而这些方法仅仅考虑了两个文本的字面距离，无法考虑到文本内在的语义内容。
common lang库
文中在部分代码应用中使用了Apache提供的common lang库，该库包含很多Java标准库中没有的但却很实用的函数。其maven引用如下：
<dependency>
<groupId>org.apache.commons</groupId> <artifactId>commons-lang3</artifactId> <version>3.4</version> </dependency>相同字符数
在传统的字符串比较过程中，我们考虑字符串中每个字符是否相等，并且考虑了字符出现的顺序，如果不考虑字符出现的顺序，我们可以利用两个文本之间相同的字符数量，很简单不再赘述，可以利用common lang中的getFuzzyDistance：
int dis = StringUtils.getFuzzyDistance(term, query, Locale.CHINA);莱文斯坦距离(编辑距离)
定义
我们在学习动态规划的时候，一个很经典的算法便是计算两个字符串的编辑距离，即：
莱文斯坦距离，又称Levenshtein距离，是编辑距离（edit distance）的一种。指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。
例如将kitten一字转成sitting：
- sitten （k→s）
- sittin （e→i）
- sitting （→g）
那么二者的编辑距离为3。
俄罗斯科学家弗拉基米尔·莱文斯坦在1965年提出这个概念。
实现方式
我们可以利用common lang中StringUtils的函数来计算：
int dis = StringUtils.getLevenshteinDistance(s1, s2);
//实现
public static int getLevenshteinDistance(CharSequence s, CharSequence t)
if (s == null || t == null)
throw new IllegalArgumentException("Strings must not be null");
int n = s.length(); // length of s
int m = t.length(); // length of t
if (n == 0)
return m;
else if (m == 0)
return n;
if (n > m)
// swap the input strings to consume less memory
final CharSequence tmp = s;
s = t;
t = tmp;
n = m;
m = t.length();
int p[] = new int[n + 1]; //'previous' cost array, horizontally
int d[] = new int[n + 1]; // cost array, horizontally
int _d[]; //placeholder to assist in swapping p and d
// indexes into strings s and t
int i; // iterates through s
int j; // iterates through t
char t_j; // jth character of t
int cost; // cost
for (i = 0; i <= n; i++)
p[i] = i;
for (j = 1; j <= m; j++)
t_j = t.charAt(j - 1);
d[0] = j;
for (i = 1; i <= n; i++)
cost = s.charAt(i - 1) == t_j ? 0 : 1;
// minimum of cell to the left+1, to the top+1, diagonally left and up +cost
d[i] = Math.min(Math.min(d[i - 1] + 1, p[i] + 1), p[i - 1] + cost);
// copy current distance counts to 'previous row' distance counts
_d = p;
p = d;
d = _d;
// our last action in the above loop was to switch d and p, so p now
// actually has the most recent cost counts
return p[n];
Jaro距离
定义
Jaro Distance也是字符串相似性的一种度量方式，也是一种编辑距离，Jaro 距离越高本文相似性越高;而Jaro–Winkler distance是Jaro Distance的一个变种。据说是用来判定健康记录上两个名字是否相同，也有说是是用于人口普查。从最初其应用我们便可看出其用法和用途，其定义如下：
其中
是匹配数目（保证顺序相同）
字符串长度
是换位数目
其中t换位数目表示：两个分别来自S1和S2的字符如果相距不超过
我们就认为这两个字符串是匹配的；而这些相互匹配的字符则决定了换位的数目t，简单来说就是不同顺序的匹配字符的数目的一半即为换位的数目t，举例来说，MARTHA与MARHTA的字符都是匹配的，但是这些匹配的字符中，T和H要换位才能把MARTHA变为MARHTA,那么T和H就是不同的顺序的匹配字符，t=2/2=1。
而Jaro-Winkler则给予了起始部分就相同的字符串更高的分数，他定义了一个前缀p，给予两个字符串，如果前缀部分有长度为 的部分相同，则Jaro-Winkler Distance为：
是两个字符串的Jaro Distance
是前缀的相同的长度，但是规定最大为4
则是调整分数的常数，规定不能超过0.25，不然可能出现dw大于1的情况，Winkler将这个常数定义为0.1
举个简单的例子：
计算
的距离
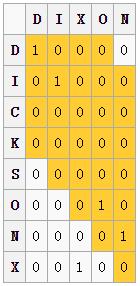
我们利用
可以得到一个匹配窗口距离为3，图中黄色部分便是匹配窗口，其中1表示一个匹配，我们发现两个X并没有匹配，因为其超出了匹配窗口的距离3。我们可以得到：
其Jaro score为：
而计算Jaro–Winkler score，我们使用标准权重
，其结果如下：
实现方式
同样我们可以利用common lang中的getJaroWinklerDistance函数来实现，注意这里实现的是Jaro–Winkler distance
double dis = StringUtils.getJaroWinklerDistance(reviewName.toLowerCase(), newsName.toLowerCase());
//实现
public static double getJaroWinklerDistance(final CharSequence first, final CharSequence second)
final double DEFAULT_SCALING_FACTOR = 0.1; //标准权重
if (first == null || second == null)
throw new IllegalArgumentException("Strings must not be null");
final double jaro = score(first,second); // 计算Jaro score
final int cl = commonPrefixLength(first, second); // 计算公共前缀长度
final double matchScore = Math.round((jaro + (DEFAULT_SCALING_FACTOR * cl * (1.0 - jaro))) *100.0)/100.0; // 计算 Jaro-Winkler score
return matchScore;
应用
在Wetest舆情监控中，我们在找寻游戏名简称和全称的对应关系时便使用到了Jaro-Winkler score进行衡量，其中我们将Jaro分数大于0.6的认为是相似文本，之后在总的相似文本中提取最相似的作为匹配项，实现效果还不错：
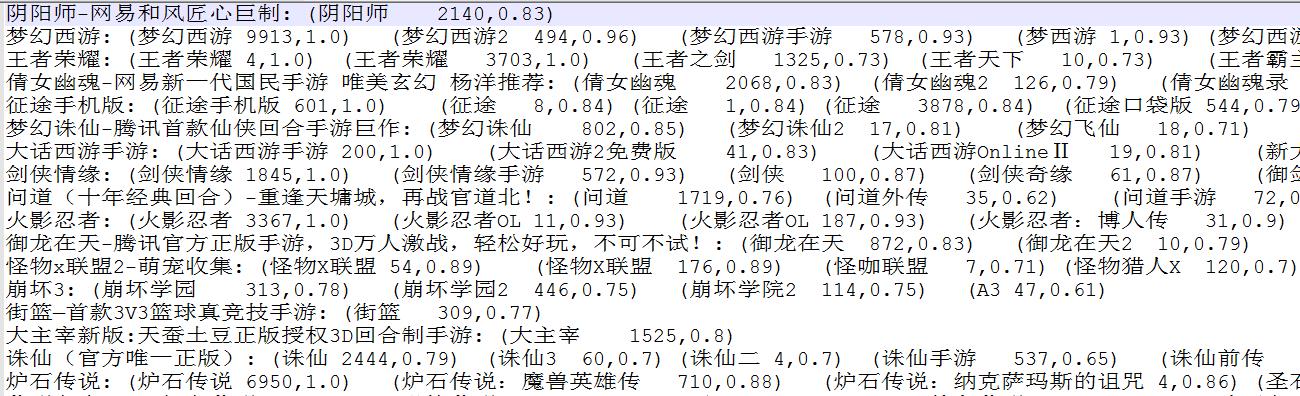
其中冒号左边是待匹配项，右边是匹配项<游戏名 词频，Jaro-Winkler score>，Jaro-Winkler score较高的一般都是正确的匹配项。
SimHash
定义
SimHash是一种局部敏感hash，它也是Google公司进行海量网页去重使用的主要算法。
传统的Hash算法只负责将原始内容尽量均匀随机地映射为一个签名值，原理上仅相当于伪随机数产生算法。传统的hash算法产生的两个签名，如果原始内容在一定概率下是相等的；如果不相等，除了说明原始内容不相等外，不再提供任何信息，因为即使原始内容只相差一个字节，所产生的签名也很可能差别很大。所以传统的Hash是无法在签名的维度上来衡量原内容的相似度，而SimHash本身属于一种局部敏感哈希算法，它产生的hash签名在一定程度上可以表征原内容的相似度。
我们主要解决的是文本相似度计算，要比较的是两个文章是否相似，当然我们降维生成了hash签名也是用于这个目的。看到这里估计大家就明白了，我们使用的simhash就算把文章中的字符串变成 01 串也还是可以用于计算相似度的，而传统的hash却不行。
我们可以来做个测试，两个相差只有一个字符的文本串，“你妈妈喊你回家吃饭哦，回家罗回家罗” 和 “你妈妈叫你回家吃饭啦，回家罗回家罗”。
通过simhash计算结果为：
1000010010101101111111100000101011010001001111100001001011001011
1000010010101101011111100000101011010001001111100001101010001011
通过传统hash计算为：
0001000001100110100111011011110
1010010001111111110010110011101
通过上面的例子我们可以很清晰的发现simhash的局部敏感性，相似文本只有部分01变化，而hash值很明显，即使变化很小一部分，也会相差很大。
基本流程
注：具体的事例摘自Lanceyan[10]的博客《海量数据相似度计算之simhash和海明距离》
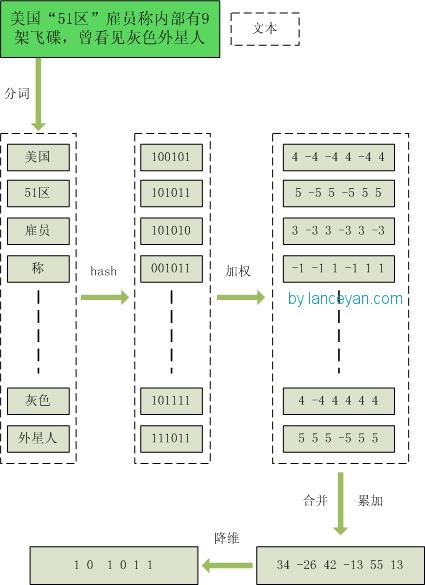
- 分词，把需要判断文本分词形成这个文章的特征单词。最后形成去掉噪音词的单词序列并为每个词加上权重，我们假设权重分为5个级别（1~5）。比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”，括号里是代表单词在整个句子里重要程度，数字越大越重要。
- hash，通过hash算法把每个词变成hash值，比如“美国”通过hash算法计算为 100101,“51区”通过hash算法计算为 101011。这样我们的字符串就变成了一串串数字，还记得文章开头说过的吗，要把文章变为数字计算才能提高相似度计算性能，现在是降维过程进行时。
- 加权，通过 2步骤的hash生成结果，需要按照单词的权重形成加权数字串，比如“美国”的hash值为“100101”，通过加权计算为“4 -4 -4 4 -4 4”；“51区”的hash值为“101011”，通过加权计算为 “ 5 -5 5 -5 5 5”。
- 合并，把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。这里作为示例只算了两个单词的，真实计算需要把所有单词的序列串累加。
- 降维，把4步算出来的 “9 -9 1 -1 1 9” 变成 0 1 串，形成我们最终的simhash签名。 如果每一位大于0 记为 1，小于0 记为 0。最后算出结果为：“1 0 1 0 1 1”。
整个过程的流程图为：
相似性度量
有了simhash值，我们需要来度量两个文本间的相似性，就像上面的例子一样，我们可以比较两个simhash间0和1不同的数量。这便是汉明距离（Hamming distance）
在信息论中，两个等长字符串之间的汉明距离（英语：Hamming distance）是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
汉明重量是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是1的个数，所以11101的汉明重量是4。
例如：
1011101与1001001之间的汉明距离是2
一般在利用simhash进行文本相似度比较时，我们认为汉明距离小于3的文本是相似的。
存储索引
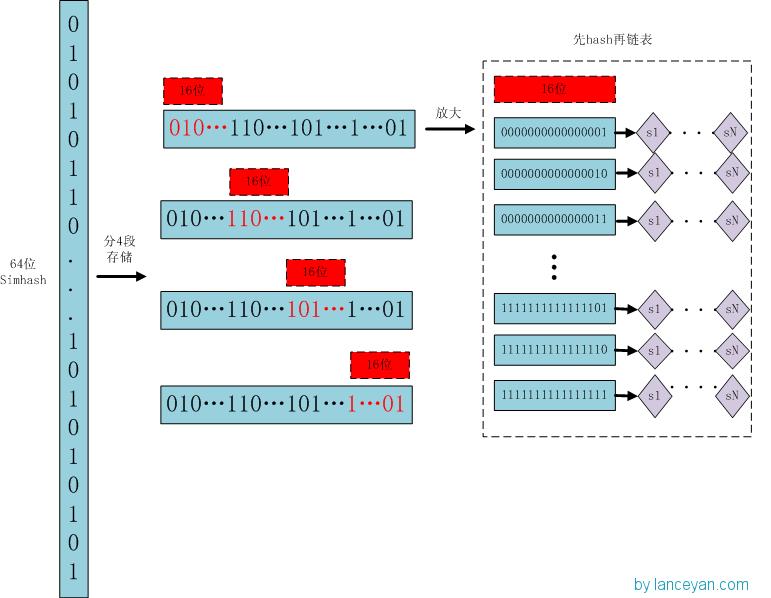
存储：
- 将一个64位的simhash签名拆分成4个16位的二进制码。（图上红色的16位）
- 分别拿着4个16位二进制码查找当前对应位置上是否有元素。（放大后的16位）
- 对应位置没有元素，直接追加到链表上；对应位置有则直接追加到链表尾端。（图上的 S1 — SN）
查找：
- 将需要比较的simhash签名拆分成4个16位的二进制码。
- 分别拿着4个16位二进制码每一个去查找simhash集合对应位置上是否有元素。
- 如果有元素，则把链表拿出来顺序查找比较，直到simhash小于一定大小的值，整个过程完成。
- 在去重时，因为汉明距离小于3则为重复文本，那么如果存在simhash相似的文本，对于四段simhash则至少有一段simhash是相同的，所以在去重时对于待判断文本D，如果D中每一段的simhash都没有相同的，那么D为无重复文本。
原理：
借鉴hashmap算法找出可以hash的key值，因为我们使用的simhash是局部敏感哈希，这个算法的特点是只要相似的字符串只有个别的位数是有差别变化。那这样我们可以推断两个相似的文本，至少有16位的simhash是一样的。具体选择16位、8位、4位，大家根据自己的数据测试选择，虽然比较的位数越小越精准，但是空间会变大。分为4个16位段的存储空间是单独simhash存储空间的4倍。
实现
在实际NLP的使用中，我利用Murmur3作为字符串的64位哈希值，用Java和spark分别实现了一个simhash的版本
我将源码放在了github上，如下链接：
github: xlturing/simhashJava
其中利用了结巴作为文本的分词工具，Murmur3用来产生64位的hashcode。另外根据上述存储方式，进行了simhash分段存储，提高搜索速度，从而进行高效查重。
应用
simhash从最一开始用的最多的场景便是大规模文本的去重，对于爬虫从网上爬取的大规模语料数据，我们需要进行预处理，删除重复的文档才能进行后续的文本处理和挖掘，那么利用simhash是一种不错的选择，其计算复杂度和效果都有一个很好的折中。
但是在实际应用过程中，也发现一些badcase，完全无关的文本正好对应成了相同的simhash，精确度并不是很高，而且simhash更适用于较长的文本，但是在大规模语料进行去重时，simhash的计算速度优势还是很不错的。
语义相似性
在NLP中有时候我们度量两个短文本或者说更直接的两个词语的相似性时，直接通过字面距离是无法实现的，如：中国-北京，意大利-罗马，这两个短语之间的相似距离应该是类似的，因为都是首都与国家的关系；再比如（男人、男孩），（女人、女孩）应该是相同的关系，但是我们看其字面距离都是0。
想要做到语义层面的度量，我们需要用到机器学习建模，而自然语言的问题转化为机器学习的首要问题便是找到一种方法把自然语言的符号数学化。
背景知识
在自然语言处理领域中，有两大理论方向，一种是基于统计的经验主义方法，另一种是基于规则的理性主义方法[15]。而随着计算机性能的提升，以及互联网发展而得到的海量语料库，目前NLP的研究更多是基于统计的经验主义方法。所以在本文讨论的语义相似性中，也是从统计学的角度出发进行总结。
统计语言模型
对于统计语言模型而言，最基础的理论便是贝叶斯理论（Bayes' theorem PS.关于贝叶斯理论强烈推荐：数学之美番外篇：平凡而又神奇的贝叶斯方法，一篇深入浅出的好文。另外推荐下自己师兄参与翻译的作品《贝叶斯方法——概率编程与贝叶斯推断》很全面的贝叶斯理论+实践书籍）。对于大规模语料库，我们可以通过词频的方式来获取概率，例如100个句子中，出现了1次"Okay"，那么
而同样的对于句子"An apple ate the chicken"我们可以认为其概率为0，因为这不符合我们说话的逻辑。
统计语言模型是用来计算一个句子的概率，其通常基于一个语料库D来构建。如何表示一个句子的概率呢？我们用
来表示一个基元（通常就是指词语，也可以是字或短语），那么对于一个由N个词组成的句子W可以表示为
那么其联合概率
就可以认为是该句子的概率，根据贝叶斯公式的链式法则可以得到：
其中条件概率
便是语言模型的参数，如果我们把这些全部算出来，那么一个句子的概率我们就能很轻易的得出。但是很明显，这个参数的量是巨大的是无法计算的。这时我们可以将
映射到某个等价类
，从而降低参数数目。
ps.语料库我们用C表示，而词典D一般为语料中出现的所有不重复词
n-gram模型
既然每个单词依赖的单词过多，从而造成了参数过多的问题，那么我们就简单点，假设每个单词只与其前n-1个单词有关，这便是n-1阶Markov假设，也就是n-gram模型的基本思想。
那么对于句子W的概率我们可以简化如下：
那么对于最简单的一阶情况也称unigram或uni-gram或monogram（二阶bigram 三阶trigram）就简单表示为
为了在句首和句尾能够统一，我们一般会在句首加一个BOS标记，句尾加一个EOS标记，那么对于句子"Mark wrote a book"，其概率可以表示如下：
为了预估
条件概率，根据大数定理，简单统计语料库中
出现的频率，并进行归一化。我们用c来表示频率，那么可表示如下：
其中分母在unigram中就可以简单认为是词语
出现的次数。
在n-gram模型中还有一个很重要的问题就是平滑化，因为再大的语料库都不可能涵盖所有情况，考虑两个问题：
那么
就是0吗？
那么就是1吗？
这显然是不合理的，这就需要进行平滑，这里不展开讨论。
根据最大似然，我们可以得到：
其中C表示语料库，
表示词语的上下文，而这里对于n-gram模型
，取对数后的对数似然函数为：
从上式我们可以看出
可以看做是
关于的函数，即：
其中
为待定参数集，通过语料库训练得到参数集后，F便确定了，我们不需要再存储概率，可以直接计算得到，而语言模型中很关键的就在于F的构造
词向量
为了从使得计算机从语义层面理解人类语言，首先要做的就是将语言数学化，如何进行表示呢？人们便提出了词向量的概念，即用一个向量来表示一个词。
One-hot Representation
一种最简单词向量就是利用词频向量将高维的语义空间抽象成数学符号表示，向量长度为词典
的大小
，这种表示方式非常直观，但是容易造成维度灾难，并且还是不能刻画语义的信息。
词语表示
对于词语而言，用一个向量来表示一个词，最直观简单的方式就是将每个词变为一个很长的向量，向量长度便是词典的长度，其中绝大部分为0，只有一个维度为1代表了当前词。
假设语料库：“冲突容易引发战争”，那么词典为
- D=[冲突,容易,引发,战争]
- 冲突=[1,0,0,0]
- 战争=[0,0,0,1]
每个词都是含有一个1的n维向量（
），这种方式我们压缩存储下，就是给每个词语分配一个ID，通常实际变成我们最简单的就是用hash值表示一个词语。这种方式可以用在SVM、最大熵和CRF等等算法中，完成NLP的大多数场景。例如，我们可以直接将
但是缺点很明显，就是我们用这种方式依旧无法度量两个词的语义相似性，任意两个词之间都是孤立的，比如上面的冲突和战争是近义词，但是却没有任何关联性。
文档表示
同样文档也可以用词频向量的形式来表示，一般我们会利用tf-idf作为每一个词的特征值，之后会挑选每篇文档比较重要的部分词来表示一篇文档，拿游戏来说，如下：
[王者荣耀, 阴阳师, 梦幻西游]
- doc1:[tf-idf(王者荣耀), tf-idf(阴阳师), tf-idf(梦幻西游)]
- doc2:[tf-idf(王者荣耀), tf-idf(阴阳师), tf-idf(梦幻西游)]
然后我们就可以利用K-means等聚类算法进行聚类分析，当然对于每篇文档，一般我们只会选取部分词汇，因为如果词汇过多可能造成NLP中常见的维度“灾难”。这种方式在大多数NLP场景中都是适用的，但是由于这种表示往往是建立在高维空间，为了避免维度灾难就要损失一定的语义信息，这也是这种方法的弊端。
Distributed representation
另外一种词向量的表示Distributed representation最早由 Hinton在 1986年提出。它是一种低维实数向量，这种向量一般长成这个样子：
[0.792, −0.177, −0.107, 0.109, −0.542, …]
维度以 50 维和 100 维比较常见，当然了，这种向量的表示不是唯一的。
Distributed representation的关键点在于，将高维空间中的词汇映射到一个低维的向量空间中，并且让相关或者相似的词，在距离上更接近（看到这里大家有没有想到普通hash以及simhash的区别呢？），这里引用一张图片（来自[13]）：
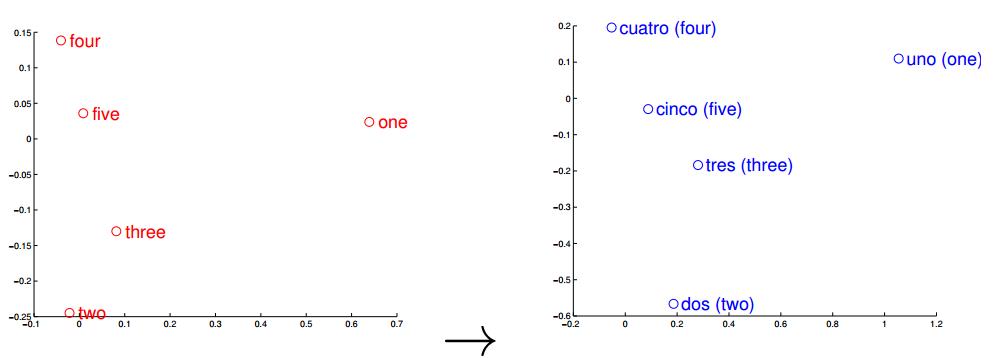
图中是英语和西班牙语通过训练分别得到他们的词向量空间，之后利用PCA主成分分析进行降维表示在二维坐标图中的。我们可以清晰的看出，对于两种语系的一二三四五，在空间距离上竟是如此的相似，这就是Distributed representation词向量表示的意义所在。
这种采用低维空间表示法，不但解决了维数灾难问题，并且挖掘了word之间的关联属性，从而提高了向量语义上的准确度，下面我们讨论的语言模型都是基于这种词向量表示方式。
PS. 有时候也会出现Word Represention或 Word Embedding(所谓词嵌入)的说法。另外我们这里说的词向量是在词粒度进行分析，当然我们也可以在字粒度的字向量、句子粒度的句向量以及文档粒度的文档向量进行表示分析。
主题模型
在长文本的篇章处理中，主题模型是一种经典的模型，经常会用在自然语言处理、推荐算法等应用场景中。本节从LDA的演变过程对LDA进行阐述，然后就LDA在长文本相似性的判断聚类上做简要说明。
LSA
首先对于一篇文档Document，词语空间的一个词频向量
如下：
其中每个维度表示某一词语term在该文档中出现的次数，最终对于大量的训练样本，我们可以得到训练样本的矩阵X，如下图：
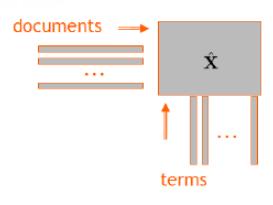
LSA的基本思想，便是利用最基本的SVD奇异值分解，将高维语义空间映射到低维空间，其流程如下：
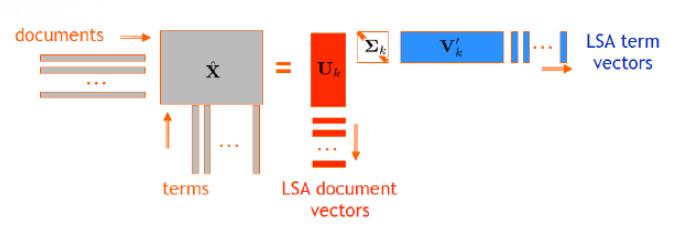
这样对于训练样本中词表的每一个term我们便得到了一个低维空间的向量表示。但LSA的显著问题便是值考虑词频，并不区分同一词语的不同含义
PLSA
LSA基于最基本的SVD分解，但缺乏严谨的数理统计逻辑，于是Hofmann提出了PLSA，其中P便是Probabilistic，其基本的假设是每个文档所表示的词频空间向量w服从多项式分布（Multinomial distribution）
简单扯两句多项式分布：
-
伯努利分布（Bernoulli distribution）我们从接触概率论开始便知道，即所谓的投硬币，其离散分布如下：
但是吊吊的数学家们总喜欢做一些优雅的让人看不懂的事情，所以也可以写作如下公式：
其中k为0或者1 -
二项分布（Binomial distribution）：
如果进行次投硬币实验，计算出现m次正面朝上的概率
伯努利分布是二项分布中n=1时的特殊情况 -
Categorical分布（Categorical distribution），如果我们将投硬币改成掷骰子，那么原来一维向量x就会变成一个六维向量，其中每一维度为1表示出现该面，0表示没出现，用数学表示即对于随机变量X有k中情况，其中第
种情况出现的概率为
：
那么我们可以得到其离散概率分布如下：
其中如果
那么
为1，否则为0 -
多项式分布（Multinomial distribution）：与二项分布类似，Categorical分布进行N次试验，便得到多项式分布：
同样我们可以写成吊吊的形式：
其中
为gamma函数：当n>0，则
（ps.该形式与狄利克雷分布（Dirichlet distribution）的形式非常相似，因为多项式分布是狄利克雷分布的共轭先验）
OK简单梳理了下过去的知识，PLSA假设每篇文档的词频向量服从Categorical分布，那么对于整个训练样本的词频矩阵W则服从多项式分布。PLSA利用了aspect model，引入了潜在变量z（即所谓主题），使其变成一个混合模型（mixture model）。其图模型如下：
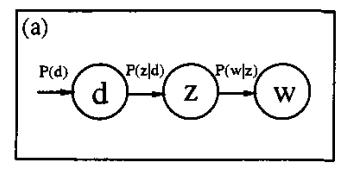
其中
表示文档集，Z便是PLSA中引入的隐含变量（主题/类别），
表示词表。
表示单词出现在文档
的概率，
表示文档
中出现主题
下的单词的概率，
给定主题
出现单词
的概率。其中每个主题在所有词项上服从Multinomial分布，每个文档在所有主题上服从Multinmial分布。按照生成模型，整个文档的生成过程如下：
(1)以的概率生成文档
(2)以的概率选中主题
(3)以的概率产生一个单词
那么对于单词出现在文档的联合概率分布，而是隐含变量。
自然语言处理（NLP）基于PaddleNLP的短文本相似度计算