数据机构与算法之深入解析“完美矩形”的求解思路与算法示例

Posted 2022-02-21 Serendipity·y

一、题目要求

• 给你一个数组 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形，这个矩形的左下顶点是 (xi, yi) ，右上顶点是 (ai, bi) 。
• 如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。
• 示例 1：

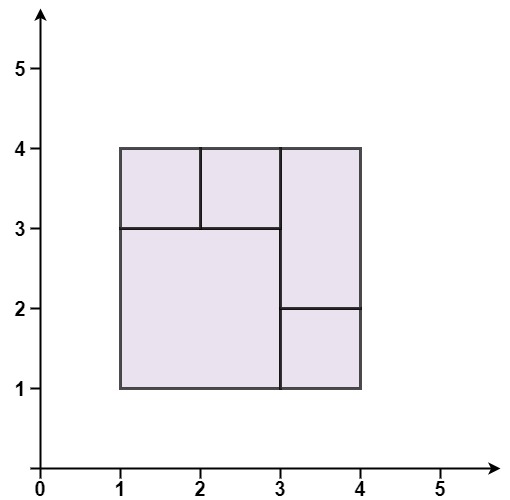
输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。 

• 示例 2：

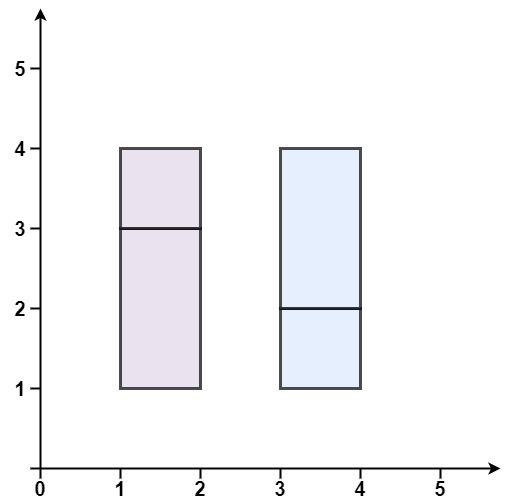
输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

• 示例 3：

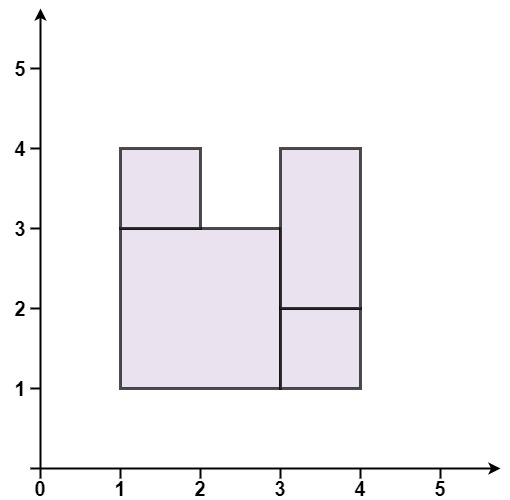
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
输出：false
解释：图形顶端留有空缺，无法覆盖成一个矩形。

• 提示：
• • 1 <= rectangles.length <= 2 * 10⁴；
• • rectangles[i].length == 4；
• • -10⁵ <= x_I, y_I, a_I, b_I <= 10⁵。

二、思路分析

• 如下所示，第 1 个例子是满足要求的，后面 2 个都不满足要求：

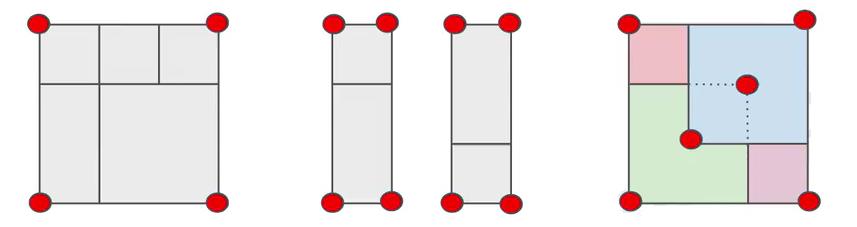
• 第 1 个例子有 4 个与其他顶点不重叠的外围顶点，第 2 个例子有 8 个这样的外围顶点，第 3 个例子有 6 个这样的外围顶点：

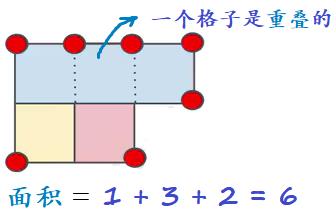
• 黄色 1 + 蓝色 3 + 红色(实际应该包含重叠的面积1) = 1+3+2=6，但末尾缺了一块，且出现了重叠，不是完美矩形。
• 如下图所示，就是完美矩形：

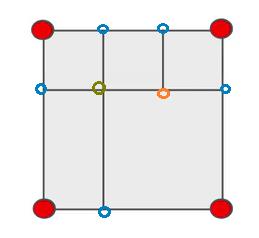
• 完美矩形的性质：
• • 只有最外围的 4 个顶点会出现 1 次；
• • 边缘上，5 个蓝色的点作为顶点被 2 个长方形共用，总共会出现 2 次；
• • 中间(inner case)的深黄色的点作为顶点被 4 个长方形共用，总共会出现 4 次；
• • 中间的橙色的点作为顶点被 2 个长方形共用，总共会出现 2 次。
• 分析可知，完美矩形应满足如下要求：
• • 正好 4 个外围顶点（不与其他任何顶点重叠或覆盖）；
• • ∑area_i = 4 个角落顶点形成的封闭区域的面积。

三、求解算法

① 哈希 set 实现

• 使用哈希 set 存储各个顶点出现的次数；
• 只出现 1 次的顶点的数量恰好是 4 个；
• 所有小的长方形的面积之和 = 最大长方形的面积；
• 这样就能确保形成完美的矩形。
• C++ 示例：

typedef long long LL;
class Solution 
public:
    bool isRectangleCover(vector<vector<int>>& rectangles) 
        set<pair<LL, LL>> corners;
        LL area = 0;
        for (const auto& rect : rectangles)
        
            pair<LL, LL> p1rect[0], rect[1]; /* 对每个矩形, 分别逆时针地取4个顶点p1, p2, p3, p4 */
            pair<LL, LL> p2rect[2], rect[1];
            pair<LL, LL> p3rect[2], rect[3];
            pair<LL, LL> p4rect[0], rect[3];
            for (const auto& p : p1, p2, p3, p4)
            
                const auto& op = corners.insert(p); /* 记录是否能成功插入到set中 */
                if (!op.second)
                    corners.erase(op.first); /* 能配成对(出现次数为2或4的)的, 将它们从set中删掉, 如果能形成完美矩形, 最后剩下的顶点个数必然为4 */
            
            area += (p3.first - p1.first) * (p3.second - p1.second);
        
        if (corners.size() != 4)
            return false;
        const auto& p1 = *(corners.begin()); /* set会自动从小到大排序, 于是set的第1个元素p1是左下角的点, p3是右上角的点 */
        const auto& p3 = *(corners.rbegin());
        return area == (p3.first - p1.first) * (p3.second - p1.second);
    
;

② 哈希表

• 精确覆盖意味着：
• • 矩形区域中不能有空缺，即矩形区域的面积等于所有矩形的面积之和；
• • 矩形区域中不能有相交区域。
• 需要一个统计量来判定是否存在相交区域，由于精确覆盖意味着矩形的边和顶点会重合在一起，不妨统计每个矩形顶点的出现次数。同一个位置至多只能存在四个顶点，在满足该条件的前提下，如果矩形区域中有相交区域，这要么导致矩形区域四角的顶点出现不止一次，要么导致非四角的顶点存在出现一次或三次的顶点；
• 因此要满足精确覆盖，除了要满足矩形区域的面积等于所有矩形的面积之和，还要满足矩形区域四角的顶点只能出现一次，且其余顶点的出现次数只能是两次或四次。
• 在代码实现时，我们可以遍历矩形数组，计算矩形区域四个顶点的位置，以及矩形面积之和，并用哈希表统计每个矩形的顶点的出现次数。遍历完成后，检查矩形区域的面积是否等于所有矩形的面积之和，以及每个顶点的出现次数是否满足上述要求。
• C++ 示例：

class Solution 
public:
    bool isRectangleCover(vector<vector<int>>& R) 
        map<pair<int, int>, int> dict; // 记录每个点出现的次数
        typedef long long LL;
        LL sum = 0; // 小矩形的面积和
        for (auto& x : R) // 左上角是(a, b)右下角是(c, d)
        
            LL a = x[0], b = x[1], c = x[2], d = x[3];
            ++dict[a, b], ++dict[a, d];
            ++dict[c, b], ++dict[c, d];
            sum += (c - a) * (d - b); // 计算总面积, 可能爆int所以用long long来存
        
        vector<vector<int>> res; // 计算一下每个点出现的次数，记录一下只出现一次的点
        for (auto& [x, y] : dict)
            if (y == 1)
                res.push_back(x.first, x.second);
            else if (y == 3) // 如果有点出现3次就不是
                return false;
            else if (y > 4)
                return false;
        if (res.size() != 4)  // 出现1次的点必须恰好是4个
            return false;
        return sum == (LL)(res[3][0] - res[0][0]) * (res[3][1] - res[0][1]);
    
;

③ 扫描线

• 将每个矩形 rectangles[i] 看做两条竖直方向的边，使用 (x,y1,y2) 的形式进行存储（其中 y1 代表该竖边的下端点，y2 代表竖边的上端点），同时为了区分是矩形的左边还是右边，再引入一个标识位，即以四元组 (x,y1,y2,flag) 的形式进行存储。
• 一个完美矩形的充要条件为：对于完美矩形的每一条非边缘的竖边，都「成对」出现（存在两条完全相同的左边和右边重叠在一起）；对于完美矩形的两条边缘竖边，均独立为一条连续的（不重叠）的竖边。
• 如图（红色框的为「完美矩形的边缘竖边」，绿框的为「完美矩形的非边缘竖边」）：

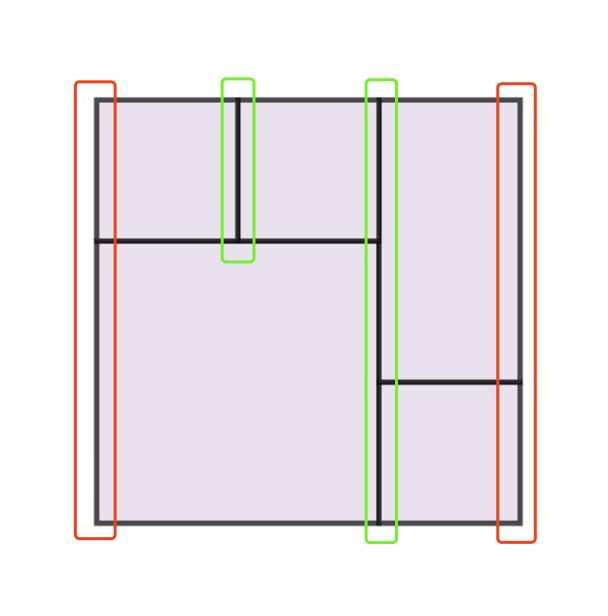
• 绿色：非边缘竖边必然有成对的左右两条完全相同的竖边重叠在一起；
• 红色：边缘竖边由于只有单边，必然不重叠，且连接成一条完成的竖边。
• Java 示例：

class Solution 
    public boolean isRectangleCover(int[][] rectangles) 
        int n = rectangles.length;
        int[][] rs = new int[n * 2][4];
        for (int i = 0, idx = 0; i < n; i++) 
            int[] re = rectangles[i];
            rs[idx++] = new int[]re[0], re[1], re[3], 1;
            rs[idx++] = new int[]re[2], re[1], re[3], -1;
        
        Arrays.sort(rs, (a,b)->
            if (a[0] != b[0]) return a[0] - b[0];
            return a[1] - b[1];
        );
        n *= 2;
        // 分别存储相同的横坐标下「左边的线段」和「右边的线段」 (y1, y2)
        List<int[]> l1 = new ArrayList<>(), l2 = new ArrayList<>(); 
        for (int l = 0; l < n; ) 
            int r = l;
            l1.clear(); l2.clear();
            // 找到横坐标相同部分
            while (r < n && rs[r][0] == rs[l][0]) r++;
            for (int i = l; i < r; i++) 
                int[] cur = new int[]rs[i][1], rs[i][2];
                List<int[]> list = rs[i][3] == 1 ? l1 : l2;
                if (list.isEmpty()) 
                    list.add(cur);
                 else 
                    int[] prev = list.get(list.size() - 1);
                    if (cur[0] < prev[1]) return false; // 存在重叠
                    else if (cur[0] == prev[1]) prev[1] = cur[1]; // 首尾相连
                    else list.add(cur); 
                
            
            if (l > 0 && r < n) 
                // 若不是完美矩形的边缘竖边，检查是否成对出现
                if (l1.size() != l2.size()) return false;
                for (int i = 0; i < l1.size(); i++) 
                    if (l1.get(i)[0] == l2.get(i)[0] && l1.get(i)[1] == l2.get(i)[1]) continue;
                    return false;
                
             else 
                // 若是完美矩形的边缘竖边，检查是否形成完整一段
                if (l1.size() + l2.size() != 1) return false;
            
            l = r;
        
        return true;
    

• Python 示例：

class Solution:
    def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
        if not rectangles:
            return False
        n = len(rectangles)
        # 解析数据，(x, y, a, b) -> (x, y, b, 1) ，(a, y, b, -1)
        # 最后一位表示是矩形的左边缘还是右边缘（即扫描线的“上升”和“下降”）
        rs = []
        for rec in rectangles:
            x, y, a, b = rec
            rs.append([x, y, b, 1])
            rs.append([a, y, b, -1])
        rs.sort()
        
        l = r = 0
        while r < len(rs):
            l1 = [] # 记录“上升”的线段
            l2 = [] # 记录“下降”的线段
            while r < len(rs) and rs[r][0] == rs[l][0]:
                r += 1
            for i in range(l, r): # 遍历横坐标相同的线段
                x, y1, y2, isUp = rs[i]
                curl = l1 if isUp == 1 else l2 
                if not curl:
                    curl.append([y1, y2])
                else:
                    if curl[-1][1] > y1: # 有重叠
                        return False 
                    elif curl[-1][1] == y1: # 能连接上，进行连接
                        curl[-1][1] = y2 
                    else: # 不能连接上，记录新的一段
                        curl.append([y1, y2])
            # 若处理的是最左边的边或最右边的边，此时应连成一个线段
            if l == 0 or r == len(rs): 
                if len(l1) + len(l2) != 1:
                    return False 
            else:
                # 若处理的是中间的扫描线，此时上升的线段和下降的线段应完全相同才能正好重叠
                if len(l1) != len(l2):
                    return False 
                for i in range(len(l1)):
                    if l1[i] != l2[i]:
                        return False 
            l = r # 进入下一个横坐标的扫描
        return True