数据结构与算法之深入解析“通配符匹配”的求解思路与算法示例

Posted 2022-02-16 Serendipity·y

一、题目要求

• 给定一个字符串 (s) 和一个字符模式 § ，实现一个支持 ‘?’ 和 ‘*’ 的通配符匹配。
• • ‘?’ 可以匹配任何单个字符。
• • ‘*’ 可以匹配任意字符串（包括空字符串）。
• 两个字符串完全匹配才算匹配成功。
• 说明：
• • s 可能为空，且只包含从 a-z 的小写字母；
• • p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。
• 示例 1：

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

• 示例 2：

输入:
s = "aa"
p = "*"
输出: true
解释: '*' 可以匹配任意字符串。

• 示例 3：

输入:
s = "cb"
p = "?a"
输出: false
解释: '?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

• 示例 4：

输入:
s = "adceb"
p = "*a*b"
输出: true
解释: 第一个 '*' 可以匹配空字符串, 第二个 '*' 可以匹配字符串 "dce"

• 示例 5：

输入:
s = "acdcb"
p = "a*c?b"
输出: false

二、求解算法

① 动态规划

• 在给定的模式 p 中，只会有三种类型的字符出现：
• • 小写字母 a−z，可以匹配对应的一个小写字母；
• • 问号 ?，可以匹配任意一个小写字母；
• • 星号 ∗，可以匹配任意字符串，可以为空，也就是匹配零或任意多个小写字母。
• 其中「小写字母」和「问号」的匹配是确定的，而「星号」的匹配是不确定的，因此需要枚举所有的匹配情况。为了减少重复枚举，可以使用动态规划来解决本题。
• 用 dp[i][j] 表示字符串 s 的前 i 个字符和模式 p 的前 j 个字符是否能匹配。在进行状态转移时，我们可以考虑模式 p 的第 j 个字符 p_j，与之对应的是字符串 s 中的第 i 个字符 s_i：
• • 如果 p_j 是小写字母，那么 s_i 必须也为相同的小写字母，状态转移方程为：

• • 其中 ∧ 表示逻辑与运算，也就是说，dp[i][j] 为真，当且仅当 dp[i−1][j−1] 为真，并且 s_i 与 p_j 相同。
• • 如果 p_j 是问号，那么对 s_i 没有任何要求，状态转移方程为：

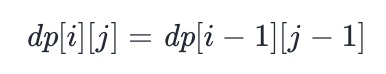
• • 如果 p_j 是星号，那么同样对 s_i 没有任何要求，但是星号可以匹配零或任意多个小写字母，因此状态转移方程分为两种情况，即使用或不使用这个星号：

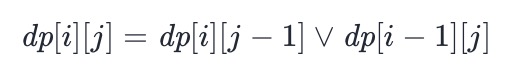
• • 其中 ∨ 表示逻辑或运算，如果不使用这个星号，那么就会从 dp[i][j−1] 转移而来；如果使用这个星号，那么就会从 dp[i−1][j] 转移而来。
• 最终的状态转移方程如下：

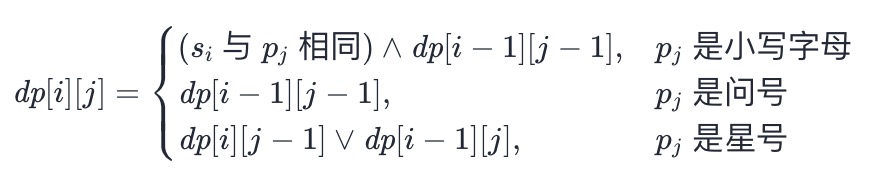
• 也可以将前两种转移进行归纳：

• C++ 示例：

class Solution 
public:
    bool isMatch(string s, string p) 
        int m = s.size();
        int n = p.size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        dp[0][0] = true;
        for (int i = 1; i <= n; ++i) 
            if (p[i - 1] == '*') 
                dp[0][i] = true;
            
            else 
                break;
            
        
        for (int i = 1; i <= m; ++i) 
            for (int j = 1; j <= n; ++j) 
                if (p[j - 1] == '*') 
                    dp[i][j] = dp[i][j - 1] | dp[i - 1][j];
                
                else if (p[j - 1] == '?' || s[i - 1] == p[j - 1]) 
                    dp[i][j] = dp[i - 1][j - 1];
                
            
        
        return dp[m][n];
    
;

• Java 示例：

class Solution 
    public boolean isMatch(String s, String p) 
        int m = s.length();
        int n = p.length();
        boolean[][] dp = new boolean[m + 1][n + 1];
        dp[0][0] = true;
        for (int i = 1; i <= n; ++i) 
            if (p.charAt(i - 1) == '*') 
                dp[0][i] = true;
             else 
                break;
            
        
        for (int i = 1; i <= m; ++i) 
            for (int j = 1; j <= n; ++j) 
                if (p.charAt(j - 1) == '*') 
                    dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
                 else if (p.charAt(j - 1) == '?' || s.charAt(i - 1) == p.charAt(j - 1)) 
                    dp[i][j] = dp[i - 1][j - 1];
                
            
        
        return dp[m][n];
    

② 贪心算法

• 方法①的瓶颈在于对星号 ∗ 的处理方式：使用动态规划枚举所有的情况。由于星号是「万能」的匹配字符，连续的多个星号和单个星号实际上是等价的，那么不连续的多个星号呢？
• 以 p=∗ abcd ∗ 为例，p 可以匹配所有包含子串 abcd 的字符串，也就是说，只需要暴力地枚举字符串 s 中的每个位置作为起始位置，并判断对应的子串是否为 abcd 即可。这种暴力方法的时间复杂度为 O(mn)，与动态规划一致，但不需要额外的空间。
• 如果 p=∗ abcd∗efgh∗i ∗ 呢？显然，p 可以匹配所有依次出现子串 abcd、efgh、i 的字符串。此时，对于任意一个字符串 s，首先暴力找到最早出现的 abcd，随后从下一个位置开始暴力找到最早出现的 efgh，最后找出 i，就可以判断 s 是否可以与 p 匹配。这样「贪心地」找到最早出现的子串是比较直观的，因为如果 s 中多次出现了某个子串，那么我们选择最早出现的位置，可以使得后续子串能被找到的机会更大。
• 因此，如果模式 p 的形式为 ∗ u₁ ∗ u₂ ∗ u₃ ∗⋯∗ u_x ∗，即字符串（可以为空）和星号交替出现，并且首尾字符均为星号，那么就可以设计出下面这个基于贪心的暴力匹配算法。算法的本质是：如果在字符串 s 中首先找到 u₁，再找到 u₂，u₃，u₄⋯ u_x，那么 s 就可以与模式 p 匹配，伪代码如下：

// 我们用 sIndex 和 pIndex 表示当前遍历到 s 和 p 的位置
// 此时我们正在 s 中寻找某个 u_i
// 其在 s 和 p 中的起始位置为 sRecord 和 pRecord

// sIndex 和 sRecord 的初始值为 0
// 即我们从字符串 s 的首位开始匹配
sIndex = sRecord = 0

// pIndex 和 pRecord 的初始值为 1
// 这是因为模式 p 的首位是星号，那么 u_1 的起始位置为 1
pIndex = pRecord = 1

while sIndex < s.length and pIndex < p.length do
    if p[pIndex] == '*' then
        // 如果遇到星号，说明找到了 u_i，开始寻找 u_i+1
        pIndex += 1
        // 记录下起始位置
        sRecord = sIndex
        pRecord = pIndex
    else if match(s[sIndex], p[pIndex]) then
        // 如果两个字符可以匹配，就继续寻找 u_i 的下一个字符
        sIndex += 1
        pIndex += 1
    else if sRecord + 1 < s.length then
        // 如果两个字符不匹配，那么需要重新寻找 u_i
        // 枚举下一个 s 中的起始位置
        sRecord += 1
        sIndex = sRecord
        pIndex = pRecord
    else
        // 如果不匹配并且下一个起始位置不存在，那么匹配失败
        return False
    end if
end while

// 由于 p 的最后一个字符是星号，那么 s 未匹配完，那么没有关系
// 但如果 p 没有匹配完，那么 p 剩余的字符必须都是星号
return all(p[pIndex] ~ p[p.length - 1] == '*')

• 然而模式 p 并不一定是 ∗ u₁ ∗ u₂ ∗ u₃ ∗⋯∗ u_x ∗ 的形式：
• • 模式 p 的开头字符不是星号；
• • 模式 p 的结尾字符不是星号。
• 第二种情况处理起来并不复杂，如果模式 p 的结尾字符不是星号，那么就必须与字符串 s 的结尾字符匹配。那么不断地匹配 s 和 p 的结尾字符，直到 p 为空或者 p 的结尾字符是星号为止。在这个过程中，如果匹配失败，或者最后 p 为空但 s 不为空，那么需要返回 False。
• 第一种情况的处理也很类似，我们可以不断地匹配 s 和 p 的开头字符。下面的代码中给出了另一种处理方法，即修改 sRecord 和 tRecord 的初始值为 −1，表示模式 p 的开头字符不是星号，并且在匹配失败时进行判断，如果它们的值仍然为 −1，说明没有「反悔」重新进行匹配的机会。
• C++ 示例：

class Solution 
public:
    bool isMatch(string s, string p) 
        auto allStars = [](const string& str, int left, int right) 
            for (int i = left; i < right; ++i) 
                if (str[i] != '*') 
                    return false;
                
            
            return true;
        ;
        auto charMatch = [](char u, char v) 
            return u == v || v == '?';
        ;

        while (s.size() && p.size() && p.back() != '*') 
            if (charMatch(s.back(), p.back())) 
                s.pop_back();
                p.pop_back();
            
            else 
                return false;
            
        
        if (p.empty()) 
            return s.empty();
        

        int sIndex = 0, pIndex = 0;
        int sRecord = -1, pRecord = -1;
        while (sIndex < s.size() && pIndex < p.size()) 
            if (p[pIndex] == '*') 
                ++pIndex;
                sRecord = sIndex;
                pRecord = pIndex;
            
            else if (charMatch(s[sIndex], p[pIndex])) 
                ++sIndex;
                ++pIndex;
            
            else if (sRecord != -1 && sRecord + 1 < s.size()) 
                ++sRecord;
                sIndex = sRecord;
                pIndex = pRecord;
            
            else 
                return false;
            
        
        return allStars(p, pIndex, p.size());
    
;

• Java 示例：

class Solution 
    public boolean isMatch(String s, String p) 
        int sRight = s.length(), pRight = p.length();
        while (sRight > 0 && pRight > 0 && p.charAt(pRight - 1) != '*') 
            if (charMatch(s.charAt(sRight - 1), p.charAt(pRight - 1))) 
                --sRight;
                --pRight;
             else 
                return false;
            
        

        if (pRight == 0) 
            return sRight == 0;
        

        int sIndex = 0, pIndex = 0;
        int sRecord = -1, pRecord = -1;
        
        while (sIndex < sRight && pIndex < pRight) 
            if (p.charAt(pIndex) == '*') 
                ++pIndex;
                sRecord = sIndex;
                pRecord = pIndex;
             else if (charMatch(s.charAt(sIndex), p.charAt(pIndex))) 
                ++sIndex;
                ++pIndex;
             else if (sRecord != -1 && sRecord + 1 < sRight) 
                ++sRecord;
                sIndex = sRecord;
                pIndex = pRecord;
             else 
                return false;
            
        

        return allStars(p, pIndex, pRight);
    

    public boolean allStars(String str, int left, int right) 
        for (int i = left; i < right; ++i) 
            if (str.charAt(i) != '*') 
                return false;
            
        
        return true;
    

    public boolean charMatch(char u, char v) 
        return u == v || v == '?';