机器学习Logistic回归详解（含源码）
Posted 大拨鼠
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习Logistic回归详解（含源码）相关的知识，希望对你有一定的参考价值。
作者：大拨鼠
注：本文相关练习用jupyter notebook完成，源文件可到公众号"大拨鼠Code"回复“机器学习”领取，题目及数据、文章的pdf版本都已打包在一起，如果对您有帮助，希望点个关注哦，万分感谢!
Logistic回归
文章目录
logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。
逻辑函数
我们将逻辑函数（sigmoid函数）定义为：
g ( z ) = 1 1 + e − z g(z)=\\frac11+e^-z g(z)=1+e−z1
由于 z = θ T x z=\\theta^Tx z=θTx也可以写为：
h θ ( x ) = 1 1 + e − θ T x h_\\theta(x)=\\frac11+e^-\\theta^Tx hθ(x)=1+e−θTx1
逻辑函数的图像如下：
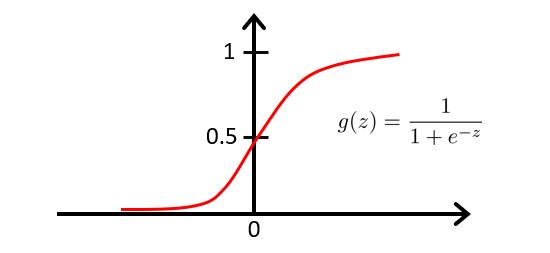
当有了 h θ ( x ) = 1 1 + e − θ T x h_\\theta(x)=\\frac11+e^-\\theta^Tx hθ(x)=1+e−θTx1这个函数后，我们要做的和前面线性回归时一样，就是用参数 θ \\theta θ去拟合我们的数据。
由于逻辑函数处于 0 − 1 0-1 0−1之间，且预测结果只输出1或者0，所以当 h θ ( x ) h_\\theta(x) hθ(x)为某个值时，这个值，代表的就是预测为1的概率，即当 h θ ( x ) = 0.7 h_\\theta(x)=0.7 hθ(x)=0.7时，以下为 y = 1 y=1 y=1和 y = 0 y=0 y=0的概率。
P ( y = 1 ∣ x , θ ) = 0.7 P(y=1|x,\\theta)=0.7 P(y=1∣x,θ)=0.7
P ( y = 0 ∣ x , θ ) = 1 − P ( y = 1 ∣ x , θ ) = 0.3 P(y=0|x,\\theta)=1-P(y=1|x,\\theta)=0.3 P(y=0∣x,θ)=1−P(y=1∣x,θ)=0.3
决策边界
我们现在来看看，逻辑函数什么时候会将 y y y预测为1，什么时候会预测为0
这时我们可以设定一个界限，例如我们设为0.5，则
h θ ( x ) ≥ 0.5 , y = 1 h_\\theta(x)≥0.5,y=1 hθ(x)≥0.5,y=1
h θ ( x ) < 0.5 , y = 0 h_\\theta(x)<0.5,y=0 hθ(x)<0.5,y=0
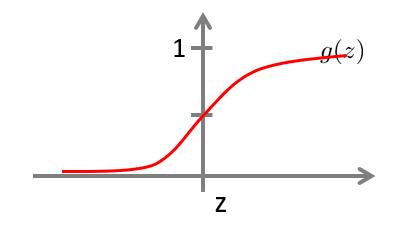
同时，又逻辑函数的图像可知：
当 z ≥ 0 时 ， h θ ( x ) ≥ 0.5 当z≥0时，h_\\theta(x)≥0.5 当z≥0时，hθ(x)≥0.5
当 z < 0 时 ， h θ ( x ) < 0.5 当z<0时，h_\\theta(x)<0.5 当z<0时，hθ(x)<0.5
现在假设我们有如下图所示的训练集和假设函数
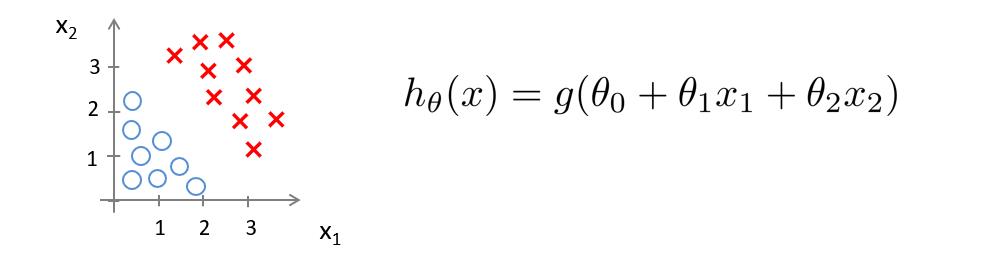
现在令 θ 0 = − 3 , θ 1 = 1 , θ 2 = 1 \\theta_0=-3,\\theta_1=1,\\theta_2=1 θ0=−3,θ1=1,θ2=1
则若是 − 3 + x 1 + x 2 ≥ 0 -3+x_1+x_2≥0 −3+x1+x2≥0，则预测 y = 1 y=1 y=1
我们知道， − 3 + x 1 + x 2 ≥ 0 -3+x_1+x_2≥0 −3+x1+x2≥0在图上表示的区域可以用提条直线划分
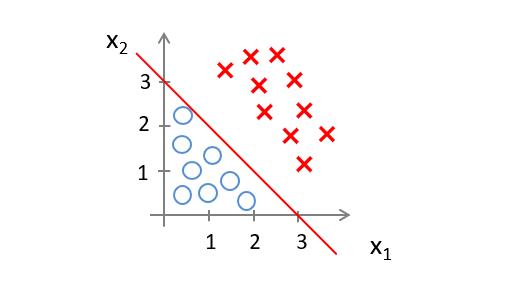
则当数据落在直线右边区域时，预测 y = 1 y=1 y=1，落在左边则预测 y = 0 y=0 y=0.
我们称这条线为决策边界，当 θ \\theta θ的值确定，我们的决策边界也随之确定。
下面再看个例子
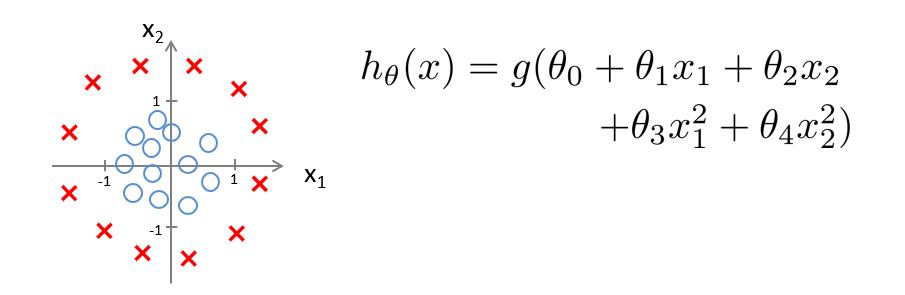
现在令 θ 0 = − 1 , θ 1 = 0 , θ 2 = 0 , θ 3 = 1 , θ 4 = 1 \\theta_0=-1,\\theta_1=0,\\theta_2=0,\\theta_3=1,\\theta_4=1 θ0=−1,θ1=0,θ2=0,θ3=1,θ4=1
则若是 − 1 + x 1 2 + x 2 2 ≥ 0 -1+x_1^2+x_2^2≥0 −1+x12+x22≥0，则预测 y = 1 y=1 y=1
此时的决策边界就是一个以0为原点，以1为半径的圆，但数据落在圆外，则预测 y = 1 y=1 y=1
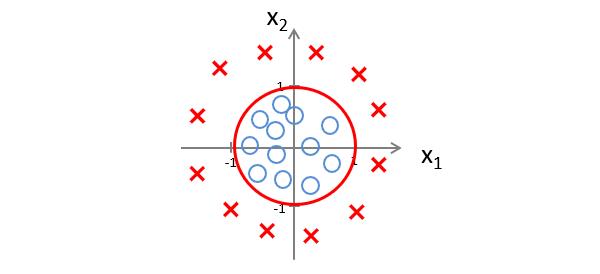
这里要在强调一下，我们不是用训练集去定义决策边界，而是用来拟合参数 θ \\theta θ，当 θ \\theta θ的值确定时，决策边界也就确定了。
代价函数
假设我们现在有n个特征值和m个训练样本的训练集
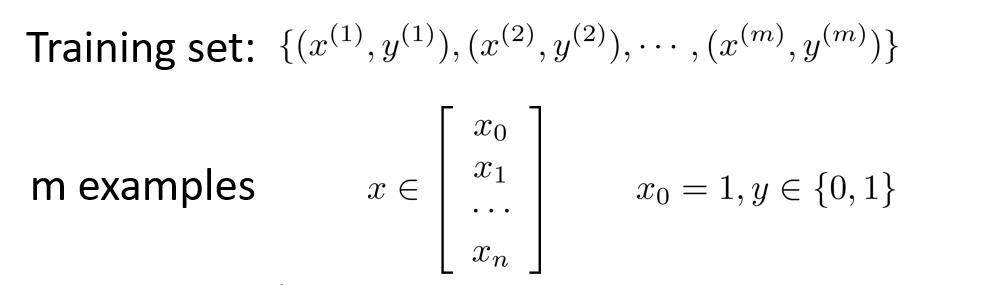
像之前线性回归一样，我们令 x 0 = 1 x_0=1 x0=1
我们假设函数：
h θ ( x ) = 1 1 + e − θ T x h_\\theta(x)=\\frac11+e^-\\theta^Tx hθ(x)=1+e−θTx1以上是关于机器学习Logistic回归详解（含源码）的主要内容，如果未能解决你的问题，请参考以下文章
logistic回归详解(二）：损失函数（cost function）详解
RF预测基于matlab随机森林算法数据回归预测含Matlab源码 2047期
RF预测基于matlab随机森林算法数据回归预测含Matlab源码 2047期