相似度/距离方法总结

Posted 2023-02-22 同学少年

假设两个向量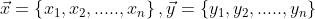

欧式距离：

                                                  

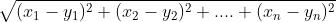
P范式：

p = 1, 1范式：

                                                       

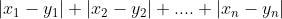
p = 2, 2范式（等于欧氏距离）：

                                                     

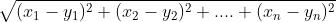
p = :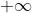

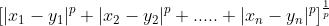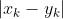                                      =  （前面里面最大的一项）

上面总称闵可夫斯基距离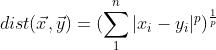                         

杰卡德相似系数：

                                                             

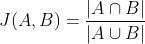
余弦相似度：

                                                                

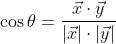
等于1时，方向相同，最相似，等于0时，方向垂直，-1时，方向相反，最不相似。

皮尔逊相关系数：

不认为x, y是两个n维的向量，而是两个随机变量，分别采样出n个值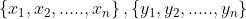，则可以计算出x的均值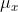, 标准差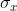,   y的均值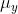, 标准差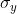.      x, y 的协方差记作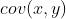, 则皮尔逊系数计算如下：

                                

                                                              = 

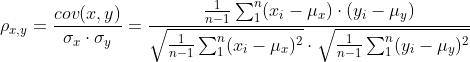
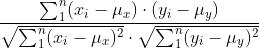
它的取值范围为[-1, 1], 值越大，越相关。

特殊情况下，当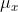 = 0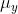，  = 0时，退化成了余弦相似度。

相对熵（K-L距离）

它是衡量两个分布的距离。

                                                    

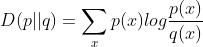
不具有对称性。非负。 分布完全相同时，相对熵为0， 分布差别越大，相对熵越大。