tslearn 笔记：dtw

Posted 2022-02-11 UQI-LIUWJ

1 介绍

        动态时间规整 (DTW) [1] 是时间序列之间的相似性度量。

DTW 笔记： Dynamic Time Warping 动态时间规整 （&DTW的python实现）_UQI-LIUWJ的博客-CSDN博客

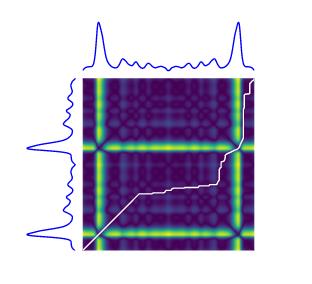
        让我们考虑两个时间序列 x=(x0,…,xn−1) 和 y=(y0,…,ym−1)，长度分别为 n 和 m。

        假设所有元素 xi 和 yj 位于相同的 d 维空间中。 在 tslearn 中，这样的时间序列将表示为各自形状 (n, d) 和 (m, d) 的数组，并且可以使用以下代码计算 DTW：

      注 tslearn中的dtw是开方后的结果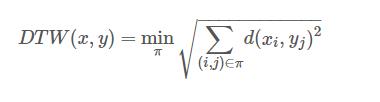  

 

 

from tslearn.utils import to_time_series
from tslearn.metrics import dtw, dtw_path

time_series_lst_1=to_time_series([1,3,5,7,9])
time_series_lst_2=to_time_series([2,4,6,8,0])

dtw_score = dtw(time_series_lst_1, time_series_lst_2)
dtw_score
#9.219544457292887

#如果两个时间序列之间是怎么相连的也很重要的话：
optimal_path, dtw_score_ = dtw_path(time_series_lst_1, time_series_lst_2)
optimal_path, dtw_score_ 
'''
([(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)], 9.219544457292887)
'''

2 使用自定义的距离函数

        默认情况下tslearn使用欧几里得距离作为两点之间的距离，如果我们要使用其他的距离函数，可以这么定义：

        

from tslearn.utils import to_time_series
from tslearn.metrics import dtw_path_from_metric

time_series_lst_1=to_time_series([1,3,5,7,9])
time_series_lst_2=to_time_series([2,4,6,8,0])

optimal_path, dtw_score_ = dtw_path_from_metric(
    time_series_lst_1, 
    time_series_lst_2,
    metric=lambda x,y :x+y)
optimal_path, dtw_score_
'''
([(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)], 45.0)
'''

3 其他一些对DTW的限制

可能会有很多条不同的路径，使得最终算出来的DTW值一样，于是后续论文研究了不同的限制条件 

3.1 Sakoe-Chiba 波段        

        Sakoe-Chiba 波段由半径 r 参数化（要考虑的非对角线元素的数量，有时也称为弯曲窗口大小warping window size），如下图所示：

from tslearn.utils import to_time_series
from tslearn.metrics import dtw

time_series_lst_1=to_time_series([1,3,5,7,9])
time_series_lst_2=to_time_series([2,4,6,8,0])

dtw_score_ = dtw(
    time_series_lst_1, 
    time_series_lst_2,
    global_constraint='sakoe_chiba',
    sakoe_chiba_radius=2)
dtw_score_
#9.219544457292887

 带path的同理

from tslearn.utils import to_time_series
from tslearn.metrics import dtw_path

time_series_lst_1=to_time_series([1,3,5,7,9])
time_series_lst_2=to_time_series([2,4,6,8,0])

optimal_path,dtw_score_ = dtw_path(
    time_series_lst_1, 
    time_series_lst_2,
    global_constraint='sakoe_chiba',
    sakoe_chiba_radius=2)
optimal_path,dtw_score_
'''
([(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)], 9.219544457292887)
'''

3.2  Itakura 平行四边形 

        Itakura 平行四边形为对齐路径设置了最大斜率 s，这导致了平行四边形约束：

from tslearn.utils import to_time_series
from tslearn.metrics import dtw_path

time_series_lst_1=to_time_series([1,3,5,7,9])
time_series_lst_2=to_time_series([2,4,6,8,0])

optimal_path,dtw_score_ = dtw_path(
    time_series_lst_1, 
    time_series_lst_2,
    global_constraint='itakura',
    itakura_max_slope=2)
optimal_path,dtw_score_
'''
([(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)], 9.219544457292887)
'''

3.3 soft-dtw

机器学习笔记 soft-DTW（论文笔记 A differentiable loss function for time-series）_UQI-LIUWJ的博客-CSDN博客

 

        由于min的不可微分性，DTW 就其输入而言不可微分。于是后来提出了一个可微扩展，其中 min 运算符被 soft-min 替换，使用 log-sum-exp 公式：  

max函数的平滑（log-sum-exp trick）_UQI-LIUWJ的博客-CSDN博客

        因此，soft-DTW 依赖于控制结果度量平滑的超参数 γ（DTW 结果的平方对应于极限情况 γ→0）。

 

from tslearn.utils import to_time_series
from tslearn.metrics import soft_dtw

time_series_lst_1=to_time_series([1,3,5,7,9])
time_series_lst_2=to_time_series([2,4,6,8,0])

soft_dtw_score_ = soft_dtw(
    time_series_lst_1, 
    time_series_lst_2,
    gamma=0.0001)
soft_dtw_score_
#85.0

'''
dtw 的resut，及其平方
(9.219544457292887, 85.0)
'''