利用MPI实现Cannon算法并行矩阵乘法
Posted 楚国令尹
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了利用MPI实现Cannon算法并行矩阵乘法相关的知识,希望对你有一定的参考价值。
C a n o n Canon\\, Canon算法是并行矩阵乘法的经典算法,将多个处理器排列成二维网格,采用二维块划分的方法将矩阵分给不同的处理器计算各自的局部结果,以此来加速计算。在本文中,为方便起见,示例程序中的矩阵均为 n n\\, n阶方阵,处理器的数量为2的幂次,确保每个矩阵得到的局部矩阵的元素个数相同。
一、二维矩阵串行乘法
两个
n
n\\,
n维方阵的乘法
A
×
B
=
C
A\\times B=C\\,
A×B=C的串行计算公式为:
C
i
j
=
∑
k
=
0
n
−
1
A
i
k
⋅
B
k
j
C_ij = \\sum_k=0^n-1 A_ik \\cdot B_kj
Cij=k=0∑n−1Aik⋅Bkj程序可以表示为:
void Multiply(double* A, double* B, double* C, int n)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
for (int k = 0; k < n; k++)
C[i * n + j] += A[i * n + k] * B[j + k * n];
程序将二维矩阵用一维矩阵线性展开,用一维数组来模拟二维数组。
二、Cannon算法
并行化二维矩阵乘法的一种思想是二维块划分方法,将
p
p\\,
p 个进程(
p
p\\,
p为完全平方数)排列成
p
×
p
\\sqrt[]p\\times\\sqrt[]p\\,
p×p二维网格,然后将矩阵
A
、
B
、
C
A、B、C\\,
A、B、C都分成
p
×
p
\\sqrt[]p\\times\\sqrt[]p\\,
p×p 块,均匀分布在网格上,矩阵第
(
i
,
j
)
(i,j)\\,
(i,j)个子块分别记为
A
i
j
A_ij\\,
Aij、
B
i
j
B_ij\\,
Bij、
C
i
j
C_ij\\,
Cij,存储在二维进程网格上坐标为
(
i
,
j
)
(i,j)\\,
(i,j)的进程
P
i
j
P_ij\\,
Pij上。计算
C
i
j
C_ij\\,
Cij时要将
A
i
k
A_ik\\,
Aik(第
i
i\\,
i行进程上的所有
A
A\\,
A的子块)和
B
k
j
B_kj\\,
Bkj(第
j
j\\,
j列进程上的所有
B
B\\,
B的子块)都收集到进程
P
i
j
P_ij\\,
Pij上,再计算
C
i
j
C_ij\\,
Cij,公式可以表达为:
C
i
j
=
∑
k
=
0
p
−
1
A
i
k
⋅
B
k
j
C_ij = \\sum_k=0^\\sqrt[]p-1 A_ik \\cdot B_kj
Cij=k=0∑p−1Aik⋅Bkj如下图所示:
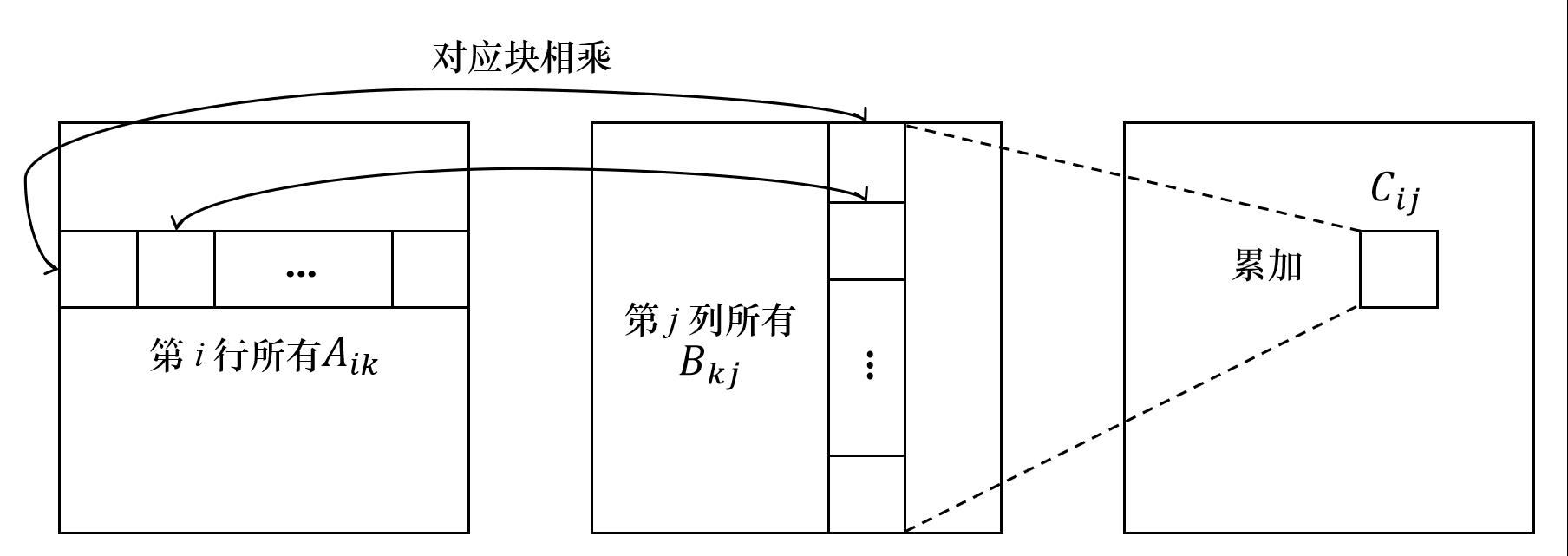
然而每一个进程都重复收集
A
i
k
A_ik\\,
Aik和
B
k
j
B_kj\\,
Bkj会造成空间的大量浪费,时间效率也比较低,于是有了更高效的
C
a
n
o
n
Canon\\,
Canon算法,其表达式为: 以上是关于利用MPI实现Cannon算法并行矩阵乘法的主要内容,如果未能解决你的问题,请参考以下文章
C
i
j
=
∑
k
=
0
p
−
1
A
i
,
(
i
+
j
+
k
)
%
p
⋅
B
(
i
+
j
+
k
)
%
p
,
j
C_ij = \\sum_k=0^\\sqrt[]p-1 A_i,(i+j+k)\\%\\sqrt[]p \\cdot B_(i+j+k)\\%\\sqrt[]p,j
Cij=k=0∑p−1Ai,(i+j+k)%p⋅B(i+j+k)%p,j
C
a
n
o
n
Canon\\,
Canon算法基本思想是,每一个进程只存储
A
A\\,
A、
B
B\\,
B、
C
C\\,
C矩阵的一个子块,本地相对应的
A
A\\,
A、
B
B\\,
B子块相乘后将结果累加到本地
C
C\\,
C子块上,然后再与其他进程交换
A
A\\,
A、
B
B\\,
B子块,继续相乘将结果累加到本地
C
C\\,
C子块上。但是要保证对应的
A
A\\,
A、
B
B\\,
B子块相乘,不能错位,我们注意到,在最开始,
P
i
j
P_ij\\,
Pij上的
A
A\\,
A为所在行的第
j
j\\,