LeetCode 剑指 Offer II 树（上） 专题总结

Posted 一只小逸白

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode 剑指 Offer II 树（上） 专题总结相关的知识，希望对你有一定的参考价值。

  • 📚 博客主页：⭐️这是一只小逸白的博客鸭~⭐️
  • 👉 欢迎 关注❤️点赞👍收藏⭐️评论📝
  • 😜 小逸白正在备战实习，经常更新面试题和LeetCode题解，欢迎志同道合的朋友互相交流~
  • 💙 若有问题请指正，记得关注哦，感谢~

树专题有点多，分成两篇博客发比较方便阅读复习

往期文章 ：

目录

047. 二叉树剪枝

题目：

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。
节点 node 的子树为 node 本身，以及所有 node 的后代。

示例：

输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]
解释:
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案

提示:

  • 二叉树的节点个数的范围是 [1,200]
  • 二叉树节点的值只会是 0 或 1

思路

后序遍历二叉树
遍历左右子树，若两边都为Null 且自己本身为0，则删除自己，返回Null给父节点

class Solution 
public:
    TreeNode* pruneTree(TreeNode* root) 
        return dfs(root);
    
    //后序遍历，left -> right -> root
    TreeNode* dfs(TreeNode* root) 
        if(root == nullptr)
            return nullptr;

        //遍历左子树
        root->left = dfs(root->left);
        //遍历右子树
        root->right = dfs(root->right);
        //节点为0且是叶子结点就返回nullprt删除本节点
        if(root->val == 0 && !root->right && !root->left) 
            return nullptr;
        else 
            //否则返回原本的树
            return root;
        
    
;

048. 序列化与反序列化二叉树（困难）

题目：

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例：


输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

提示：

  • 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，也可以采用其他的方法解决这个问题。
  • 树中结点数在范围 [0, 104] 内
  • -1000 <= Node.val <= 1000

思路

字符串格式好像可以由自己设置，也可以参考提示LeetCode官方的格式：
string： "1,2,3,#,4" --------- TreeNode： ["1","2","3"","#","4"]

  • 序列化serialize ：前序遍历 根->左->右，为null转为"#"，然后就是"root, root->left, root->right"格式添加字符串
  • 反序列化deserialize：1. 分割字符串， 2. 前序遍历将字符串转换成二叉树
class Codec 
public:

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) 
        if(root == nullptr) 
            return "#";
        
        string left = serialize(root->left);
        string right = serialize(root->right);
        //字符串形式为 "1,2,3,#,4"
        return to_string(root->val) + "," + left + "," + right;
    

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) 
        //分割字符串 "1,2,3,#,4" -> ["1","2","3"","#","4"];
        vector<string> dataArray;
        //第一个字符串的开头，添加空字符串是为了数字不只一个，需一个一个加入数组的字符串中
        dataArray.push_back("");
        for(auto& ch : data) 
            if(ch == ',') 
                //在数组最后面添加一个空字符串，表示该该位数组的开头
                dataArray.push_back("");
            else 
                //数字不只一个字符ch，而是字符串，在数组的最后一个字符串每次加一个数组的字符
                dataArray.back().push_back(ch);
            
        
        int index = 0;
        return dfs(dataArray, index);
    
    // index记得使用引用，访问一个增加一次，在return null之前，否则无法顺利访问数组
    TreeNode* dfs(vector<string>& strs, int& index) 
        string str = strs[index++];
        if(str == "#") 
            return nullptr;
        
        TreeNode* node = new TreeNode(stoi(str));
        //index重点！！！必须这样，不然遇到空就不好访问数组
        node->left = dfs(strs, index);
        node->right = dfs(strs, index);
        return node;
    

;

049. 从根节点到叶节点的路径数字之和

题目：

给定一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

  • 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。

示例：


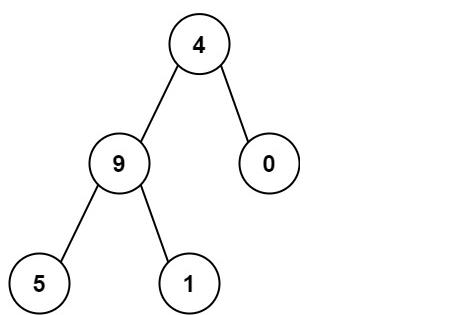
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

  • 树中节点的数目在范围 [1, 1000] 内
  • 0 <= Node.val <= 9
  • 树的深度不超过 10

思路

前序遍历

  1. 计算本节点的值 --> 上一节点 * 10 + 本节点
  2. 如果是叶子节点就直接返回该路径值
  3. 否则不是叶子节点，继续向下，并且将左右子树节点和返回
class Solution 
public:
    int sumNumbers(TreeNode* root) 
        return dfs(root, 0);;
    
    int dfs(TreeNode* root, int ans) 
        if(root == nullptr) return 0;
        //当前节点表示的数 
        ans = ans * 10 + root->val;
        //如果为叶子节点就返回本节点的值
        if(root->left == nullptr && root->right == nullptr) 
            return ans;
        else 
            //不是叶子节点就返回左右子树的和
            return dfs(root->left, ans) + dfs(root->right, ans);
        
    
;

050. 向下的路径节点之和

题目：

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例：


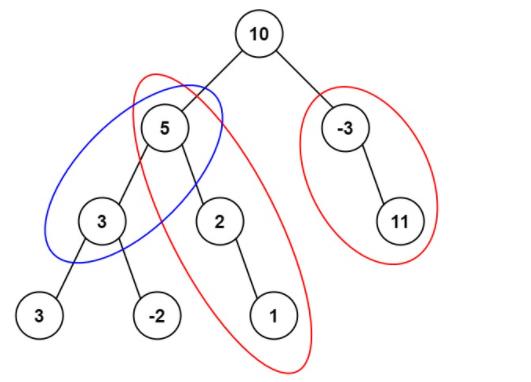
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

提示:

  • 二叉树的节点个数的范围是 [0,1000]
  • -109 <= Node.val <= 109
  • -1000 <= targetSum <= 1000

思路

做这题之前先把 剑指 Offer II 010. 和为 k 的子数组 这题做会了就简单了。
这题就是 前缀和 + 回溯 + map
运用前缀和思想，求每一条路径的中间某一段路径和为 targetSum 的子路径
用map方便快速寻找路径和为 sum - targetSum 的路径
若存在表示当前路径总和减去起点到某一节点和（前半部分）为 sum - targetSum = 后半部分路径targetSum

class Solution 
public:

    //剑指 Offer II 010. 和为 k 的子数组 这道题的扩展 前缀和
    //将根节点到叶子结点的路径想象成 子数组， 运用010题的思路求解
    unordered_map<int, int> map;
    int pathSum(TreeNode* root, int targetSum) 
        map[0] = 1;
        return dfs(root, targetSum, 0);
    

    int dfs(TreeNode* root, int targetSum, int sum) 
        if(root == nullptr) return 0;

        sum += root->val;
        //代表从当前节点到前面某一节点的路径，某一节点前面的和在此前已经存入map
        int count = map[sum - targetSum];
        map[sum]++;

        count += dfs(root->left, targetSum, sum) + dfs(root->right, targetSum, sum);
        //回溯，要退回到本节点的上一层，所以不包含 map[sum]
        map[sum]--;
        return count;
    
;

051. 节点之和最大的路径（困难）

题目：

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给定一个二叉树的根节点 root ，返回其 最大路径和，即所有路径上节点值之和的最大值。

示例：


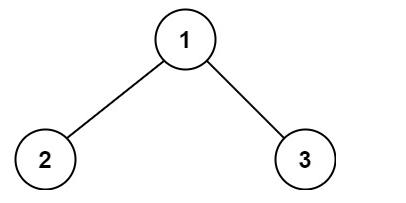
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

提示：

  • 树中节点数目范围是 [1, 3 * 104]
  • -1000 <= Node.val <= 1000

思路

后序遍历

  • ans 用于返回当前节点能够返回给父节点的最大路径
  • rootMax 用于计算已当前节点为答案节点，计算左右子树加上节点值的最大值
  • 上面两个都要考虑如果左子树或者右子树返回负值就不取
class Solution 
public:
    int res = -1000;
    int maxPathSum(TreeNode* root) 
        dfs(root);
        return res;
    
    int dfs(TreeNode* root) 
        if(root == nullptr) return 0;
        int left = dfs(root->left);
        int right = dfs(root->right);
        //取本节点能够达到的最大的路径  --> 这是条单路径，两边最多取一个或者不取
        int ans = root->val;
        //左右子树有个大于0才进行取最大值， 否则取本身值就是目前最大值
        if(left > 0 || right > 0)
           ans += max(left, right);
         
        //本节点为答案所能连接成的最大路径， --> 本节点加上左右子树的和 
        int rootMax = root->val;
        //左右子树大于0才加上， 否则取本身值就是目前最大值
        if(left > 0) rootMax += left;
        if(right > 0) rootMax += right;
        //存储最大值
        res = max(res, rootMax);
        return ans;
    
;

052. 展平二叉搜索树

题目：

给你一棵二叉搜索树，请 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

示例：


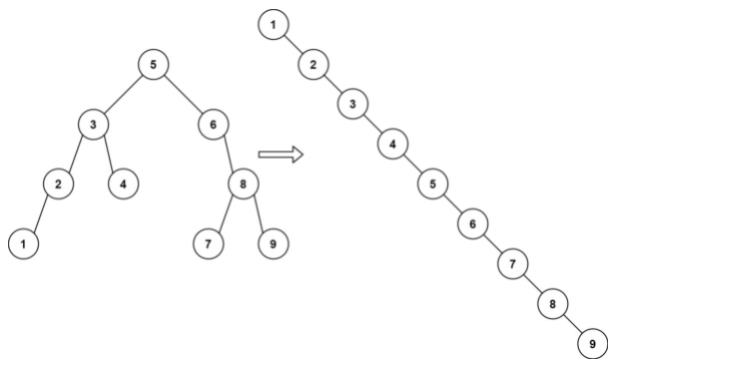
输入：root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出：[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

提示：

  • 树中节点数的取值范围是 [1, 100]
  • 0 <= Node.val <= 1000

思路

创建一个头结点（哨兵），中序遍历连接所有节点
重点：记得将遍历的所有节点的左节点置null，特别是最后一个，如果左节点指向第一个节点就形成环

class Solution 
public:
    TreeNode* curNode;
    TreeNode* increasingBST(TreeNode* root) 
        TreeNode* dummy = new TreeNode(-1);
        curNode = dummy;
        dfs(root);
        return dummy->right;
    
    void dfs(TreeNode* root) 
        if(root == nullptr) return ;
        //左
        dfs(root->left);
        //中
        curNode->right = root;
        //每次将遍历到的节点左子树置空，防止有左子树形成循环
        root->left = nullptr;
        curNode = root;
        //右
        dfs(root->right);
    
;

以上是关于LeetCode 剑指 Offer II 树（上） 专题总结的主要内容，如果未能解决你的问题，请参考以下文章

leetcode-剑指 Offer 55 - II平衡二叉树

算法leetcode剑指 Offer II 045. 二叉树最底层最左边的值（rust和go重拳出击）

算法leetcode剑指 Offer II 045. 二叉树最底层最左边的值（rust和go重拳出击）

Leetcode二叉树专题(仅需7道题就可以带你入门二叉树基本玩法)

剑指offer树55-II.平衡二叉树

剑指offer树55-II.平衡二叉树